Hostname: page-component-5cf477f64f-54txb Total loading time: 0 Render date: 2025-04-04T04:23:53.570Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-modal perturbation growth in a laminar jet: an experimental study

Published online by Cambridge University Press:  15 May 2023

O.O. Ivanov Open the ORCID record for O.O. Ivanov [Opens in a new window] ,
D.A. Ashurov ,
L.R. Gareev Open the ORCID record for L.R. Gareev [Opens in a new window]  and
V.V. Vedeneev Open the ORCID record for V.V. Vedeneev [Opens in a new window]
O.O. Ivanov*
Affiliation:
Institute of Mechanics, Lomonosov Moscow State University, Moscow 119192, Russia
D.A. Ashurov
Affiliation:
Institute of Mechanics, Lomonosov Moscow State University, Moscow 119192, Russia Department of Mechanics and Mathematics, Lomonosov Moscow State University, Moscow 119991, Russia
L.R. Gareev
Affiliation:
Institute of Mechanics, Lomonosov Moscow State University, Moscow 119192, Russia Department of Mechanics and Mathematics, Lomonosov Moscow State University, Moscow 119991, Russia
V.V. Vedeneev
Affiliation:
Institute of Mechanics, Lomonosov Moscow State University, Moscow 119192, Russia Department of Mechanics and Mathematics, Lomonosov Moscow State University, Moscow 119991, Russia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

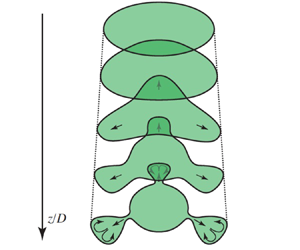
It is known that, apart from the growth of instability modes, the non-modal (algebraic) mechanism of linear growth plays an important role in near-wall flows. In unbounded flows, including submerged jets, the theoretical analysis of the non-modal growth mechanism started only in the last decade; this mechanism has not yet been identified in experiments. In the present work, experiments were conducted on the excitation of a non-modal ‘lift-up’ growth mechanism. Special wavy structures (deflectors) were introduced into a laminar round submerged jet, which excited a roller-like transverse motion. Based on experimental results, we definitely identify the non-modal ‘lift-up’ growth mechanism of introduced disturbances. The development of perturbations in the experiment qualitatively corresponds to the theoretically calculated optimal perturbations. The features of the transition to turbulence caused by non-modal growth are considered.

JFM classification

Instability: Shear-flow instability Wakes/Jets: Jets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 963 , 25 May 2023 , A8
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersson, P., Berggren, M. & Henningson, D.S. 1999 Optimal disturbances and bypass transition in boundary layers. Phys. Fluids 11, 134–150.CrossRefGoogle Scholar
Boiko, A.V., Grek, G.R., Dovgal, A.V. & Kozlov, V.V. 2002 The Origin of Turbulence in Near-Wall Flows. Springer.CrossRefGoogle Scholar
Boronin, S.A., Healey, J.J. & Sazhin, S.S. 2013 Non-modal stabillity of round viscous jets. J. Fluid Mech. 716, 96–119.CrossRefGoogle Scholar
Butler, K.M. & Farrell, B.F. 1992 Three-dimensional optimal perturbations in viscous shear flow. Phys. Fluids A: Fluid Dyn. 4, 1637–1650.CrossRefGoogle Scholar
Canuto, C., Hussaini, M.Y., Quarteroni, A. & Zang, T.A. 2007 Spectral Methods. Springer.CrossRefGoogle Scholar
Ellingsen, T. & Palm, E. 1975 Stability of linear flow. Phys. Fluids 18, 487–488.CrossRefGoogle Scholar
Farrell, B.F. & Ioannou, P.J. 1993 Stochastic forcing of the linearized Navier–Stokes equations. Phys. Fluids A: Fluid Dyn. 5, 2600–2609.CrossRefGoogle Scholar
Fransson, J.H.M., Matsubara, M. & Alfredsson, P.H. 2005 Transition induced by free-stream turbulence. J. Fluid Mech. 527, 1–25.CrossRefGoogle Scholar
Gareev, L.R., Zayko, J.S., Chicherina, A.D., Trifonov, V.V., Reshmin, A.I. & Vedeneev, V.V. 2022 Experimental validation of inviscid linear stability theory applied to an axisymmetric jet. J. Fluid Mech. 934, A3.CrossRefGoogle Scholar
Grek, G.R., Katasonov, M.M. & Kozlov, V.V. 2008 Modelling of streaky structures and turbulent-spot generation process in wing boundary layer at high free-stream turbulence. Thermophys. Aeromech. 15, 549–561.CrossRefGoogle Scholar
Jiménez-González, J.I. & Brancher, P. 2017 Transient energy growth of optimal streaks in parallel round jets. Phys. Fluids 29, 114101.CrossRefGoogle Scholar
Jiménez-González, J.I., Brancher, P. & Martínez-Bazán, C. 2015 Modal and non-modal evolution of perturbations for parallel round jets. Phys. Fluids 27, 044105.CrossRefGoogle Scholar
Kendall, J.M. 1985 Experimental study of disturbances produced in a pre-transitional laminar boundary layer by weak free stream turbulence. In 18th Fluid Dynamics and Plasmadynamics and Lasers Conference. AIAA.CrossRefGoogle Scholar
Khorrami, M.R., Malik, M.R. & Ash, R.L. 1989 Application of spectral collocation techniques to the stability of swirling flows. J. Comput. Phys. 81 (1), 206–229.CrossRefGoogle Scholar
Kosorygin, V.S., Polyakov, N.F., Suprun, T.T. & Epic, E.Y. 1984 Influence of turbulence on the structure of perturbations in a laminar boundary layer. In Pristenochnyiye turbulentnyiye techeniya, pp. 79–83. Institute of Thermophysics of the Siberian Branch of the USSR Academy of Sciences (in Russian).Google Scholar
Kozlov, V.V., Grek, G.R., Lofdahl, L.L., Chernorai, V.G. & Litvinenko, M.V. 2002 Role of localized streamwise structures in the process of transition to turbulence in boundary layers and jets (review). J. Appl. Mech. Tech. Phys. 43, 224–236.CrossRefGoogle Scholar
Landahl, M.T. 1980 A note on an algebraic instability of inviscid parallel shear flows. J. Fluid Mech. 98, 243–251.CrossRefGoogle Scholar
Liepmann, D. & Gharib, M. 1992 The role of streamwise vorticity in the near-field entrainment of round jets. J. Fluid Mech. 245, 643–668.CrossRefGoogle Scholar
Luchini, P. 2000 Reynolds-number-independent instability of the boundary layer over a flat surface: optimal perturbations. J. Fluid Mech. 404, 289–309.CrossRefGoogle Scholar
Marant, M. & Cossu, C. 2018 Influence of optimally amplified streamwise streaks on the Kelvin–Helmholtz instability. J. Fluid Mech. 838, 478–500.CrossRefGoogle Scholar
Matsubara, M. & Alfredsson, P.H. 2001 Disturbance growth in boundary layers subjected to free-stream turbulence. J. Fluid Mech. 430, 149–168.CrossRefGoogle Scholar
Morkovin, M.V. 1984 Bypass transition to turbulence and research desiderata. NASA Conf. Publ. 2386, 161.Google Scholar
Nastro, G., Fontane, J. & Joly, L. 2020 Optimal perturbations in viscous round jets subject to Kelvin–Helmholtz instability. J. Fluid Mech. 900, A13.CrossRefGoogle Scholar
Reshotko, E. & Tumin, A. 2001 Spatial theory of optimal disturbances in a circular pipe flow. Phys. Fluids 13, 991–996.CrossRefGoogle Scholar
Schlichting, G. 1979 Boundary Layer Theory. McGraw-Hill.Google Scholar
Schmid, P.J. & Henningson, D.S. 1994 Optimal energy density growth in Hagen–Poiseuille flow. J. Fluid Mech. 277, 197–225.CrossRefGoogle Scholar
Schmid, P.J. & Henningson, D.S. 2001 Stability and Transition in Shear Flows. Springer.CrossRefGoogle Scholar
Shahinfar, S., Sattarzadeh, S.S. & Fransson, J.H.M. 2014 Passive boundary layer control of oblique disturbances by finite-amplitude streaks. J. Fluid Mech. 749, 1–36.CrossRefGoogle Scholar
Trefethen, L.N. 2000 Spectral Methods in MATLAB. SIAM.CrossRefGoogle Scholar
Tumin, A. & Reshotko, E. 2001 Spatial theory of optimal disturbances in boundary layers. Phys. Fluids 13, 2097–2104.CrossRefGoogle Scholar
Wang, C., Lesshafft, L., Cavalieri, A.V. & Jordan, P. 2021 The effect of streaks on the instability of jets. J. Fluid Mech. 910, A14.CrossRefGoogle Scholar
Westin, K.J.A., Boiko, A.V., Klingmann, B.G.B., Kozlov, V.V. & Alfredsson, P.H. 2001 Disturbance growth in boundary layers subjected to free-stream turbulence. J. Fluid Mech. 430, 149–168.Google Scholar
Zayko, J., Teplovodskii, S., Chicherina, A., Vedeneev, V. & Reshmin, A. 2018 Formation of free round jets with long laminar regions at large Reynolds numbers. Phys. Fluids 30, 043603.CrossRefGoogle Scholar