Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T06:28:39.893Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear stability, bifurcation and vortical patterns in three-dimensional granular plane Couette flow

Published online by Cambridge University Press:  25 January 2013

Meheboob Alam  and
Priyanka Shukla
Meheboob Alam*
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur P.O., Bangalore 560064, India
Priyanka Shukla
Affiliation:
Department of Mathematics and Statistics, Indian Institute of Science Education and Research Kolkata, P.O.: BCKV Campus, Mohanpur, Nadia 741252, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The effects of three-dimensional (3D) perturbations, having wave-like modulations along both the streamwise and spanwise/vorticity directions, on the nonlinear states of five types of linear instability modes, the nature of their bifurcations and the resulting nonlinear patterns are analysed for granular plane Couette flow using an order-parameter theory which is an extension of our previous work on two-dimensional (2D) perturbations (Shukla & Alam, J. Fluid Mech., vol. 672, 2011b, pp. 147–195). The differential equations for modal amplitudes (the fundamental mode, the mean-flow distortion, the second harmonic and the distortion of the fundamental mode), up to cubic-order in perturbation amplitude, are solved using a spectral-based numerical technique, yielding an estimate of the first Landau coefficient that accounts for the leading-order nonlinear effect on finite-amplitude perturbations. In the near-critical regime of flows, we found evidence of mean-flow resonance, characterized by the divergence of the first Landau coefficient, that occurs due to the interaction/resonance between a linear instability mode and a mean-flow mode. The nonlinear solutions are found to appear via both pitchfork and Hopf bifurcations from the underlying linear instability modes, leading to supercritical nonlinear states of stationary and travelling wave solutions. The subcritical travelling wave solutions have also been uncovered in the linearly stable regimes of flow. It is shown that multiple nonlinear states of both stationary and travelling waves can coexist for a given parameter combination of mean density and Couette gap. The 3D nonlinear solutions persist for a range of spanwise wavenumbers up to 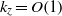${k}_{z} = O(1)$ that originate from 2D instabilities which occur beyond a moderate value of the mean density. For purely 3D instabilities in dilute flows (having no analogue in 2D flows), the supercritical finite-amplitude solutions persist for a much larger range of spanwise wavenumber up to 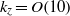${k}_{z} = O(10)$. For all instabilities, the vortical motion on the cross-stream plane has been characterized in terms of the fixed/critical points of the underlying flow field: saddles, nodes (sources and sinks) and vortices have been identified. While the cross-stream velocity field for supercritical solutions in dilute flows contains nodes and saddles, the subcritical solutions are dominated by large-scale vortices in the background of saddle-node-type motions. The latter type of flow pattern also persists at moderate densities in the form of supercritical nonlinear solutions that originate from the dominant 2D instability modes for which the vortex appears to be driven by two nearby saddles. The location of this vortex is found to be correlated with the local maxima of the streamwise vorticity.

JFM classification

Granular media: Granular media Instability: Nonlinear instability Nonlinear Dynamical Systems: Pattern formation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 716 , 10 February 2013 , pp. 349 - 413
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alam, M. 2005 Universal unfolding of pitchfork bifurcations and the shear-band formation in rapid granular Couette flow. In Trends in Applications of Mathematics to Mechanics (ed. Wang, Y. & Hutter, K.), pp. 11–20. Shaker.Google Scholar
Alam, M. 2006 Streamwise structures and density patterns in rapid granular Couette flow: a linear stability analysis. J. Fluid Mech. 553, 1.Google Scholar
Alam, M., Arakeri, V. H., Goddard, J. D., Nott, P. R. & Herrmann, H. J. 2005 Instability-induced ordering, universal unfolding and the role of gravity in granular Couette flow. J. Fluid Mech. 523, 277.Google Scholar
Alam, M., Chikkadi, V. K. & Gupta, V. K. 2009 Density waves and the effect of wall roughness in granular Poiseuille flow: simulation and linear stability. Eur. Phys. J. ST 179, 69.Google Scholar
Alam, M. & Luding, S. 2003 First normal stress difference and crystallization in a dense sheared granular fluid. Phys. Fluids 15, 2298.Google Scholar
Alam, M. & Luding, S. 2005 Energy nonequipartition, rheology and microstructure in sheared bidisperse granular mixtures. Phys. Fluids 17, 063303.CrossRefGoogle Scholar
Alam, M. & Nott, P. R. 1998 Stability of plane Couette flow of a granular material. J. Fluid Mech. 377, 99.CrossRefGoogle Scholar
Alam, M. & Shukla, P. 2008 Nonlinear stability of granular shear flow: Landau equation, shear-banding and universality. In Proceedings of International Conference on Theoretical and Applied Mechanics (ISBN 978-0-9805142-0-9), 24–29 August, Adelaide, Australia.Google Scholar
Alam, M. & Shukla, P. 2012 Origin of subcritical shear-banding instability in a dense two-dimensional sheared granular fluid. Gran. Matt. 14, 221.Google Scholar
Alam, M., Shukla, P. & Luding, S. 2008 Universality of shear-banding instability and crystallization in sheared granular fluid. J. Fluid Mech. 615, 293.CrossRefGoogle Scholar
Aranson, I. S. & Tsimring, L. S. 2006 Patterns and collective behaviour in granular media: theoretical concepts. Rev. Mod. Phys. 78, 641.Google Scholar
Brilliantov, N. V. & Pöschel, T. 2004 Kinetic Theory of Granular Gases. Oxford University Press.Google Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 1988 Spectral Methods in Fluid Dynamics. Springer.Google Scholar
Carr, J. 1981 Applications of Center Manifold Theory. Springer.CrossRefGoogle Scholar
Chikkadi, V. K. & Alam, M. 2009 Slip velocity and stresses in granular Poiseuille flow via event-driven simulation. Phys. Rev. E 79, 021303.CrossRefGoogle Scholar
Chong, M. S., Perry, A. E. & Cantwell, B. J. 1990 A general classification of three-dimensional flow fields. Phys. Fluids A 2, 765.Google Scholar
Conway, S. & Glasser, B. J. 2004 Density waves and coherent structures in granular Couette flow. Phys. Fluids 16, 509.CrossRefGoogle Scholar
Cross, M. C. & Hohenberg, P. 1993 Patterns formation outside of equilibrium. Rev. Mod. Phys. 65, 851.Google Scholar
Drazin, P. G. 1992 Nonlinear Systems. Cambridge University Press.CrossRefGoogle Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Eckhaus, W. 1965 Studies in Nonlinear Stability Theory. Cambridge University Press.Google Scholar
Eshuis, P., van der Meer, D., Alam, M., van Gerner, H. J., van der Weele, K. & Lohse, D. 2010 Onset of convection in strongly shaken granular matter. Phys. Rev. Lett. 104, 038001.CrossRefGoogle ScholarPubMed
Forterre, F. & Pouliquen, O. 2002 Stability analysis of rapid granular chute flows: formation of longitudinal vortices. J. Fluid Mech. 467, 361.Google Scholar
Gallas, J. A . C., Herrmann, H. J. & Sokolowski, S. 1992 Convection cells in vibrating granular layers. Phys. Rev. Lett. 69, 1371.Google Scholar
Garzo, V. & Dufty, J. W. 1999 Dense fluid transport for inelastic hard spheres. Phys. Rev. E 59, 5895.Google Scholar
Garzo, V., Santos, A. & Montanero, J. M. 2007 Modified Sonine approximation for the Navier–Stokes transport coefficients of a granular gas. Physica A 376, 94.Google Scholar
Gayen, B. & Alam, M. 2006 Algebraic and exponential instabilities in a sheared micropolar granular fluid. J. Fluid Mech. 567, 195.Google Scholar
Goddard, J. D. & Alam, M. 1999 Shear flow and material instabilities in particulate suspensions and dry granular media. Particulate Sci. Tech. 17, 69.Google Scholar
Goldfarb, D. J., Glasser, B. J. & Shinbrot, T. 2002 Shear instabilities in granular flows. Nature 415, 302.CrossRefGoogle ScholarPubMed
Goldhirsch, I. 2003 Rapid granular flows. Annu. Rev. Fluid Mech. 35, 267.CrossRefGoogle Scholar
Hopkins, M. A., Jenkins, J. T. & Louge, M. Y. 1993 On the structure of three-dimensional shear flows. In Advances in Micromechanics of Granular Materials (ed. Shen, H. H., Satake, M., Mehrabadi, M., Chang, C. S. & Campbell, C. S.), pp. 271–279. Elsevier.Google Scholar
Jackson, R. 2000 Dynamics of Fluidized Beds. Cambridge University Press.Google Scholar
Jenkins, J. T. & Richman, M. W. 1985 Grads 13-moment system for a dense gas of inelastic spheres. Arch. Rat. Mech. Anal. 87, 355.Google Scholar
Jenkins, J. T. & Richman, M. W. 1986 Boundary conditions for plane flows of smooth, nearly elastic, circular disks. J. Fluid Mech. 171, 53.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69.CrossRefGoogle Scholar
Khain, E. & Meerson, B. 2006 Shear-induced crystallization of a dense rapid granular flow: hydrodynamics beyond the melting point. Phys. Rev. E 73, 061301.Google Scholar
Lun, C. K. K., Savage, S. B., Jeffrey, D. J. & Chepurniy, N. 1984 Kinetic theories for granular flow: inelastic particles in Couette flow and slightly inelastic particles in a general flow field. J. Fluid Mech. 140, 223.CrossRefGoogle Scholar
Mack, L. M. 1984 Boundary layer linear stability theory. AGARD Rep. 709, p. 3-1.Google Scholar
Malik, M., Alam, M. & Dey, J. 2006 Nonmodal energy growth and optimal perturbations in compressible Couette flow. Phys. Fluids 18, 034103.CrossRefGoogle Scholar
Malik, M., Dey, J. & Alam, M. 2008 Linear stability, transient energy growth and the role of viscosity stratification in compressible plane Couette flow. Phys. Rev. E 77, 036322.Google Scholar
McNamara, S. 1993 Hydrodynamic modes of a uniform granular medium. Phys. Fluids A 5, 3056.Google Scholar
Morozov, A. N. & van Saarloos, W. 2007 An introductory essay on subcritical instabilities and the transition to turbulence in visco-elastic parallel shear flows. Phys. Rep. 447, 112.Google Scholar
Noskowicz, S. H., Bar-Lev, O., Serero, D. & Goldhirsch, I. 2007 Computer-aided kinetic theory and granular gases. Europhys. Lett. 79, 60001.Google Scholar
Perry, A. E. & Chong, M. S. 1987 A description of eddying motions and flow patterns using critical-point concepts. Annu. Rev. Fluid Mech. 19, 125.CrossRefGoogle Scholar
Raafat, T., Hulin, J. P. & Herrmann, H. J. 1996 Density waves in dry granular media falling through a vertical pipe. Phys. Rev. E 53, 4345.Google Scholar
Ramirez, R., Risso, D. & Cordero, P. 2000 Thermal convection in fluidized granular systems. Phys. Rev. Lett. 85, 1030.Google Scholar
Reynolds, W. C. & Potter, M. C. 1967 Finite amplitude instability of parallel shear flows. J. Fluid Mech. 27, 465.Google Scholar
Saitoh, K. & Hayakawa, H. 2007 Rheology of a granular gas under a plane shear. Phys. Rev. E 75, 021302.Google Scholar
Saitoh, K. & Hayakawa, H. 2011 Weakly nonlinear analysis of two-dimensional sheared granular flow. Granul. Matt. 13, 679.Google Scholar
Sauermann, G., Kroy, K. & Herrmann, H. J. 2001 A continuum saltation model for sand dunes. Phys. Rev. E 64, 031305.Google Scholar
Savage, S. B. 1992 Instability of unbounded uniform granular shear flow. J. Fluid Mech. 241, 109.Google Scholar
Sela, N. & Goldhirsch, I. 1998 Hydrodynamic equations for rapid shear flows of smooth, inelastic spheres, to Burnett order. J. Fluid Mech. 361, 41.Google Scholar
Shukla, P. & Alam, M. 2009 Order parameter description of shear-banding in granular Couette flow via Landau equation. Phys. Rev. Lett. 103, 068001.Google Scholar
Shukla, P. & Alam, M. 2011a Weakly nonlinear theory of shear-banding instability in granular plane Couette flow: analytical solution, comparison with numerics and bifurcation. J. Fluid Mech. 666, 204.Google Scholar
Shukla, P. & Alam, M. 2011b Nonlinear stability and patterns in granular plane Couette flow: Hopf and pitchfork bifurcations, and evidence for resonance. J. Fluid Mech. 672, 147.Google Scholar
Shukla, P. & Alam, M. 2012 Nonlinear vorticity banding instability in granular plane Couette flow: higher-order Landau coefficient, bistability and bifurcation scenario. J. Fluid Mech. (in press).Google Scholar
Stuart, J. T. 1960 On the nonlinear mechanics of wave disturbances in stable and unstable parallel flows. J. Fluid Mech. 9, 353.Google Scholar
Tan, M.-L. & Goldhirsch, I. 1997 Inter-cluster interactions in rapid granular shear flows. Phys. Fluids 9, 856.Google Scholar
Trefethen, N. & Bau, H. 1997 Linear Algebra. SIAM.Google Scholar
Umbanhower, P., Melo, F. & Swinney, H. L. 1996 Oscillons in vibrated granular media. Nature 382, 793.Google Scholar
Watson, J. 1960 On the nonlinear mechanics of wave disturbances in stable and unstable parallel flows. J. Fluid Mech. 9, 371.CrossRefGoogle Scholar
Woodhouse, M. J. & Hogg, A. J. 2010 Rapid granular flows down inclined planar chutes. Part 2. Linear stability analysis of steady flow solutions. J. Fluid Mech. 652, 461.Google Scholar