Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-19T17:35:27.290Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear self-excited thermoacoustic oscillations of a ducted premixed flame: bifurcations and routes to chaos

Published online by Cambridge University Press:  25 November 2014

Karthik Kashinath ,
Iain C. Waugh  and
Matthew P. Juniper
Karthik Kashinath*
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
Iain C. Waugh
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
Matthew P. Juniper
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
*
†Present address: Climate Science Department, Earth Sciences Division, Lawrence Berkeley National Lab, 1 Cyclotron Road, MS74R316C, Berkeley, CA 94720, USA. Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

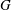Thermoacoustic systems can oscillate self-excitedly, and often non-periodically, owing to coupling between unsteady heat release and acoustic waves. We study a slot-stabilized two-dimensional premixed flame in a duct via numerical simulations of a $G$-equation flame coupled with duct acoustics. We examine the bifurcations and routes to chaos for three control parameters: (i) the flame position in the duct, (ii) the length of the duct and (iii) the mean flow velocity. We observe period-1, period-2, quasi-periodic and chaotic oscillations. For certain parameter ranges, more than one stable state exists, so mode switching is possible. At intermediate times, the system is attracted to and repelled from unstable states, which are also identified. Two routes to chaos are established for this system: the period-doubling route and the Ruelle–Takens–Newhouse route. These are corroborated by analyses of the power spectra of the acoustic velocity. Instantaneous flame images reveal that the wrinkles on the flame surface and pinch-off of flame pockets are regular for periodic oscillations, while they are irregular and have multiple time and length scales for quasi-periodic and aperiodic oscillations. This study complements recent experiments by providing a reduced-order model of a system with approximately 5000 degrees of freedom that captures much of the elaborate nonlinear behaviour of ducted premixed flames observed in the laboratory.

JFM classification

Instability: Instability Nonlinear Dynamical Systems: Nonlinear Dynamical Systems Reacting Flows: Reacting Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 761 , 25 December 2014 , pp. 399 - 430
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Argyris, J., Faust, G. & Haase, M. 1993 Routes to chaos and turbulence: a computational introduction. Phil. Trans. R. Soc. Lond. A 344 (1671), 207–234.Google Scholar
Ashwin, P. & Timme, M. 2005 Unstable attractors: existence and robustness in networks of oscillators with delayed pulse coupling. Nonlinearity 18 (5), 2035–2060.Google Scholar
Baillot, F., Durox, D. & Prud’homme, R. 1992 Experimental and theoretical study of a premixed flame. Combust. Flame 88 (2), 149–168.Google Scholar
Balachandran, R., Dowling, A. P. & Mastorakos, E. 2008 Non-linear response of turbulent premixed flames to imposed inlet velocity oscillations of two frequencies. Flow Turbul. Combust. 80 (4), 455–487.Google Scholar
Balasubramanian, K. & Sujith, R. I. 2008 Non-normality and nonlinearity in combustion–acoustic interaction in diffusion flames. J. Fluid Mech. 594, 29–57.Google Scholar
Bergé, P., Pomeau, Y., Vidal, C. & Tuckerman, L. 1986 Order Within Chaos: Towards a Deterministic Approach to Turbulence. Wiley.Google Scholar
Birbaud, A., Durox, D. & Candel, S. 2006 Upstream flow dynamics of a laminar premixed conical flame submitted to acoustic modulations. Combust. Flame 146 (3), 541–552.Google Scholar
Boudy, F., Durox, D., Schuller, T. & Candel, S. 2013 Analysis of limit cycles sustained by two modes in the flame describing function framework. C. R. Méc. 341 (1), 181–190.Google Scholar
Boyer, L. & Quinard, J. 1990 On the dynamics of anchored flames. Combust. Flame 82 (1), 51–65.CrossRefGoogle Scholar
Culick, F. E. C. 1971 Non-linear growth and limiting amplitude of acoustic oscillations in combustion chambers. Combust. Sci. Technol. 3 (1), 1–16.Google Scholar
Dowling, A. P. 1997 Nonlinear self-excited oscillations of a ducted flame. J. Fluid Mech. 346 (1), 271–290.CrossRefGoogle Scholar
Dowling, A. P. 1999 A kinematic model of a ducted flame. J. Fluid Mech. 394 (1), 51–72.Google Scholar
Ducruix, S., Durox, D. & Candel, S. 2000 Theoretical and experimental determination of the flame transfer function of a laminar premixed flame. Proc. Combust. Inst. 28 (1), 765–773.Google Scholar
Durox, D, Schuller, T & Candel, S 2005 Combustion dynamics of inverted conical flames. Proc. Combust. Inst. 30 (2), 1717–1724.Google Scholar
Eckhardt, B., Schneider, T. M., Hof, B. & Westerweel, J. 2007 Turbulence transition in pipe flow. Annu. Rev. Fluid Mech. 39, 447–468.CrossRefGoogle Scholar
Eckmann, J. P. 1981 Roads to turbulence in dissipative dynamical systems. Rev. Mod. Phys. 53 (4), 643–654.CrossRefGoogle Scholar
Fenstermacher, P. R., Swinney, H. L. & Gollub, J. P. 1979 Dynamical instabilities and the transition to chaotic Taylor vortex flow. J. Fluid Mech. 94 (1), 103–128.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanović, P. 2009 Equilibrium and travelling-wave solutions of plane Couette flow. J. Fluid Mech. 638 (1), 243–266.Google Scholar
Gollub, J. P. & Benson, S. V. 1980 Many routes to turbulent convection. J. Fluid Mech. 100 (3), 449–470.Google Scholar
Gollub, J. P & Swinney, H. L. 1975 Onset of turbulence in a rotating fluid. Phys. Rev. Lett. 35 (14), 927–930.Google Scholar
Gotoda, H., Amano, M., Miyano, T., Ikawa, T., Maki, K. & Tachibana, S. 2012 Characterization of complexities in combustion instability in a lean premixed gas-turbine model combustor. Chaos 22 (4), 043128.Google Scholar
Gotoda, H., Nikimoto, H., Miyano, T. & Tachibana, S. 2011 Dynamic properties of combustion instability in a lean premixed gas-turbine combustor. Chaos 21 (1), 013124.Google Scholar
Gotoda, H., Shinoda, Y., Kobayashi, M., Okuno, Y. & Tachibana, S. 2014 Detection and control of combustion instability based on the concept of dynamical system theory. Phys. Rev. E 89 (2), 022910.Google ScholarPubMed
Gottlieb, S. & Shu, C. 1998 Total variation diminishing Runge–Kutta schemes. Maths Comput. 67 (221), 73–86.Google Scholar
Graham, O. & Dowling, A. P.2011 Low-order modelling of ducted flames with temporally varying equivalence ratio in realistic geometries. ASME Turbo Expo paper, GT 2011-45255.Google Scholar
Grassberger, P. & Procaccia, I. 1983 Characterization of strange attractors. Phys. Rev. Lett. 50 (5), 346–349.Google Scholar
Guzman, A. M. & Amon, C. H. 1994 Transition to chaos in converging–diverging channel flows: Ruelle–Takens–Newhouse scenario. Phys. Fluids 6, 1994, doi:10.1063/1.868206.Google Scholar
Guzman, A. M. & Amon, C. H. 1996 Dynamical flow characterization of transitional and chaotic regimes in converging–diverging channels. J. Fluid Mech. 321 (1), 25–57.Google Scholar
Hegger, R., Kantz, H. & Schreiber, T. 1999 Practical implementation of nonlinear time series methods: the TISEAN package. Chaos 9 (2), 413–435.Google Scholar
Hemchandra, S.2009 Dyamics of turbulent premixed flames in acoustic fields. PhD thesis, Georgia Institute of Technology.Google Scholar
Hemchandra, S. 2012 Premixed flame response to equivalence ratio perturbations: comparison between reduced order modelling and detailed computations. Combust. Flame 159, 3530–3543.Google Scholar
Hemchandra, S. & Lieuwen, T. 2010 Local consumption speed of turbulent premixed flames – an analysis of ‘memory effects’. Combust. Flame 157 (5), 955–965.Google Scholar
Jahnke, C. C. & Culick, F. E. C. 1994 Application of dynamical systems theory to nonlinear combustion instabilities. J. Propul. Power 10 (4), 508–517.Google Scholar
Jiang, G. S. & Peng, D. 2000 Weighted ENO schemes for Hamilton–Jacobi equations. SIAM J. Sci. Comput. 21 (6), 2126–2143.Google Scholar
Juniper, M. P. 2011 Triggering in the horizontal Rijke tube: non-normality, transient growth and bypass transition. J. Fluid Mech. 667, 272–308.CrossRefGoogle Scholar
Kabiraj, L., Saurabh, A., Wahi, P. & Sujith, R. I. 2012 Route to chaos for combustion instability in ducted laminar premixed flames. Chaos 22 (2), 023129.CrossRefGoogle ScholarPubMed
Kabiraj, L. & Sujith, R. I. 2012a Bifurcations of self-excited ducted laminar premixed flames. J. Engng Gas Turbines Power 134, 031502.CrossRefGoogle Scholar
Kabiraj, L. & Sujith, R. I. 2012b Nonlinear self-excited thermoacoustic oscillations: intermittency and flame blowout. J. Fluid Mech. 713, 376–397.CrossRefGoogle Scholar
Kantz, H. 1994 A robust method to estimate the maximal Lyapunov exponent of a time series. Phys. Lett. A 185 (1), 77–87.CrossRefGoogle Scholar
Kantz, H. & Schreiber, T. 2000 Nonlinear Time Series Analysis. Cambridge University Press.Google Scholar
Karimi, N., Brear, M. J., Jin, S.-H. & Monty, J. P. 2009 Linear and non-linear forced response of a conical, ducted, laminar premixed flame. Combust. Flame 156 (11), 2201–2212.Google Scholar
Kashinath, K., Hemchandra, S. & Juniper, M. P. 2013a Nonlinear phenomena in thermoacoustic systems with premixed flames. J. Engng Gas Turbines Power 135, 061502.Google Scholar
Kashinath, K., Hemchandra, S. & Juniper, M. P. 2013b Nonlinear thermoacoustics of ducted premixed flames: the influence of perturbation convection speed. Combust. Flame 160 (12), 2856–2865, doi:10.1016/j.combustflame.2013.06.019.Google Scholar
Kornilov, V. N., Schreel, K. R. A. M. & de Goey, L. P. H. 2007 Experimental assessment of the acoustic response of laminar premixed bunsen flames. Proc. Combust. Inst. 31 (1), 1239–1246.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1959 Fluid Mechanics. Pergamon.Google Scholar
Lei, S. & Turan, A. 2009 Nonlinear/chaotic behaviour in thermo-acoustic instability. Combust. Theor. Model. 13 (3), 541–557.Google Scholar
Li, L. K. B. & Juniper, M. P. 2013 Lock-in and quasiperiodicity in a forced hydrodynamically self-excited jet. J. Fluid Mech. 726, 624–655.Google Scholar
Libchaber, A 1987 From chaos to turbulence in Benard convection. Proc. R. Soc. Lond. A 413 (1844), 63–69.Google Scholar
Lieuwen, T. C. 2005 Nonlinear kinematic response of premixed flames to harmonic velocity disturbances. Proc. Combust. Inst. 30 (2), 1725–1732.Google Scholar
Lieuwen, T. C. 2012 Unsteady Combustor Physics. Cambridge University Press.Google Scholar
Longtin, A. 2003 Effects of noise on nonlinear dynamics. In Nonlinear Dynamics in Physiology and Medicine, Interdisciplinary Applied Mathematics, vol. 25. Springer.Google Scholar
Margolis, S. B. 1993 Nonlinear stability of combustion-driven acoustic oscillations in resonance tubes. J. Fluid Mech. 253, 67–103.Google Scholar
Matveev, I.2003 Thermo-acoustic instabilities in the Rijke tube: experiments and modeling. PhD thesis, California Institute of Technology.Google Scholar
McLaughlin, J. B. & Orszag, S. 1982 Transition from periodic to chaotic thermal convection. J. Fluid Mech. 122, 123–142.CrossRefGoogle Scholar
Milnor, J. 1985 On the concept of attractor. Commun. Math. Phys. 99, 177–195.Google Scholar
Moeck, J. P. & Paschereit, C. O. 2012 Nonlinear interactions of multiple linearly unstable thermoacoustic modes. Intl. J. Spray Combust. Dyn. 4 (1), 1–28.Google Scholar
Nair, V. & Sujith, R. I. 2013 Identifying homoclinic orbits in the dynamics of intermittent signals through recurrence quantification. Chaos 23 (3), 033136.CrossRefGoogle ScholarPubMed
Nair, V., Thampi, G., Karuppusamy, S., Gopalan, S. & Sujith, R. I. 2013 Loss of chaos in combustion noise as a precursor of impending combustion instability. Intl. J. Spray Combust. Dyn. 5 (4), 273–290.Google Scholar
Newhouse, S., Ruelle, D. & Takens, F. 1978 Occurrence of strange axiom $A$ attractors near quasi periodic flows on $T^{m}$ , $m\geqslant 3$ . Commun. Math. Phys. 64 (1), 35–40.Google Scholar
Noiray, N., Durox, D., Schuller, T. & Candel, S. 2008 A unified framework for nonlinear combustion instability analysis based on the flame describing function. J. Fluid Mech. 615, 139–167.Google Scholar
Oberlack, M. & Cheviakov, A. F. 2010 Higher-order symmetries and conservation laws of the $G$ -equation for premixed combustion and resulting numerical schemes. J. Engng Maths 66 (1–3), 121–140.Google Scholar
O’Connor, J. & Lieuwen, T. 2012 Recirculation zone dynamics of a transversely excited swirl flow and flame. Phys. Fluids 24 (7), 075107.Google Scholar
Ott, E. 2002 Chaos in Dynamical Systems. Cambridge University Press.Google Scholar
Peng, D. 1999 A PDE-based fast local level set method. J. Comput. Phys. 155 (2), 410–438.Google Scholar
Poinsot, T. & Candel, S. M. 1988 A nonlinear model for ducted flame combustion instabilities. Combust. Sci. Technol. 61 (4–6), 121–153.Google Scholar
Preetham, H. S. & Lieuwen, T. C. 2008 Dynamics of laminar premixed flames forced by harmonic velocity disturbances. J. Propul. Power 394 (6), 51–72.Google Scholar
Preetham, H. S. & Lieuwen, T. 2004 Nonlinear flame-flow transfer function calculations: flow disturbance celerity effects. In Proceedings of the 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, AIAA Paper 2004–4035.Google Scholar
Ruelle, D. & Takens, F. 1971 On the nature of turbulence. Commun. Math. Phys. 20 (3), 167–192.Google Scholar
Shanbhogue, S. J., Shin, D.-H., Hemchandra, S., Plaks, D. & Lieuwen, T. 2009 Flame sheet dynamics of bluff-body stabilized flames during longitudinal acoustic forcing. Proc. Combust. Inst. 32, 1787–1794.CrossRefGoogle Scholar
Shin, D.-H. & Lieuwen, T. 2013 Flame wrinkle destruction processes in harmonically forced, turbulent premixed flames. J. Fluid Mech. 721, 484–513.Google Scholar
Shin, D.-H., Plaks, D. V., Lieuwen, T., Mondragon, U. M., Brown, C. T. & McDonell, V. G. 2011 Dynamics of a longitudinally forced, bluff body stabilized flame. J. Propul. Power 27 (1), 105–116.Google Scholar
Shreekrishna, H. S. & Lieuwen, T. 2010 Premixed flame response to equivalence ratio perturbations. Combust. Theor. Model. 14 (5), 681–714.Google Scholar
Sterling, J. D. 1993 Nonlinear analysis and modelling of combustion instabilities in a laboratory combustor. Combust. Sci. Technol. 89 (1–4), 167–179.Google Scholar
Stow, S. R. & Dowling, A. P. 2009 A time-domain network model for nonlinear thermoacoustic oscillations. J. Engng Gas Turbines Power 131 (3), 031502, doi:10.1115/1.2981178.Google Scholar
Subramanian, P.2011 Dynamical systems approach to the investigation of thermoacoustic instabilities. PhD thesis, Indian Institute of Technology, Madras.Google Scholar
Subramanian, P., Mariappan, S., Sujith, R. I. & Wahi, P. 2010 Bifurcation analysis of thermoacoustic instability in a horizontal Rijke tube. Intl J. Spray Combust. Dyn. 2 (4), 325–355.Google Scholar
Subramanian, P. & Sujith, R. I. 2011 Non-normality and internal flame dynamics in premixed flame–acoustic interaction. J. Fluid Mech. 679, 315–342.Google Scholar
Theiler, J. 1990 Estimating fractal dimension. J. Opt. Soc. Am. A 7 (6), 1055–1073.Google Scholar
Thompson, J. M. T. & Stewart, H. B. 2002 Nonlinear Dynamics and Chaos. Wiley.Google Scholar
Waugh, I. C.2013 Methods for analysis of nonlinear thermoacoustic systems. PhD thesis, University of Cambridge.Google Scholar
Waugh, I. C. & Juniper, M. P. 2011 Triggering in a thermoacoustic system with stochastic noise. Intl J. Spray Combust. Dyn. 3 (4), 225–242.CrossRefGoogle Scholar
Williams, F. A. 1985 Turbulent Combustion in the Mathematics of Combustion (ed. Buckmaster, J. D.), pp. 97–131. SIAM.Google Scholar