Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T14:42:01.807Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear phase-resolved reconstruction of irregular water waves

Published online by Cambridge University Press:  25 January 2018

Yusheng Qi ,
Guangyu Wu ,
Yuming Liu Open the ORCID record for Yuming Liu [Opens in a new window] ,
Moo-Hyun Kim  and
Dick K. P. Yue Open the ORCID record for Dick K. P. Yue [Opens in a new window]
Yusheng Qi
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Guangyu Wu
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Yuming Liu
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Moo-Hyun Kim
Affiliation:
Department of Civil Engineering, Texas A&M University, College Station, TX 77843, USA
Dick K. P. Yue*
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

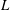We develop and validate a high-order reconstruction (HOR) method for the phase-resolved reconstruction of a nonlinear wave field given a set of wave measurements. HOR optimizes the amplitude and phase of $L$ free wave components of the wave field, accounting for nonlinear wave interactions up to order 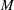$M$ in the evolution, to obtain a wave field that minimizes the reconstruction error between the reconstructed wave field and the given measurements. For a given reconstruction tolerance, 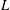$L$ and $M$ are provided in the HOR scheme itself. To demonstrate the validity and efficacy of HOR, we perform extensive tests of general two- and three-dimensional wave fields specified by theoretical Stokes waves, nonlinear simulations and physical wave fields in tank experiments which we conduct. The necessary 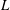$L$, for general broad-banded wave fields, is shown to be substantially less than the free and locked modes needed for the nonlinear evolution. We find that, even for relatively small wave steepness, the inclusion of high-order effects in HOR is important for prediction of wave kinematics not in the measurements. For all the cases we consider, HOR converges to the underlying wave field within a nonlinear spatial-temporal predictable zone 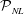${\mathcal{P}}_{NL}$ which depends on the measurements and wave nonlinearity. For infinitesimal waves, 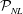${\mathcal{P}}_{NL}$ matches the linear predictable zone 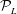${\mathcal{P}}_{L}$, verifying the analytic solution presented in Qi et al. (Wave Motion, vol. 77, 2018, pp. 195–213). With increasing wave nonlinearity, we find that 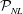${\mathcal{P}}_{NL}$ contains and is generally greater than ${\mathcal{P}}_{L}$. 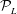Thus ${\mathcal{P}}_{L}$ provides a (conservative) estimate of 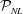${\mathcal{P}}_{NL}$ when the underlying wave field is not known.

JFM classification

Waves/Free-surface Flows: Surface gravity waves Waves/Free-surface Flows: Waves/Free-surface Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 838 , 10 March 2018 , pp. 544 - 572
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Chevron Energy Technology Company, 1400 Smith Street, Houston, TX 77002, USA.

References

Agrawal, Y. C. & Aubrey, D. G. 1992 Velocity observations above a rippled bed using laser Doppler velocimetry. J. Geophys. Res. 97 (C12), 20249–20259.CrossRefGoogle Scholar
Alam, M., Liu, Y. & Yue, D. K. P. 2009 Bragg resonance of waves in a two-layer fluid propagating over bottom ripples. Part 2. Numerical simulation. J. Fluid Mech. 624, 225–253.Google Scholar
Backus, G. & Gilbert, F. 1968 The resolving power of gross earth data. Geophys. J. R. Astron. Soc. 16, 169–205.Google Scholar
Broyden, C. G. 1965 A class of methods for solving nonlinear simultaneous equations. Math. Comput. 19, 577–593.CrossRefGoogle Scholar
Dommermuth, D. G. & Yue, D. K. P. 1987 A high-order spectral method for the study of nonlinear gravity waves. J. Fluid Mech. 184, 267–288.Google Scholar
Fedele, F., Brennan, J., De León, S. P., Dudley, J. & Dias, F. 2016 Real world ocean rogue waves explained without the modulational instability. Sci. Rep. 6, 27715.Google Scholar
Gill, P. E., Murray, W. & Wright, M. H. 1981 Practical Optimization. Academic Press.Google Scholar
Hogan, S. J., Gruman, I. & Stiassnie, M. 1988 On the changes in phase speed of one train of water waves in the presence of another. J. Fluid Mech. 192, 97–114.Google Scholar
Liagre, P F. B.1999 Generation and analysis of multi-directional waves. Master thesis, Texas A&M University.Google Scholar
Liu, Y. & Yue, D. K. P. 1998 On generalized Bragg scattering of surface wave by bottom ripples. J. Fluid Mech. 356, 297–326.CrossRefGoogle Scholar
Longuet-Higgins, M. S. 1962 Resonant interactions between two trains of gravity waves. J. Fluid Mech. 12, 321–332.CrossRefGoogle Scholar
Microway 2017 High performance computing with Intel Xeon HPC clusters. https://www.microway.com/products/hpc-clusters/high-performance-computing-with-intel-xeon-hpc-clusters.Google Scholar
Mosegaard, K. 1998 Resolution analysis of general inverse problems through inverse Monte Carlo sampling. Inverse Problems 14 (3), 405–426.Google Scholar
Nieto-Borge, J. C., Rodrguez, G., Hessner, K. & Izquierdo, P. 2004 Inversion of marine radar images for surface wave analysis. J. Atmos. Ocean. Technol. 21 (8), 1291–1300.Google Scholar
Qi, Y., Wu, G., Liu, Y. & Yue, D. K. P. 2018 Predictable zone for phase-resolved reconstruction and forecast of irregular waves. Wave Motion 77, 195–213.Google Scholar
Qi, Y., Xiao, W. & Yue, D. K. P. 2016 Phase-resolved wave field simulation calibration of sea surface reconstruction using noncoherent marine radar. J. Atmos. Ocean. Technol. 33 (6), 1135–1149.Google Scholar
Rainey, R. C. T. 1995 Slendy-body expressions for the wave load on offshore structures. Proc. R. Soc. Lond. A 450, 391–416.Google Scholar
Schwartz, L. W. 1974 Computer extension and analytic continuation of Stokes’ expansion for gravity waves. J. Fluid Mech. 62, 553–578.Google Scholar
Simanesew, A., Trulsen, K., Krogstad, H. E. & Nieto-Borge, J. C. 2017 Surface wave predictions in weakly nonlinear directional seas. Appl. Ocean Res. 65, 79–89.CrossRefGoogle Scholar
Skjelbreia, J. E.1987 Observations of breaking waves on sloping bottoms by use of laser doppler velocimetry. PhD thesis, California Institute of Technology.Google Scholar
Snieder, R. 1991 An extension of Backus–Gilbert theory to nonlinear inverse problems. Inverse Problems 7 (3), 409–433.Google Scholar
Snieder, R. 1998 The role of nonlinearity in inverse problems. Inverse Problems 14, 387–404.Google Scholar
Stansberg, C. T. 1993 Second-order numerical reconstruction of laboratory generated random waves. In Proceedings of the 10th International Offshore Mechanics and Arctic Engineering Conference, vol. 1, pp. 143–157. ASME.Google Scholar
Wu, G.2004 Direct simulation and deterministic prediction of large-scale nonlinear ocean wave-field. PhD thesis, Massachusetts Institute of Technology.Google Scholar
Young, I. R. 1994 On the measurement of directional wave spectra. Appl. Ocean Res. 16, 1283–1294.Google Scholar
Zhang, J., Chen, L., Ye, M. & Randall, R. E. 1996 Hybrid wave model for unidirectional irregular waves. Part 1. Theory and numerical scheme. Appl. Ocean Res. 18 (2–3), 77–92.Google Scholar
Zhang, J., Yang, J., Wen, J., Prislin, I. & Hong, K. 1999 Deterministic wave model for short-crested ocean waves. Part 1. Theory and numerical scheme. Appl. Ocean Res. 21 (4), 167–188.CrossRefGoogle Scholar