Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T16:55:30.702Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear limiting dynamics of a shrinking interface in a Hele-Shaw cell

Published online by Cambridge University Press:  18 January 2021

Meng Zhao Open the ORCID record for Meng Zhao [Opens in a new window] ,
Zahra Niroobakhsh ,
John Lowengrub Open the ORCID record for John Lowengrub [Opens in a new window]  and
Shuwang Li
Meng Zhao
Affiliation:
Department of Mathematics, University of California at Irvine, Irvine, CA92617, USA
Zahra Niroobakhsh
Affiliation:
Department of Civil and Mechanical Engineering, University of Missouri-Kansas City, Kansas City, MO64110, USA
John Lowengrub*
Affiliation:
Department of Mathematics, University of California at Irvine, Irvine, CA92617, USA Department of Biomedical Engineering, Center for Complex Biological Systems University of California at Irvine, Irvine, CA92617, USA
Shuwang Li*
Affiliation:
Department of Applied Mathematics, Illinois Institute of Technology, Chicago, IL60616, USA
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

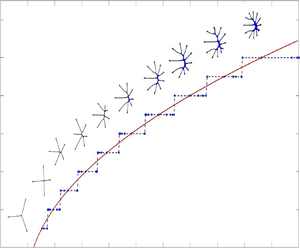
The flow in a Hele-Shaw cell with a time-increasing gap poses a unique shrinking interface problem. When the upper plate of the cell is lifted perpendicularly at a prescribed speed, the exterior less viscous fluid penetrates the interior more viscous fluid, which generates complex, time-dependent interfacial patterns through the Saffman–Taylor instability. The pattern formation process sensitively depends on the lifting speed and is still not fully understood. For some lifting speeds, such as linear or exponential speed, the instability is transient and the interface eventually shrinks as a circle. However, linear stability analysis suggests there exist shape invariant shrinking patterns if the gap $b(t)$ is increased more rapidly: $b(t)=\left (1-({7}/{2})\tau \mathcal {C} t\right )^{-{2}/{7}}$, where $\tau$ is the surface tension and $\mathcal {C}$ is a function of the interface perturbation mode $k$. Here, we use a spectrally accurate boundary integral method together with an efficient time adaptive rescaling scheme, which for the first time makes it possible to explore the nonlinear limiting dynamical behaviour of a vanishing interface. When the gap is increased at a constant rate, our numerical results quantitatively agree with experimental observations (Nase et al., Phys. Fluids, vol. 23, 2011, 123101). When we use the shape invariant gap $b(t)$, our nonlinear results reveal the existence of $k$-fold dominant, one-dimensional, web-like networks, where the fractal dimension is reduced to almost unity at late times. We conclude by constructing a morphology diagram for pattern selection that relates the dominant mode $k$ of the vanishing interface and the control parameter $\mathcal {C}$.

JFM classification

Interfacial Flows (free surface): Fingering instability Nonlinear Dynamical Systems: Pattern formation Low-Reynolds-number flows: Boundary integral methods
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 910 , 10 March 2021 , A41
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Anjos, P.H.A., Dias, E.O. & Miranda, J.A. 2017 Inertia-induced dendriticlike patterns in lifting Hele-Shaw flows. Phys. Rev. Fluids 2, 014003.CrossRefGoogle Scholar
Anjos, P.H.A. & Miranda, J.A. 2014 Influence of wetting on fingering patterns in lifting Hele-Shaw flows. Soft Matt. 10, 7459–7467.CrossRefGoogle ScholarPubMed
Ben Amar, M. & Bonn, D. 2005 Fingering instabilities in adhesive failure. Physica D 209 (1–4), 1–16.CrossRefGoogle Scholar
Ben-Jacob, E., Deutscher, G., Garik, P., Goldenfeld, N.D. & Lareah, Y. 1986 Formation of a dense branching morphology in interfacial growth. Phys. Rev. Lett. 57, 1903–1906.CrossRefGoogle ScholarPubMed
Ben-Jacob, E. & Garik, P. 1990 The formation of patterns in non-equilibrium growth. Nature 343, 523–530.CrossRefGoogle Scholar
Chen, C.-Y., Chen, C.-H. & Miranda, J.A. 2005 Numerical study of miscible fingering in a time-dependent gap Hele-Shaw cell. Phys. Rev. E 71, 056304.CrossRefGoogle Scholar
Chen, C.-Y., Huang, C.W., Wang, L.C. & Miranda, J.A. 2010 Controlling radial fingering patterns in miscible confined flows. Phys. Rev. E 82, 056308.CrossRefGoogle ScholarPubMed
Chevalier, C., Ben Amar, M., Bonn, D. & Lindner, A. 2006 Inertial effects on Saffman–Taylor viscous fingering. J. Fluid Mech. 552, 83–97.CrossRefGoogle Scholar
Chuoke, R., van Meurs, P. & van der Poel, C. 1959 The instability of slow immiscible viscous liquid–liquid displacements in permeable media. Trans. AIME 216, 188–194.CrossRefGoogle Scholar
Cummins, H.Z., Fourtune, L. & Rabaud, M. 1993 Successive bifurcations in directional viscous fingering. Phys. Rev. E 47, 1727–1738.CrossRefGoogle ScholarPubMed
Dallaston, M.C. & McCue, S.W. 2013 Bubble extinction in Hele-Shaw flow with surface tension and kinetic undercooling regularization. Nonlinearity 26, 1639–1665.CrossRefGoogle Scholar
Dallaston, M.C. & McCue, S.W. 2016 A curve shortening flow rule for closed embedded plane curves with a prescribed rate of change in enclosed area. Proc. R. Soc. Lond. A 472, 20150629.Google ScholarPubMed
Derks, D., Lindner, A., Creton, C. & Bonn, D. 2003 Cohesive failure of thin layers of soft model adhesives under tension. J. Appl. Phys. 93, 1557–1566.CrossRefGoogle Scholar
Dias, E.O. & Miranda, J.A. 2010 Control of radial fingering patterns: a weakly nonlinear approach. Phys. Rev. E 81, 016312.CrossRefGoogle ScholarPubMed
Dias, E.O. & Miranda, J.A. 2013 a Determining the number of fingers in the lifting Hele-Shaw problem. Phys. Rev. E 88, 043002.CrossRefGoogle ScholarPubMed
Dias, E.O. & Miranda, J.A. 2013 b Taper-induced control of viscous fingering in variable-gap Hele-Shaw flows. Phys. Rev. E 87, 053015.CrossRefGoogle ScholarPubMed
Francis, B. & Horn, R. 2001 Apparatus-specific analysis of fluid adhesion measurements. J. Appl. Phys. 89, 4167–4174.CrossRefGoogle Scholar
He, A. & Belmonte, A. 2011 Inertial effects on viscous fingering in the complex plane. J. Fluid Mech. 668, 436–445.CrossRefGoogle Scholar
Jackson, S.J., Stevens, D., Giddings, D. & Power, H. 2015 Dynamic-wetting effects in finite-mobility-ratio Hele-Shaw flow. Phys. Rev. E 92, 023021.CrossRefGoogle ScholarPubMed
Kaufman, J.H., Melroy, O.R. & Dimino, G.M. 1989 Information-theoretic study of pattern formation: rate of entropy production of random fractals. Phys. Rev. A 39, 1420–1428.CrossRefGoogle ScholarPubMed
Lakrout, H., Sergot, P. & Creton, C. 1999 Direct observation of cavitation and fibrillation in a probe tack experiment on model acrylic pressure-sensitive-adhesives. J. Adhes. 69, 307–359.CrossRefGoogle Scholar
Lamb, H. 1932 Hydrodynamics. Cambridge University Press.Google Scholar
Langer, J. 1980 Instabilities and pattern formation in crystal growth. Rev. Mod. Phys. 52, 1–28.CrossRefGoogle Scholar
Langer, J. 1989 Dendrites, viscous fingers, and the theory of pattern formation. Science 243 (4895), 1150–1156.CrossRefGoogle ScholarPubMed
Li, S., Lowengrub, J.S., Fontana, J. & Palffy-Muhoray, P. 2009 Control of viscous fingering patterns in a radial Hele-Shaw cell. Phys. Rev. Lett. 102, 174501.CrossRefGoogle Scholar
Li, S., Lowengrub, J.S. & Leo, P.H. 2007 A rescaling scheme with application to the long-time simulation of viscous fingering in a Hele-Shaw cell. J. Comput. Phys. 225 (1), 554–567.CrossRefGoogle Scholar
Lindner, A., Derks, D. & Shelley, M.J. 2005 Stretch flow of thin layers of Newtonian liquids: fingering patterns and lifting forces. Phys. Fluids 17, 072107.CrossRefGoogle Scholar
McKinley, G.H. & Sridhar, T. 2002 Filament-stretching rheometry of complex fluids. Annu. Rev. Fluid Mech. 34, 375–415.CrossRefGoogle Scholar
McLean, J. & Saffman, P. 1981 The effect of surface tension on the shape of fingers in a Hele-Shaw cell. J. Fluid Mech. 102, 455–469.CrossRefGoogle Scholar
Mullins, W.W. & Sekerka, R.F. 1963 Morphological stability of a particle growing by diffusion or heat flow. J. Appl. Phys. 34 (2), 323–329.CrossRefGoogle Scholar
Nase, J., Derks, D. & Lindner, A. 2011 Dynamic evolution of fingering patterns in a lifted Hele-Shaw cell. Phys. Fluids 23, 123101.CrossRefGoogle Scholar
Park, C.W., Gorell, S. & Homsy, G.M. 1984 Two-phase displacement in Hele-Shaw cells: experiments on viscously driven instabilities. J. Fluid Mech. 141, 257–287.CrossRefGoogle Scholar
Park, C.W. & Homsy, G.M. 1984 Two-phase displacement in Hele-Shaw cells: theory. J. Fluid Mech. 139, 291–308.CrossRefGoogle Scholar
Poivet, S., Nallet, F., Gay, C. & Fabre, P. 2003 Cavitation-induced force transition in confined viscous liquids under traction. EPL 62, 244–250.CrossRefGoogle Scholar
Praud, O. & Swinney, H. 2005 Fractal dimension and unscreened angles measured for radial viscous fingering. Phys. Rev. E 72 (1), 011406.CrossRefGoogle ScholarPubMed
Saad, Y. & Schultz, M.H. 1986 GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 7, 856–869.CrossRefGoogle Scholar
Saffman, P.G. & Taylor, G. 1958 The penetration of a fluid into a porous medium or a Hele-Shaw cell containing a more viscous fluid. Proc. R. Soc. Lond. A 245 (1242), 312–329.Google Scholar
Shelley, M.J., Tian, F.R. & Wlodarski, K. 1997 Hele-Shaw flow and pattern formation in a time-dependent gap. Nonlinearity 10, 1471–1495.CrossRefGoogle Scholar
Sinha, S., Dutta, T. & Tarafdar, S. 2008 Adhesion and fingering in the lifting Hele-Shaw cell: role of the substrate. Eur. Phys. J. E 25, 267–275.CrossRefGoogle ScholarPubMed
Sinha, S. & Tarafdar, S. 2009 Viscous fingering patterns and evolution of their fractal dimension. Ind. Engng Chem. Res. 48, 8837–8841.CrossRefGoogle Scholar
Tatulchenkov, A. & Cebers, A. 2008 Magnetic fluid labyrinthine instability in Hele-Shaw cell with time dependent gap. Phys. Fluids 20, 054101.CrossRefGoogle Scholar
Zhang, S.-Z., Louis, E., Pla, O. & Guinea, F. 1998 Linear stability analysis of the Hele-Shaw cell with lifting plates. Eur. Phys. J. B 1 (1), 123–127.CrossRefGoogle Scholar
Zhao, M., Belmonte, A., Li, S., Li, X. & Lowengrub, J. 2016 Nonlinear simulations of elastic fingering in a Hele-Shaw cell. J. Comput. Appl. Maths 307, 394–407.CrossRefGoogle Scholar
Zhao, M., Li, X., Yin, W., Belmonte, A., Lowengrub, J.S. & Li, S. 2018 Computation of a shrinking interface in a Hele-Shaw cell. SIAM J. Sci. Comput. 40, B1206–B1228.CrossRefGoogle Scholar
Zhao, M., Yin, W., Lowengrub, J. & Li, S. 2017 An efficient adaptive rescaling scheme for computing moving interface problems. Commun. Comput. Phys. 21, 679–691.CrossRefGoogle Scholar
Zosel, A. 1985 Adhesion and tack of polymers: influence of mechanical properties and surface tensions. Colloid Polym. Sci. 263, 541–553.CrossRefGoogle Scholar