Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T15:28:26.515Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear electrophoresis of a tightly fitting sphere in a cylindrical tube

Published online by Cambridge University Press:  28 March 2018

J. D. Sherwood Open the ORCID record for J. D. Sherwood [Opens in a new window]  and
S. Ghosal
J. D. Sherwood*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, CambridgeCB3 0WA, UK
S. Ghosal
Affiliation:
Department of Mechanical Engineering, and Department of Engineering Sciencesand Applied Mathematics, Northwestern University, 2145 Sheridan Rd, Evanston, IL 60208, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate electrophoresis of a tightly fitting sphere of radius 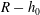$R-h_{0}$ on the axis of a circular tube of radius 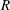$R$, using lubrication theory and ideas due to Schnitzer & Yariv (Phys. Fluids, vol. 26, 2014, 122002). The electrical charge clouds on both the cylindrical wall and the surface of the sphere are assumed thin compared to the gap between the sphere and cylinder, so that charge clouds do not overlap and ion exclusion effects are minimal. Nevertheless, non-uniform pumping of counter-ions within the charge clouds leads to a change in the ionic concentration outside the charge clouds in the narrow gap between sphere and cylinder. The electro-osmotic slip velocities at the two surfaces are modified, leading to a decrease in the electrophoretic velocity of the sphere at low Péclet numbers and an increase in the velocity at high Péclet numbers. When the field strength 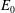$E_{0}$ is low, it is known that the electrophoretic velocity 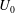$U_{0}$ is proportional to $E_{0}(\unicode[STIX]{x1D701}_{s}-\unicode[STIX]{x1D701}_{c})$ which is zero when the zeta potential 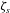$\unicode[STIX]{x1D701}_{s}$ on the sphere surface is equal to the zeta potential 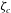$\unicode[STIX]{x1D701}_{c}$ on the cylinder. The perturbation to the above low field strength electrophoretic velocity (at high Péclet number) is predicted to be proportional to 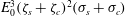$E_{0}^{3}(\unicode[STIX]{x1D701}_{s}+\unicode[STIX]{x1D701}_{c})^{2}(\unicode[STIX]{x1D70E}_{s}+\unicode[STIX]{x1D70E}_{c})$, where 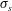$\unicode[STIX]{x1D70E}_{s}$ and 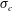$\unicode[STIX]{x1D70E}_{c}$ are the surface charge densities on the sphere and cylinder. The choice of materials with similar or identical zeta potentials (and surface charge densities) for the cylinder and sphere should therefore facilitate the observation of velocities nonlinear in the field strength 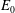$E_{0}$, since the reference linear electrophoretic velocity will be small.

JFM classification

Complex Fluids: Colloids Low-Reynolds-number flows: Lubrication theory Micro-/Nano-fluid dynamics: Micro-/Nano-fluid dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 843 , 25 May 2018 , pp. 847 - 871
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chiu, H. C. & Keh, H. J. 2016 Electrophoresis of a colloidal sphere with double-layer polarization in a microtube. Microfluid Nanofluid 20, 64.Google Scholar
Dukhin, S. S. & Shilov, V. N. 1974 Dielectric Phenomena and the Double Layer in Disperse Systems and Polyelectrolytes. Wiley.10.1149/1.2402374Google Scholar
Fixman, M. 1980 Charged macromolecules in external fields. I. The sphere. J. Chem. Phys. 72, 5177–5186.Google Scholar
Hinch, E. J., Sherwood, J. D., Chew, W. C. & Sen, P. 1984 Dielectric response of a dilute suspension of spheres with thin double layers in an asymmetric electrolyte. J. Chem. Soc. Faraday Trans. 2 80, 535–551.Google Scholar
Hsu, J.-P. & Chen, Z.-S. 2007 Electrophoresis of a sphere along the axis of a cyindrical pore: effects of double-layer polarization and electroosmotic flow. Langmuir 23, 6198–6204.10.1021/la070079mGoogle Scholar
Kang, Y. & Li, D. 2009 Electrophoretic motion of particles and cells in microchannels. Microfluid Nanofluid 6, 431–460.Google Scholar
Keh, H. J. & Anderson, J. L. 1985 Boundary effects on electrophoretic motion of colloidal spheres. J. Fluid Mech. 153, 417–439.10.1017/S002211208500132XGoogle Scholar
Keh, H. J. & Chiou, J. Y. 1996 Electrophoresis of a colloidal sphere in a circular cylindrical pore. AIChE J. 42, 1397–1406.10.1002/aic.690420520Google Scholar
O’Brien, R. W. 1983 The solution of the electrokinetic equations for colloidal particles with thin double layers. J. Colloid Interface Sci. 92, 204–216.10.1016/0021-9797(83)90129-7Google Scholar
Schnitzer, O. & Yariv, E. 2012a Dielectric-solid polarization at strong fields: breakdown of Smoluchowski’s electrophoresis formula. Phys. Fluids 24, 082005.Google Scholar
Schnitzer, O. & Yariv, E. 2012b Macroscale description of electrokinetic flows at large zeta potentials: nonlinear surface conduction. Phys. Rev. E 86, 021503.Google Scholar
Schnitzer, O. & Yariv, E. 2012c Strong-field electrophoresis. J. Fluid Mech. 701, 333–351.Google Scholar
Schnitzer, O. & Yariv, E. 2014 Nonlinear electrophoresis at arbitrary field strengths: small-Dukhin-number analysis. Phys. Fluids 26, 122002.Google Scholar
Schnitzer, O., Zeyde, R., Yavneh, I. & Yariv, E. 2013 Weakly nonlinear electrophoresis of a highly charged colloidal particle. Phys. Fluids 25, 052004.10.1063/1.4804672Google Scholar
Singer, A. & Norbury, J. 2009 A Poisson–Nernst–Planck model for biological ion channels – an asymptotic analysis in a three-dimensional narrow funnel. SIAM J. Appl. Maths 70, 949–968.Google Scholar
Tokarz, M., Hakonen, B., Dommersnes, P., Orwar, O. & Ȧkerman, B. 2007 Electrophoretic transport of latex particles in lipid nanotubes. Langmuir 23, 7652–7658.10.1021/la700336uGoogle Scholar
Xuan, X., Raghibizadeh, S. & Li, D. 2006 Wall effects on electrophoretic motion of spherical polystyrene particles in a rectangular poly(dimethylsiloxane) microchannel. J. Colloid Interface Sci. 296, 743–748.10.1016/j.jcis.2005.09.039Google Scholar
Yariv, E. 2006 ‘Force-free’ electrophoresis? Phys. Fluids 18, 031702.Google Scholar
Yariv, E. 2016a Dielectrophoretic sphere-wall repulsion due to a uniform electric field. Soft Matt. 12, 6277–6284.Google Scholar
Yariv, E. 2016b The electrophoretic mobilities of a circular cylinder in close proximity to a dielectric wall. J. Fluid Mech. 804, R5.10.1017/jfm.2016.579Google Scholar
Yariv, E. & Brenner, H. 2002 The electrophoretic mobility of an eccentrically positioned spherical particle in a cylindrical pore. Phys. Fluids 14, 3354–3357.Google Scholar
Yariv, E. & Brenner, H. 2003 The electrophoretic mobility of a closely fitting sphere in a cylindrical pore. SIAM J. Appl. Maths 64, 423–441.Google Scholar
Ye, C., Xuan, X. & Li, D. 2005 Eccentric electrophoretic motion of a sphere in circular cylindrical microchannels. Microfluid Nanofluid 1, 234–241.Google Scholar