Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T00:51:17.676Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear dynamics induced by linear wave interactions in multilayered flows

Published online by Cambridge University Press:  06 March 2017

Anirban Guha Open the ORCID record for Anirban Guha [Opens in a new window]  and
Firdaus E. Udwadia
Anirban Guha*
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology Kanpur, UP 208016, India
Firdaus E. Udwadia
Affiliation:
Departments of Aerospace and Mechanical Engineering, Civil Engineering, Mathematics, and Information and Operations Management, University of Southern California, 430K Olin Hall, Los Angeles, CA 90089-1453, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Using simple kinematics, we propose a general theory of linear wave interactions between the interfacial waves of a two-dimensional (2D), inviscid, multilayered fluid system. The strength of our formalism is that one does not have to specify the physics of the waves in advance. Wave interactions may lead to instabilities, which may or may not be of the familiar ‘normal-mode’ type. Contrary to intuition, the underlying dynamical system describing linear wave interactions is found to be nonlinear. Specifically, a saw-tooth jet profile with three interfaces possessing kinematic and geometric symmetry is explored. Fixed points of the system for different ranges of a Froude number like control parameter 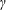$\unicode[STIX]{x1D6FE}$ are derived, and their stability evaluated. Depending upon the initial condition and 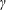$\unicode[STIX]{x1D6FE}$, the dynamical system may reveal transient growth, weakly positive Lyapunov exponents, as well as different nonlinear phenomena such as the formation of periodic and pseudo-periodic orbits. All these occur for those ranges of 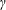$\unicode[STIX]{x1D6FE}$ where normal-mode theory predicts neutral stability. Such rich nonlinear phenomena are not observed in a 2D dynamical system resulting from the two-wave problem, which reveals only stable and unstable nodes.

JFM classification

Instability: Instability Wakes/Jets: Shear layers Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 816 , 10 April 2017 , pp. 412 - 427
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baines, P. G. & Mitsudera, H. 1994 On the mechanism of shear flow instabilities. J. Fluid Mech. 276, 327–342.Google Scholar
Biancofiore, L., Gallaire, F. & Heifetz, E. 2015 Interaction between counterpropagating Rossby waves and capillary waves in planar shear flows. Phys. Fluids 27 (4), 044104.CrossRefGoogle Scholar
Bretherton, F. P. 1966 Baroclinic instability and the short wavelength cut-off in terms of potential vorticity. Q. J. R. Meteorol. Soc. 92 (393), 335–345.CrossRefGoogle Scholar
Carpenter, J. R., Tedford, E. W., Heifetz, E. & Lawrence, G. A. 2013 Instability in stratified shear flow: review of a physical interpretation based on interacting waves. Appl. Mech. Rev. 64 (6), 060801.Google Scholar
Caulfield, C. P. 1994 Multiple linear instability of layered stratified shear flow. J. Fluid Mech. 258, 255–285.Google Scholar
Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability, 2nd edn. Cambridge University Press.Google Scholar
Dritschel, D. G. & McIntyre, M. E. 2008 Multiple jets as PV staircases: the Phillips effect and the resilience of eddy-transport barriers. J. Atmos. Sci. 65 (3), 855–874.Google Scholar
Farrell, B. F. & Ioannou, P. J. 1996 Generalized stability theory. Part I: autonomous operators. J. Atmos. Sci. 53 (14), 2025–2040.Google Scholar
Guha, A. & Lawrence, G. A. 2014 A wave interaction approach to studying non-modal homogeneous and stratified shear instabilities. J. Fluid Mech. 755, 336–364.Google Scholar
Heifetz, E., Bishop, C. H. & Alpert, P. 1999 Counter-propagating Rossby waves in the barotropic Rayleigh model of shear instability. Q. J. R. Meteorol. Soc. 125 (560), 2835–2853.Google Scholar
Heifetz, E., Mak, J., Nycander, J. & Umurhan, O. M. 2015 Interacting vorticity waves as an instability mechanism for magnetohydrodynamic shear instabilities. J. Fluid Mech. 767, 199–225.Google Scholar
Heifetz, E. & Methven, J. 2005 Relating optimal growth to counterpropagating Rossby waves in shear instability. Phys. Fluids 17 (6), 064107.Google Scholar
Moyers-Gonzalez, M. A. & Frigaard, I. A. 2004 Numerical solution of duct flows of multiple visco-plastic fluids. J. Non-Newtonian Fluid Mech. 122 (1), 227–241.CrossRefGoogle Scholar
Rabinovich, A., Umurhan, O. M., Harnik, N., Lott, F. & Heifetz, E. 2011 Vorticity inversion and action-at-a-distance instability in stably stratified shear flow. J. Fluid Mech. 670, 301–325.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Scott, R. K. & Dritschel, D. G. 2012 The structure of zonal jets in geostrophic turbulence. J. Fluid Mech. 711, 576–598.CrossRefGoogle Scholar
Sutherland, B. R. 2010 Internal Gravity Waves. Cambridge University Press.Google Scholar
Taylor, G. I. 1931 Effect of variation in density on the stability of superposed streams of fluid. Proc. R. Soc. Lond. A 132, 499–523.Google Scholar
Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscoll, T. A. 1993 Hydrodynamic stability without eigenvalues. Science 261, 578–584.Google Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-Scale Circulation. Cambridge University Press.Google Scholar
Wolf, A., Swift, J. B., Swinney, H. L. & Vastano, J. A. 1985 Determining Lyapunov exponents from a time series. Physica D 16 (3), 285–317.Google Scholar
Woods, J. D. 1968 Wave-induced shear instability in the summer thermocline. J. Fluid Mech. 32 (4), 791–800.Google Scholar
Yoshida, Z. 2010 Nonlinear Science: The Challenge of Complex Systems. Springer.Google Scholar