Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-28T13:44:31.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear axisymmetric Taylor–Couette flow in a dilute gas: multiroll transition and the role of compressibility

Published online by Cambridge University Press:  08 December 2020

Pratik Aghor  and
Meheboob Alam Open the ORCID record for Meheboob Alam [Opens in a new window]
Pratik Aghor
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur P.O., Bangalore560064, India
Meheboob Alam*
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur P.O., Bangalore560064, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

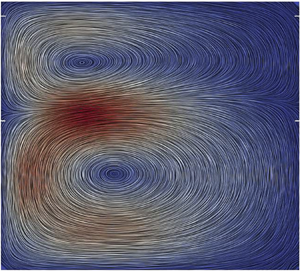
The compressible Navier–Stokes–Fourier equations are numerically solved for axially bounded Taylor–Couette flow (TCF) of an ideal gas, with rotating inner cylinder and stationary outer cylinder, to understand the roles of compressibility and finite aspect ratio on the genesis of nonlinear Taylor vortices and the related bifurcation scenario. Restricting to the axisymmetric case in the wide-gap limit, the aspect ratio $\varGamma =h/\delta$ (where $\delta$ is the annular gap between two cylinders and $h$ is the height of the cylinders) is changed quasistatically by varying the height of the cylinders, following the experimental protocol of Benjamin (Proc. R. Soc. Lond. A, vol. 359, 1978b, pp. 27–43). The symmetric even-numbered ($2,4,6,\ldots$) vortices are found at $\varGamma \geq 2$, whereas the asymmetric 2-roll modes (called the single-roll or ‘anomalous’ modes), that break the midplane $Z_{2}$-symmetry, are uncovered at $\varGamma \leq O(1)$. The phase boundaries of both symmetric and asymmetric rolls and the coexisting regions of different number of rolls are identified in the ($\varGamma , Re$)-plane. These phase diagrams, along with related bifurcation diagrams and various patterns, at finite Mach numbers ($Ma$) are contrasted with their incompressible ($Ma\to 0$) analogues. It is shown that the ‘$1\leftrightarrow 2$’-roll transition in small aspect ratio cylinders is subcritical in compressible TCF in contrast to the supercritical nature of bifurcation in its incompressible counterpart. In general, the gas compressibility has a stabilizing effect on nonlinear Taylor vortices as the underlying phase diagrams in the ($\varGamma , Re$)-plane are shifted to larger values of $Re$ with increasing $Ma$. The stabilizing role of compressibility can be tied to the weakening of the outward jets, which is further aided by the strengthening of the Ekman vortices with increasing Mach number.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Nonlinear Dynamical Systems: Pattern formation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 908 , 10 February 2021 , A24
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ahrens, J., Geveci, B. & Law, C. 2005 Paraview: an end-user tool for large data visualization. In The Visualization Handbook (ed. C. D. Hansen & C. R. Johnson), pp. 717–731. Elsevier.CrossRefGoogle Scholar
Andereck, C. D., Liu, S. S. & Swinney, H. L. 1986 Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164, 155–183.CrossRefGoogle Scholar
Barkley, D. 2016 Theoretical perspectives on the route to turbulence in a pipe. J. Fluid Mech. 803, P1.CrossRefGoogle Scholar
Benjamin, T. B. 1978 a Bifurcation phenomena in steady flows of a viscous fluid. I. Theory. Proc. R. Soc. Lond. A 359, 1–26.Google Scholar
Benjamin, T. B. 1978 b Bifurcation phenomena in steady flows of a viscous fluid. II. Experiments. Proc. R. Soc. Lond. A 359, 27–43.Google Scholar
Benjamin, T. B. & Mullin, T. 1981 Anomalous modes in the Taylor experiment. Proc. R. Soc. Lond. A 377, 221–249.Google Scholar
Benjamin, T. B. & Mullin, T. 1982 Notes on the multiplicity of flows in the Taylor experiment. J. Fluid Mech. 121, 219–230.CrossRefGoogle Scholar
Bolstad, J. H. & Keller, H. B. 1987 Computation of anomalous modes in the Taylor experiment. J. Comput. Phys. 69, 230–251.CrossRefGoogle Scholar
Chandrasekhar, S. 1960 The stability of non-dissipative Couette flow in hydromagnetics. Proc. Natl Acad. Sci. USA 46, 253–257.CrossRefGoogle ScholarPubMed
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Oxford University Press.Google Scholar
Chapman, S. & Cowling, T. G. 1970 The Mathematical Theory of Non-uniform Gases. Cambridge University Press.Google Scholar
Cliffe, K. A. 1983 Numerical calculations of two-cell and single-cell Taylor flows. J. Fluid Mech. 135, 219–230.CrossRefGoogle Scholar
Cliffe, K. A. 1988 Numerical calculations of the primary-flow exchange process in two-cell and single-cell Taylor flows. J. Fluid Mech. 197, 57–79.CrossRefGoogle Scholar
Cliffe, K. A., Mullin, T. & Schaeffer, D. G. 2012 The onset of steady vortices in Taylor–Couette flow: The role of approximate symmetry. Phys. Fluids 24, 064102.CrossRefGoogle Scholar
Cole, J. A. 1976 Taylor-vortex instability and annulus-length effects. J. Fluid Mech. 75, 1–15.CrossRefGoogle Scholar
Coles, D. 1965 Transition in circular Couette flow. J. Fluid Mech. 21, 385–425.CrossRefGoogle Scholar
DiPrima, R. C. & Swinney, H. L. 1981 Instabilities and transition in flow between concentric rotating cylinders. In Hydrodynamic Instabilities and the Transition to Turbulence (ed. J. P. Gollub & H. L. Swinney), pp. 139–180. Springer.CrossRefGoogle Scholar
Furukawa, H., Watanabe, T., Toya, Y. & Nakamura, I. 2002 Flow pattern exchange in the Taylor–Couette system with a very small aspect ratio. Phys. Rev. E 65, 036306.CrossRefGoogle ScholarPubMed
Gollub, J. P. & Swinney, H. L. 1975 Onset of turbulence in a rotating fluid. Phys. Rev. Lett. 35, 927–930.CrossRefGoogle Scholar
Gopan, N. & Alam, M. 2020 Symmetry-breaking bifurcations and hysteresis in compressible Taylor–Couette flow of a dense gas: a molecular dynamics study. J. Fluid Mech. 902, A18.CrossRefGoogle Scholar
Grossmann, S., Lohse, D. & Sun, C. 2016 High-Reynolds number Taylor–Couette turbulence. Annu. Rev. Fluid Mech. 48, 53–80.CrossRefGoogle Scholar
Hall, P. 1982 Centrifugal instabilities of circumferential flows in finite cylinders: the wide gap problem. Proc. R. Soc. Lond. A 384, 359–377.Google Scholar
Harada, I. 1980 Computation of strongly compressible rotating flows. J. Comput. Phys. 38, 335–356.CrossRefGoogle Scholar
Hatay, F. F., Biringen, S., Erlebacher, G. & Zorumski, W. E. 1993 Stability of high-speed compressible rotating Couette flow. Phys. Fluids A 5, 393–404.CrossRefGoogle Scholar
Jones, C. A. 1981 Nonlinear Taylor vortices and their stability. J. Fluid Mech. 102, 253–265.CrossRefGoogle Scholar
Jones, C. A. 1985 The transition to wavy Taylor vortices. J. Fluid Mech. 157, 135–162.CrossRefGoogle Scholar
Kao, K. H. & Chow, C. -Y. 1992 Linear stability of compressible Taylor–Couette flow. Phys. Fluids 4, 994–996.CrossRefGoogle Scholar
Kuhlthau, A. R. 1949 Air friction on rapidly moving surfaces. J. Appl. Phys. 20, 217–223.CrossRefGoogle Scholar
Kuhlthau, A. R. 1960 Recent low-density experiments using rotating cylinder techniques. In Rarefied Gas Dynamics (ed. F. M. Devienne), pp. 192–200. Pergamon.Google Scholar
Liepmann, H. W. & Roshko, A. 1961 Elements of Gas Dynamics. Dover.Google Scholar
Lorenzen, A., Pfister, G. & Mullin, T. 1982 End effects on the transition to time-dependent motion in the Taylor experiment. Phys. Fluids 26, 10–13.CrossRefGoogle Scholar
Lücke, M., Mihelcic, M., Wingerath, K. & Pfister, G. 1984 Flow in a small annulus between concentric cylinders. J. Fluid Mech. 140, 343–453.CrossRefGoogle Scholar
Malik, M., Alam, M. & Dey, J. 2006 Nonmodal energy growth and optimal perturbations in compressible plane Couette flow. Phys. Fluids 18, 034103.CrossRefGoogle Scholar
Malik, M., Dey, J. & Alam, M. 2008 Linear stability, transient energy growth, and the role of viscosity stratification in compressible plane Couette flow. Phys. Rev. E 77, 036322.CrossRefGoogle ScholarPubMed
Manela, A. & Frankel, I. 2007 On compressible Taylor–Couette problem. J. Fluid Mech. 588, 59–74.CrossRefGoogle Scholar
Marcus, P. S. 1984 Simulation of Taylor–Couette flow. Part 1. Numerical methods and comparison with experiment. J. Fluid Mech. 384, 45–64.CrossRefGoogle Scholar
Mullin, T. 1982 Mutations of steady cellular flows in the Taylor experiment. J. Fluid Mech. 121, 207–218.CrossRefGoogle Scholar
Mullin, T. & Benjamin, T. B. 1980 Transition to oscillatory motion in the Taylor experiment. Nature 288, 567–569.CrossRefGoogle Scholar
Mullin, T., Heise, M. & Pfister, G. 2017 Onset of cellular motion in Taylor–Couette flow. Phys. Rev. Fluids 2, 081901.CrossRefGoogle Scholar
Mullin, T., Pfister, G. & Lorenzen, A. 1982 New observations on hysteresis effects in Taylor–Couette flow. Phys. Fluids 25, 1134–1136.CrossRefGoogle Scholar
Mullin, T., Toya, Y. & Tavener, S. 2002 Symmetry breaking and multiplicity of states in small aspect ratio Taylor–Couette flow. Phys. Fluids 14, 2778–2787.CrossRefGoogle Scholar
Nakamura, I., Toya, Y., Yamashita, S. & Ueki, Y. 1989 An experiment on a Taylor vortex flow in a gap with a small aspect ratio: instability of Taylor vortex flows. JSME Intl J. 32 (3), 388–394.Google Scholar
Pfister, G., Schmidt, H., Cliffe, K. A. & Mullin, T. 1988 Bifurcation phenomena in Taylor–Couette flow in a very short annulus. J. Fluid Mech. 191, 1–18.CrossRefGoogle Scholar
Schaeffer, D. G. 1980 Analysis of a model in the Taylor problem. Math. Proc. Cambridge 87, 307–337.CrossRefGoogle Scholar
Synder, H. A. 1968 Stability of rotating Couette flow. I. Asymmetric waveforms. Phys. Fluids 11, 728–734.CrossRefGoogle Scholar
Taylor, G. I. 1923 Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. Lond. A 223, 289–343.Google Scholar
Taylor, G. I. 1936 a Fluid friction between rotating cylinders. I. Torque measurements. Proc. R. Soc. Lond. A 157, 546–564.Google Scholar
Taylor, G. I. 1936 b Fluid friction between rotating cylinders. II. Distribution of velocity between concentric cylinders when outer one is rotating and inner one is at rest. Proc. R. Soc. Lond. A 157, 565–578.Google Scholar
Velikhov, E. P. 1959 Stability of an ideally conducting liquid flowing between cylinders rotating in a magnetic field. Sov. Phys. JETP 36, 995–998.Google Scholar
Welsh, S., Kersal'e, E. & Jones, C. A. 2014 Compressible Taylor–Couette flow – instability mechanism and codimension-3 points. J. Fluid Mech. 750, 555–577.CrossRefGoogle Scholar
Youd, A. J. & Barenghi, C. F. 2005 Reversing and non-reversing Taylor–Couette flow at finite aspect ratio. Phys. Rev. E 72, 056321.CrossRefGoogle Scholar
Zeeman, E. C. 1976 Catastrophe theory. Sci. Am. 234, 65–83.CrossRefGoogle Scholar
Supplementary material: File

Aghor and Alam supplementary material

Aghor and Alam supplementary material

Download Aghor and Alam supplementary material(File)
File 4.6 MB