Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T18:03:09.308Z Has data issue: false hasContentIssue false
  • English
  • Français

New conservation laws of helically symmetric, plane and rotationally symmetric viscous and inviscid flows

Published online by Cambridge University Press:  13 March 2013

Olga Kelbin ,
Alexei F. Cheviakov  and
Martin Oberlack
Olga Kelbin
Affiliation:
Chair of Fluid Dynamics, TU Darmstadt, Petersenstraße 30, 64287 Darmstadt, Germany
Alexei F. Cheviakov*
Affiliation:
Department of Mathematics and Statistics, University of Saskatchewan, Saskatoon, Canada S7N 5E6
Martin Oberlack
Affiliation:
Chair of Fluid Dynamics, TU Darmstadt, Petersenstraße 30, 64287 Darmstadt, Germany Center of Smart Interfaces, TU Darmstadt, Petersenstraße 32, 64287 Darmstadt, Germany GS Computational Engineering, TU Darmstadt, Dolivostraße 15, 64293 Darmstadt, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

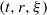Helically invariant reductions due to a reduced set of independent variables $(t, r, \xi )$ with 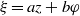$\xi = az+ b\varphi $ emerging from a cylindrical coordinate system of viscous and inviscid time-dependent fluid flow equations, with all three velocity components generally non-zero, are considered in primitive variables and in the vorticity formulation. Full sets of equations are derived. Local conservation laws of helically invariant systems are systematically sought through the direct construction method. Various new sets of conservation laws for both inviscid and viscous flows, including families that involve arbitrary functions, are derived. For both Euler and Navier–Stokes flows, infinite sets of vorticity-related conservation laws are derived. In particular, for Euler flows, we obtain a family of conserved quantities that generalize helicity. The special case of two-component flows, with zero velocity component in the invariant direction, is additionally considered, and special conserved quantities that hold for such flows are computed. In particular, it is shown that the well-known infinite set of generalized enstrophy conservation laws that holds for plane flows also holds for the general two-component helically invariant flows and for axisymmetric two-component flows.

JFM classification

Mathematical Foundations: General fluid mechanics Mathematical Foundations: Mathematical Foundations
Type
Papers
Information
Journal of Fluid Mechanics , Volume 721 , 25 April 2013 , pp. 340 - 366
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alekseenko, S. V., Kuibin, P. A., Okulov, V. L. & Shtork, S. I. 1999 Helical vortices in swirl flow. J. Fluid Mech. 382, 195–243.Google Scholar
Alekseenko, S. V. & Okulov, V. L. 1996 Swirl flow in technical applications (review). Thermophys. Aeromech. 3, 97–128.Google Scholar
Anco, S. C. & Bluman, G. W. 2002a Direct construction method for conservation laws of partial differential equations. Part I: Examples of conservation law classifications. Eur. J. Appl. Math. 13, 545–566.CrossRefGoogle Scholar
Anco, S. C. & Bluman, G. W. 2002b Direct construction method for conservation laws of partial differential equations. Part II: General treatment. Eur. J. Appl. Math 13, 567–585.Google Scholar
Anco, S. C., Bluman, G. W. & Cheviakov, A. F. 2010 Applications of Symmetry Methods to Partial Differential Equations. Applied Mathematical Sciences, vol. 168, Springer.Google Scholar
Anco, S., Bluman, G. & Wolf, T. 2008 Invertible mappings of nonlinear PDES to linear PDES through admitted conservation laws. Acta Appl. Math. 101 (1), 21–38.Google Scholar
Batchelor, G. K. 2000 An Introduction to Fluid Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Benjamin, T. B. 1972 The stability of solitary waves. Proc. R. Soc. Lond. A 328 (1573), 153–183.Google Scholar
Bluman, G., Cheviakov, A. F. & Ganghoffer, J.-F. 2008 Non-locally related PDE systems for one-dimensional nonlinear elastodynamics. J. Engng Maths 62 (3), 203–221.Google Scholar
Bogoyavlenskij, O. I. 2000 Helically symmetric astrophysical jets. Phys. Rev. E 62, 8616–8627.Google Scholar
Bowman, J. C. 2009 Casimir cascades in two-dimensional turbulence. In Advances in Turbulence XII, pp. 685–688.Google Scholar
Caviglia, G. & Morro, A. 1987 Noether-type conservation laws for perfect fluid motions. J. Math. Phys. 28 (5), 1056–1060.Google Scholar
Caviglia, G. & Morro, A. 1989 Conservation laws for incompressible fluids. Intl J. Maths Math. Sci. 12 (2), 377–384.CrossRefGoogle Scholar
Chandrsuda, C., Mehta, R. D., Weir, A. D. & Bradshaw, P. 1978 Effect of free stream turbulence on large structure in turbulent mixing layers. J. Fluid Mech. 85 (04), 693–704.Google Scholar
Cheviakov, A. F. 2007 Gem software package for computation of symmetries and conservation laws of differential equations. Comput. Phys. Commun. 176 (1), 48–61.CrossRefGoogle Scholar
Cheviakov, A. F. & Bogoyavlenskij, O. I. 2004 Exact anisotropic mhd equilibria. J. Phys. A: Math. General 37 (30), 7593.Google Scholar
Dritschel, D. G. 1991 Generalized helical Beltrami flows in hydrodynamics and magnethydrodynamics. J. Fluid Mech. 222, 525–541.Google Scholar
Ettinger, B. S. & Titi, E. 2009 Global existence and uniqueness of weak solutions of 3-d Euler equations with helical symmetry in the absence of vorticity stretching. SIAM J. Math. Anal. 41 (1), 269–296.Google Scholar
Frewer, M., Oberlack, M. & Guenther, S. 2007 Symmetry investigations on the incompressible stationary axisymmetric euler equations with swirl. Fluid Dyn. Res. 39 (8), 647.Google Scholar
Germano, M. 1982 On the effect of torsion on a helical pipe flow. J. Fluid Mech. 125, 1–8.Google Scholar
Germano, M. 1989 The dean equations extended to a helical pipe flow. J. Fluid Mech. 203, 289–305.Google Scholar
Gupta, A. & Kumar, R. 2007 Three-dimensional turbulent swirling flow in a cylinder: experiments and computations. Intl J. Heat Fluid Flow 28 (2), 249–261.CrossRefGoogle Scholar
Johnson, J. L., Oberman, C. R., Kulsrud, R. M. & Frieman, E. A. 1958 Some stable hydromagnetic equilibria. Phys. Fluids 1 (4), 281–296.Google Scholar
Knops, R. J. & Stuart, C. A. 1984 Quasiconvexity and uniqueness of equilibrium solutions in nonlinear elasticity. Arch. Rat. Mech. Anal. 86 (3), 233–249.Google Scholar
Kubitschek, J. P. & Weidman, P. D. 2008 Helical instability of a rotating viscous liquid jet. Phys. Fluids 20 (9), 091104.Google Scholar
Landman, M. J. 1990a On the generation of helical waves in circular pipe flow. Phys. Fluids 2 (5), 738–747.Google Scholar
Landman, M. J. 1990b Time-dependent helical waves in rotating pipe flow. J. Fluid Mech. 221, 289–310.Google Scholar
Lax, P. D. 1968 Integrals of nonlinear equations of evolution and solitary waves. Commun. Pure Appl. Maths 21 (5), 467–490.CrossRefGoogle Scholar
Mahalov, A., Titi, E. S. & Leibovich, S. 1990 Invariant helical subspaces for the Navier–Stokes equations. Arch. Rat. Mech. Anal. 112 (3), 193–222.CrossRefGoogle Scholar
Mitchell, A., Morton, S. & Forsythe, J. 1997 Wind turbine wake aerodynamics. Air Force Academy Colorado Springs, Dept. of Aeronautics, Report ADA425027.Google Scholar
Moffatt, H. K. 1969 The degree of knottedness of tangled vortex lines. J. Fluid Mech. 35 (01), 117–129.CrossRefGoogle Scholar
Moiseev, S. S., Sagdeev, R. Z., Tur, A. V. & Yanovskii, V. V. 1982 Freezing-in integrals and lagrange invariants in hydrodynamic models. Sov. Phys.-JETP (Engl. Transl.) 56 (1), 117–123.Google Scholar
Sarpkaya, T. 1971 On stationary and travelling vortex breakdowns. J. Fluid Mech. 45 (03), 545–559.CrossRefGoogle Scholar
Satoru, I. 1989 An experimental study on extinction and stability of tubular flames. Combust. Flame 75 (3–4), 367–379.Google Scholar
Schnack, D. D., Caramana, E. J. & Nebel, R. A. 1985 Three-dimensional magnetohydrodynamic studies of the reversed-field pinch. Phys. Fluids 28 (1), 321–333.CrossRefGoogle Scholar
Toplosky, N. & Akylas, T. R. 1988 Nonlinear spiral waves in rotating pipe flow. J. Fluid Mech. 190, 39–54.Google Scholar
Tur, A. V. & Yanovsky, V. V. 1993 Invariants in dissipationless hydrodynamic media. J. Fluid Mech. 248, 67–106.Google Scholar
Tuttle, E. R. 1990 Laminar flow in twisted pipes. J. Fluid Mech. 219, 545–570.Google Scholar
Vermeer, L. J., Sorensen, J. N. & Crespo, A. 2003 Wind turbine wake aerodynamics. Prog. Aerosp. Sci. 39 (6–7), 467–510.CrossRefGoogle Scholar
Volkov, D. V., Tur, A. V. & Yanovsky, V. V. 1995 Hidden supersymmetry of classical systems (hydrodynamics and conservation laws). Phys. Lett. A 203 (5), 357–361.CrossRefGoogle Scholar
Wang, C. Y. 1981 On the low-Reynolds-number flow in a helical pipe. J. Fluid Mech. 108, 185–194.Google Scholar
Zabielski, L. & Mestel, A. J. 1998 Steady flow in a helically symmetric pipe. J. Fluid Mech. 370, 297–320.Google Scholar