Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-12-01T03:51:43.722Z Has data issue: false hasContentIssue false
  • English
  • Français

Near-wall turbulent fluctuations in the absence of wide outer motions

Published online by Cambridge University Press:  16 April 2013

Yongyun Hwang
Yongyun Hwang*
Affiliation:
Laboratoire d’Hydrodynamique (LadHyX), CNRS École Polytechnique, 91128 Palaiseau, France
*
†Present address: Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge CB3 0WA, UK. Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

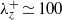Numerical experiments that remove turbulent motions wider than ${ \lambda }_{z}^{+ } \simeq 100$ are carried out up to 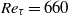${\mathit{Re}}_{\tau } = 660$ in a turbulent channel. The artificial removal of the wide outer turbulence is conducted with spanwise minimal computational domains and an explicit filter that effectively removes spanwise uniform eddies. The mean velocity profile of the remaining motions shows very good agreement with that of the full simulation below 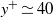${y}^{+ } \simeq 40$, and the near-wall peaks of the streamwise velocity fluctuation scale very well in the inner units and remain almost constant at all the Reynolds numbers considered. The self-sustaining motions narrower than 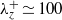${ \lambda }_{z}^{+ } \simeq 100$ generate smaller turbulent skin friction than full turbulent motions, and their contribution to turbulent skin friction gradually decays with the Reynolds number. This finding suggests that the role of the removed outer structures becomes increasingly important with the Reynolds number; thus one should aim to control the large scales for turbulent drag reduction at high Reynolds numbers. In the near-wall region, the streamwise and spanwise velocity fluctuations of the motions of 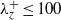${ \lambda }_{z}^{+ } \leq 100$ reveal significant lack of energy at long streamwise lengths compared to those of the full simulation. In contrast, the losses of the wall-normal velocity and the Reynolds stress are not as large as those of these two variables. This implies that the streamwise and spanwise velocities of the removed motions penetrate deep into the near-wall region, while the wall-normal velocity and the Reynolds stress do not.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 723 , 25 May 2013 , pp. 264 - 288
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H., Kawamura, H. & Choi, H. 2004 Very large-scale structures and their effects on the wall shear-stress fluctuations in a turbulent channel flow up to $Re= 640$ . J. Fluid Engng 126, 835–843.Google Scholar
Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.Google Scholar
del Álamo, J. C. & Jiménez, J. 2003 Spectra of the very large anisotropic scales in turbulent channels. Phys. Fluids 15, L41–L44.Google Scholar
del Álamo, J. C. & Jiménez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.CrossRefGoogle Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.Google Scholar
Butler, K. M. & Farrell, B. F. 1993 Optimal perturbations and streak spacing in wall-bounded turbulent shear flow. Phys. Fluids 5, 774–777.Google Scholar
Chang, Y., Collis, S. S. & Ramakrishnan, S. 2002 Viscous effects in control of near-wall turbulence. Phys. Fluids 14 (11), 4069–4080.CrossRefGoogle Scholar
Choi, H., Moin, P. & Kim, J. 1994 Active turbulence control for drag reduction in wall-bounded flows. J. Fluid Mech. 262, 75–110.Google Scholar
Cossu, C., Pujals, G. & Depardon, S. 2009 Optimal transient growth and very large-scale structures in turbulent boundary layers. J. Fluid Mech. 619, 79–94.Google Scholar
De Graaff, D. B. & Eaton, J. K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.CrossRefGoogle Scholar
Dean, R. B. 1978 Reynolds number dependence of skin friction and other bulk flow variables in two-dimensional rectangular duct flow. Trans. ASME: J. Fluids Engng 100, 215–233.Google Scholar
Faisst, H. & Eckhardt, B. 2003 Travelling waves in pipe flow. Phys. Rev. Lett. 91, 224502.Google Scholar
Flores, O. & Jiménez, J 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22, 071704.Google Scholar
Ganapathisubramani, B., Hutchins, N., Hambleton, W. T., Longmire, E. K. & Marusic, I. 2005 Investigation of large-scale coherence in a turbulent boundary layer using two-point correlation. J. Fluid Mech. 524, 57–80.CrossRefGoogle Scholar
Gayme, D. F., McKeon, B. J., Bamieh, B., Papachristodoulou, A. & Doyle, J. C. 2011 Amplification and nonlinear mechanisms in plane Couette flow. Phys. Fluids 23, 065108.Google Scholar
Gayme, D. F., McKeon, B. J., Papachristodoulou, A., Bamieh, B. & Doyle, J. C. 2010 A streamwise constant model of turbulence in plane Couette flow. J. Fluid Mech. 665, 99–119.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanovic, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.Google Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech 287, 317–348.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to $R{e}_{\tau } = 2003$ . Phys. Fluids 18, 011702.Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hwang, Y. & Cossu, C. 2010a Amplification of coherent streaks in the turbulent Couette flow: an input–output analysis at low Reynolds number. J. Fluid Mech. 643, 333–348.Google Scholar
Hwang, Y. & Cossu, C. 2010b Linear non-normal energy amplification of harmonic and stochastic forcing in the turbulent channel flow. J. Fluid Mech. 664, 51–73.Google Scholar
Hwang, Y. & Cossu, C. 2010c Self-sustained process at large scales in turbulent channel flow. Phys. Rev. Lett. 105, 044505.CrossRefGoogle ScholarPubMed
Hwang, Y. & Cossu, C. 2011 Self-sustained processes in the logarithmic layer of turbulent channel flows. Phys. Fluid 23, 061702.CrossRefGoogle Scholar
Jeong, J., Benney, F., Schoppa, W. & Kim, J. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.Google Scholar
Jiménez, J., del Álamo, J. C. & Flores, O. 2004 The large-scale dynamics of near-wall turbulence. J. Fluid Mech. 505, 179–199.CrossRefGoogle Scholar
Jiménez, J. & Hoyas, S. 2008 Turbulent fluctuations above the buffer layer of wall-bounded flows. J. Fluid Mech. 611, 215–236.CrossRefGoogle Scholar
Jiménez, J., Kawahara, G., Simens, M. P., Nagata, M. & Shiba, M. 2005 Phys. Fluids 17, 015105.CrossRefGoogle Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.Google Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.Google Scholar
Jovanović, M. R. & Bamieh, B. 2005 Componentwise energy amplification in channel flow. J. Fluid Mech. 543, 145–183.Google Scholar
Karniadiakis, G. E. & Choi, K. S. 2003 Mechanisms on transverse motions in turbulent wall flows. Annu. Rev. Fluid Mech. 35, 45–62.Google Scholar
Kasagi, N., Suzuki, Y. & Fukagata, K. 2008 Microelectromechanical systems based feedback control of turbulence for skin friction reduction. Annu. Rev. Fluid Mech. 41, 231–251.Google Scholar
Kim, J. & Moin, P 1985 Application of a fractional-step method to incompressible Navier–Stokes equations. J. Comput. Phys. 59, 308–323.Google Scholar
Kim, J., Moin, P. & Moser, R. D. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.Google Scholar
Kravchenko, A. G., Choi, H. & Moin, P. 1993 On the relation of near-wall streamwise vortices to wall skin friction in turbulent boundary layers. Phys. Fluids A 5, 3307–3309.Google Scholar
Landahl, M. T. 1990 On sublayer streaks. J. Fluid Mech. 212, 593–614.CrossRefGoogle Scholar
Marusic, I. & Kunkel, G. J. 2003 Streamwise turbulent intensity formulation for flat-plate boundary layers. Phys. Fluids 15 (8), 2461–2464.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010a Predictive model for wall-bounded turbulent flow. Science 329, 193–196.Google Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010b Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22, 065103.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boudnary layers. J. Fluid. Mech. 628, 311–337.Google Scholar
Mathis, R., Marusic, I., Chernyshenko, S. I. & Hutchins, N. 2013 Estimating wall-shear-stress fluctuations given an outer region input. J. Fluid. Mech. 715, 163–180.Google Scholar
Metzger, M. M. & Klewicki, J. C. 2001 A comparative study of near-wall turbulence in high and low Reynolds number boundary layers. Phys. Fluids 13, 692–701.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to $R{e}_{\tau } = 590$ . Phys. Fluids 11, 943–945.Google Scholar
Orlandi, P. & Jimenez, J. 1994 On the generation of turbulent wall friction. Phys. Fluids 6, 634–641.Google Scholar
Park, J., Hwang, Y. & Cossu, C. 2011 On the stability of large-scale streaks in the turbulent Couette and Poiseulle flows. C. R. Méc. 339 (1), 1–5.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of turbulence. J. Fluid Mech. 119, 173–217.Google Scholar
Perry, A. E., Henbest, S. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.Google Scholar
Pujals, G., García-Villalba, M., Cossu, C. & Depardon, S. 2009 A note on optimal transient growth in turbulent channel flows. Phys. Fluids 21, 015109.Google Scholar
Ricco, P. & Quadrio, M. 2008 Wall-oscillation conditions for drag reduction in turbulent channel flow. Intl J. Heat Fluid Flow 29 (4), 891–902.Google Scholar
Saikrishnan, N., De Angelis, E., Longmire, E. K., Marusic, I., Casciola, C. M. & Piva, R. 2012 Reynolds number effects on scale energy balance in wall turbulence. Phys. Fluids 23, 015101.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Schoppa, S. & Hussain, F. 1998 A large-scale control strategy for drag reduction in turbulent boundary layers. Phys. Fluids 10, 1049–1051.Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.Google Scholar
Smith, J. R. & Metzler, S. P. 1983 The characteristics of low-speed streaks in the near-wall region of a turbulent boundary layer. J. Fluid Mech. 129, 27–54.Google Scholar
Toh, S. & Itano, T. 2005 Interaction between a large-scale structure and near-wall structures in channel flow. J. Fluid Mech. 524, 249–262.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2005 Energetic spanwise modes in the logarithmic layer of a turbulent boundary layer. J. Fluid Mech. 545, 141–162.Google Scholar
Touber, E. & Leschziner, M. A. 2012 Near-wall streak modification by spanwise oscillatory wall motion and drag-reduction mechanisms. J. Fluid Mech. 693, 150–200.Google Scholar
Townsend, A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.Google Scholar
Waleffe, F. 1998 Three-dimensional coherent states in plane shear flows. Phys. Rev. Lett. 81, 4140–4143.CrossRefGoogle Scholar
Waleffe, F. 2001 Exact coherent structures in channel flow. J. Fluid Mech. 435, 93–102.Google Scholar
Waleffe, F. 2003 Homotopy of exact coherent structures in plane shear flows. Phys. Fluids 15, 1517–1534.Google Scholar
Wedin, H. & Kerswell, R. R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J. Fluid Mech. 508, 333–371.Google Scholar
Willis, A. P., Hwang, Y. & Cossu, C. 2010 Optimally amplified large-scale streaks and drag reduction in the turbulent pipe flow. Phys. Rev. E 82, 036321.Google Scholar