Published online by Cambridge University Press: 22 March 2017
We investigate theoretically and numerically the modulation of near-inertial waves by a larger-amplitude geostrophically balanced mean flow. Because the excited wave is initially trapped in the mixed layer, it projects onto a broad spectrum of vertical modes, each mode
 $n$
being characterized by a Burger number,
$n$
being characterized by a Burger number,
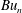 $Bu_{n}$
, proportional to the square of the vertical scale of the mode. Using numerical simulations of the hydrostatic Boussinesq equations linearized about a prescribed balanced background flow, we show that the evolution of the wave field depends strongly on the spectrum of
$Bu_{n}$
, proportional to the square of the vertical scale of the mode. Using numerical simulations of the hydrostatic Boussinesq equations linearized about a prescribed balanced background flow, we show that the evolution of the wave field depends strongly on the spectrum of
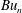 $Bu_{n}$
relative to the Rossby number of the balanced flow,
$Bu_{n}$
relative to the Rossby number of the balanced flow,
 $\unicode[STIX]{x1D716}$
, with smaller relative
$\unicode[STIX]{x1D716}$
, with smaller relative
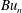 $Bu_{n}$
leading to smaller horizontal scales in the wave field, faster accumulation of wave amplitude in anticyclones and faster propagation of wave energy into the deep ocean. This varied behaviour of the wave may be understood by considering the dynamics in each mode separately; projecting the linearized hydrostatic Boussinesq equations onto modes yields a set of linear shallow water equations, with
$Bu_{n}$
leading to smaller horizontal scales in the wave field, faster accumulation of wave amplitude in anticyclones and faster propagation of wave energy into the deep ocean. This varied behaviour of the wave may be understood by considering the dynamics in each mode separately; projecting the linearized hydrostatic Boussinesq equations onto modes yields a set of linear shallow water equations, with
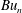 $Bu_{n}$
playing the role of the reduced gravity. The wave modes fall into two asymptotic regimes, defined by the scalings
$Bu_{n}$
playing the role of the reduced gravity. The wave modes fall into two asymptotic regimes, defined by the scalings
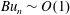 $Bu_{n}\sim O(1)$
for low modes and
$Bu_{n}\sim O(1)$
for low modes and
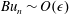 $Bu_{n}\sim O(\unicode[STIX]{x1D716})$
for high modes. An amplitude equation derived for the former regime shows that vertical propagation is weak for low modes. The high-mode regime is the basis of the Young & Ben Jelloul (J. Mar. Res., vol. 55, 1997, pp. 735–766) theory. This theory is here extended to
$Bu_{n}\sim O(\unicode[STIX]{x1D716})$
for high modes. An amplitude equation derived for the former regime shows that vertical propagation is weak for low modes. The high-mode regime is the basis of the Young & Ben Jelloul (J. Mar. Res., vol. 55, 1997, pp. 735–766) theory. This theory is here extended to
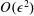 $O(\unicode[STIX]{x1D716}^{2})$
, from which amplitude equations for the subregimes
$O(\unicode[STIX]{x1D716}^{2})$
, from which amplitude equations for the subregimes
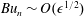 $Bu_{n}\sim O(\unicode[STIX]{x1D716}^{1/2})$
and
$Bu_{n}\sim O(\unicode[STIX]{x1D716}^{1/2})$
and
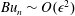 $Bu_{n}\sim O(\unicode[STIX]{x1D716}^{2})$
are derived. The accuracy of each approximation is demonstrated by comparing numerical solutions of the respective amplitude equation to simulations of the linearized shallow water equations in the same regime. We emphasize that since inertial wave energy and shear are distributed across vertical modes, their overall modulation is due to the collective behaviour of the wave field in each regime. A unified treatment of these regimes is a novel feature of this work.
$Bu_{n}\sim O(\unicode[STIX]{x1D716}^{2})$
are derived. The accuracy of each approximation is demonstrated by comparing numerical solutions of the respective amplitude equation to simulations of the linearized shallow water equations in the same regime. We emphasize that since inertial wave energy and shear are distributed across vertical modes, their overall modulation is due to the collective behaviour of the wave field in each regime. A unified treatment of these regimes is a novel feature of this work.