Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2025-01-02T19:42:17.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Near-inertial parametric subharmonic instability of internal wave beams in a background mean flow

Published online by Cambridge University Press:  01 February 2021

Boyu Fan Open the ORCID record for Boyu Fan [Opens in a new window]  and
T.R. Akylas
Boyu Fan
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA02139, USA
T.R. Akylas*
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA02139, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

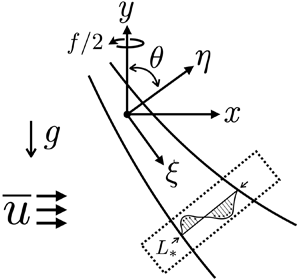
The effect of a small background constant horizontal mean flow on the parametric subharmonic instability (PSI) of locally confined internal wave beams is discussed for the case where the beam frequency is close to twice the inertial frequency due to background rotation. Under this condition, PSI is particularly potent because of the vanishing of the group velocity at the inertial frequency, which prolongs contact of near-inertial subharmonic perturbations with the primary wave. The mean flow generally stabilizes the very short-scale limit of such perturbations. By contrast, the stability of longer-scale perturbations hinges on the strength and the direction of the mean flow; particularly, a negative mean flow (antiparallel to the horizontal projection of the beam group velocity) can extend the sub-inertial range of PSI. However, a large enough mean flow of either sign ultimately weakens PSI.

JFM classification

Geophysical and Geological Flows: Internal waves
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 911 , 25 March 2021 , R3
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alford, M.H., MacKinnon, J.A., Zhao, Z., Pinkel, R., Klymak, J. & Peacock, T. 2007 Internal waves across the pacific. Geophys. Res. Lett. 34 (24), L24601.CrossRefGoogle Scholar
Bourget, B., Scolan, H., Dauxois, T., Le Bars, M., Odier, P. & Joubaud, S. 2014 Finite-size effects in parametric subharmonic instability. J. Fluid Mech. 759, 739–750.CrossRefGoogle Scholar
Dauxois, T., Joubaud, S., Odier, P. & Venaille, A. 2018 Instabilities of internal gravity wave beams. Annu. Rev. Fluid Mech. 50 (1), 131–156.CrossRefGoogle Scholar
Fan, B. & Akylas, T.R. 2019 Effect of background mean flow on PSI of internal wave beams. J. Fluid Mech. 869, R1.CrossRefGoogle Scholar
Fan, B. & Akylas, T.R. 2020 Instabilities of finite-width internal wave beams: from Floquet analysis to PSI. J. Fluid Mech. (in press).CrossRefGoogle Scholar
Hazewinkel, J. & Winters, K.B. 2011 PSI of the internal tide on a $\beta$ plane: flux divergence and near-inertial wave propagation. J. Phys. Oceanogr. 41 (9), 1673–1682.CrossRefGoogle Scholar
Hibiya, T., Nagasawa, M. & Niwa, Y. 2002 Nonlinear energy transfer within the oceanic internal wave spectrum at mid and high latitudes. J. Geophys. Res. Oceans 107 (C11), 3207.CrossRefGoogle Scholar
Johnston, T.M.S., Rudnick, D.L., Carter, G.S., Todd, R.E. & Cole, S.T. 2011 Internal tidal beams and mixing near monterey bay. J. Geophys. Res. 116, C03017.CrossRefGoogle Scholar
Karimi, H.H. & Akylas, T.R. 2014 Parametric subharmonic instability of internal waves: locally confined beams versus monochromatic wavetrains. J. Fluid Mech. 757, 381–402.CrossRefGoogle Scholar
Karimi, H.H. & Akylas, T.R. 2017 Near-inertial parametric subharmonic instability of internal wave beams. Phys. Rev. Fluids 2 (7), 074801.CrossRefGoogle Scholar
Lamb, K.G. 2004 Nonlinear interaction among internal wave beams generated by tidal flow over supercritical topography. Geophys. Res. Lett. 31 (9), L09313.CrossRefGoogle Scholar
MacKinnon, J.A., Alford, M.H., Sun, O., Pinkel, R., Zhao, Z. & Klymak, J. 2013 Parametric subharmonic instability of the internal tide at $29^{\circ }\textrm {N}$. J. Phys. Oceanogr. 43 (1), 17–28.CrossRefGoogle Scholar
MacKinnon, J.A. & Winters, K.B. 2005 Subtropical catastrophe: significant loss of low-mode tidal energy at $28.9^{\circ }$. Geophys. Res. Lett. 32 (15), L15605.CrossRefGoogle Scholar
Peacock, T., Echeverri, P. & Balmforth, N.J. 2008 An experimental investigation of internal tide generation by two-dimensional topography. J. Phys. Oceanogr. 38 (1), 235–242.CrossRefGoogle Scholar
Richet, O., Muller, C. & Chomaz, J.-M. 2017 Impact of a mean current on the internal tide energy dissipation at the critical latitude. J. Phys. Oceanogr. 47 (6), 1457–1472.CrossRefGoogle Scholar
Staquet, C. & Sommeria, J. 2002 Internal gravity waves: from instabilities to turbulence. Annu. Rev. Fluid Mech. 34 (1), 559–593.CrossRefGoogle Scholar
Sutherland, B.R. 2013 The wave instability pathway to turbulence. J. Fluid Mech. 724, 1–4.CrossRefGoogle Scholar
Tabaei, A. & Akylas, T.R. 2003 Nonlinear internal gravity wave beams. J. Fluid Mech. 482, 141–161.CrossRefGoogle Scholar
Yang, W., Hibiya, T., Tanaka, Y., Zhao, L. & Wei, H. 2018 Modification of parametric subharmonic instability in the presence of background geostrophic currents. Geophys. Res. Lett. 45 (23), 12957–12962.CrossRefGoogle Scholar
Yang, W., Wei, H. & Zhao, L. 2020 Parametric subharmonic instability of the semidiurnal internal tides at the East China Sea shelf slope. J. Phys. Oceanogr. 50 (4), 907–920.CrossRefGoogle Scholar
Young, W.R., Tsang, Y.-K. & Balmforth, N.J. 2008 Near-inertial parametric subharmonic instability. J. Fluid Mech. 607, 25–49.CrossRefGoogle Scholar