Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T11:01:49.249Z Has data issue: false hasContentIssue false
  • English
  • Français

Naturally bounded plumes

Published online by Cambridge University Press:  01 February 2013

Rabah Mehaddi ,
Fabien Candelier  and
Olivier Vauquelin
Rabah Mehaddi*
Affiliation:
Laboratoire IUSTI, UMR CNRS 7343, Aix-Marseille Université, 5 rue Enrico Fermi, 13 453 Marseille CEDEX 13, France
Fabien Candelier
Affiliation:
Laboratoire IUSTI, UMR CNRS 7343, Aix-Marseille Université, 5 rue Enrico Fermi, 13 453 Marseille CEDEX 13, France
Olivier Vauquelin
Affiliation:
Laboratoire IUSTI, UMR CNRS 7343, Aix-Marseille Université, 5 rue Enrico Fermi, 13 453 Marseille CEDEX 13, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper investigates theoretically the vertical evolution of a turbulent plume into a linearly stratified ambient fluid, by regarding it as composed of two distinct regions. In the first region, called the positive buoyant region, the plume buoyancy and the plume momentum act in the same upward direction, whereas in the second region, called the negative buoyant region, they act in opposite directions. In a first step, analytical expressions for the plume variables at the transition height (i.e. between the two regions) are obtained from one-dimensional conservation equations, using the plume entrainment model and under the Boussinesq approximation. In a second step, these variables are used in order to determine analytically the buoyancy and volume fluxes as well as the density deficit of the plume at its top. In this investigation, the transition height (denoted 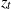${z}_{t} $) and the total plume height (denoted 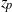${z}_{p} $) are obtained in the form of two integrals. These integrals are evaluated asymptotically in three different cases associated with particular flow regimes. Finally, the limit of the Boussinesq assumption for such flows is discussed.

JFM classification

Convection: Convection Geophysical and Geological Flows: Geophysical and Geological Flows Convection: Plumes/thermals
Type
Papers
Information
Journal of Fluid Mechanics , Volume 717 , 25 February 2013 , pp. 472 - 483
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abraham, G. & Eysink, W. D. 1969 Jets issuing into fluid with a density gradient. Delft Hydraul. Lab. Publ. 66, 145–175.Google Scholar
Bloomfield, L. J. & Kerr, R. C. 1998 Turbulent fountains in a stratified fluid. J. Fluid Mech. 358, 335–356.CrossRefGoogle Scholar
Briggs, G. A. 1969. Plume Rise. US Atomic Energy Commission Critical Review Series.Google Scholar
Caulfield, C. P. & Woods, A. W. 1998 Turbulent gravitational convection from a point source in a non-uniformly stratified environment. J. Fluid Mech. 360, 229–248.CrossRefGoogle Scholar
Carazzo, G., Kaminski, E. & Tait, S. 2008 On the rise of turbulent plumes: quantitative effects of variable entrainment for submarine hydrothermal vents, terrestrial and extra terrestrial explosive volcanism. J. Geophys. Res. 113, B09201.Google Scholar
Devenish, B. J., Rooney, G. G. & Thomson, D. J. 2010 Large-eddy simulation of a buoyant plume in uniform and stably stratified environments. J. Fluid Mech. 652, 75–103.CrossRefGoogle Scholar
Fan, L. 1967. Turbulent buoyant jets into stratified or flowing ambient fluids. Report KH-R-15, California Inst. of Technology, Pasadena, California, USA.Google Scholar
Fannelop, T. K. & Webber, D. M. 2003 On buoyant plumes from area sources in a calm environment. J. Fluid Mech. 497, 319–334.CrossRefGoogle Scholar
Head, J. & Wilson, L. 2003 Deep submarine pyroclastic eruptions: theory and predicted landforms and deposits. J. Volcanol. Geotherm. Res. 121, 155–193.CrossRefGoogle Scholar
Hunt, G. R. & Kaye, N. B. 2005 Lazy plumes. J. Fluid Mech. 533, 329–338.CrossRefGoogle Scholar
Kaminski, E., Chenet, A. L., Jaupart, C. & Courtillot, V. 2011 Rise of volcanic plumes to the stratosphere aided by penetrative convection above large lava flows. Earth Planet. Sci. Lett. 301, 171–178.CrossRefGoogle Scholar
Kaminski, E., Tait, S. & Carazzo, G. 2005 Turbulent entrainment in jets with arbitrary buoyancy. J. Fluid Mech. 526, 361–376.CrossRefGoogle Scholar
Kaye, N. B. 2008 Turbulent plumes in stratified environments: a review of recent work. Atmos. Ocean 46 (4), 433–441.CrossRefGoogle Scholar
Kaye, N. B. & Scase, M. M. 2011 Straight-sided solutions to classical and modified plume flux equations. J. Fluid Mech. 680, 564–573.CrossRefGoogle Scholar
Malin, M. R. 1989 Analysis of turbulent forced plumes into a stable environment. Appl. Math. Model. 13, 122–126.CrossRefGoogle Scholar
Mehaddi, R., Vauquelin, O. & Candelier, F. 2012 Analytical solutions for Boussinesq fountains in a linearly stratified environment. J. Fluid Mech. 691, 487–497.CrossRefGoogle Scholar
Michaux, G. & Vauquelin, O. 2008 Solutions for turbulent buoyant plumes rising from circular sources. Phys. Fluids 20, 066601.CrossRefGoogle Scholar
Morton, B. R., Taylor, G. I. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234, 1–23.Google Scholar
Scase, M. M., Caulfield, C. P. & Dalziel, S. B. 2006 Boussinesq plumes and jets with decreasing source strengths in stratified environments. J. Fluid Mech. 563, 463–472.CrossRefGoogle Scholar
Sneck, H. J. & Brown, D. H. 1974 Plume rise from large thermal sources such as dry cooling towers. Tans. ASME: J. Heat Transfer 96, 232–238.CrossRefGoogle Scholar
Speer, K. G. & Rona, P. A. 1989 A model of an Atlantic and Pacific hydrothermal plume. J. Geophys. Res. 94, 6213–6220.CrossRefGoogle Scholar
Suzuki, Y. J., Koyaguchi, T., Ogawa, M. & Hachisu, I. 2005 A numerical study of turbulent behaviour in eruption clouds using a 3-D fluid-dynamics model. J. Geophys. Res. 110, B08201.Google Scholar
Turner, J. S. 1986 Turbulent entrainment: the development of the entrainment assumption, and its application to geophysical flows. J. Fluid Mech. 173, 431–471.CrossRefGoogle Scholar
Woods, A. W. 1995 The dynamics of explosive volcanic eruptions. Rev. Geophys. 33 (4), 495–530.CrossRefGoogle Scholar
Woods, A. W. 1997 A note on non-Boussinesq plumes in an incompressible stratified environment. J. Fluid Mech. 345, 347–356.CrossRefGoogle Scholar
Woods, A. W. 2010 Turbulent plumes in nature. Annu. Rev. Fluid Mech. 42, 391–412.CrossRefGoogle Scholar