Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T14:52:05.208Z Has data issue: false hasContentIssue false
  • English
  • Français

Natural convection and thermal drift

Published online by Cambridge University Press:  08 August 2017

Arman Abtahi Open the ORCID record for Arman Abtahi [Opens in a new window]  and
J. M. Floryan Open the ORCID record for J. M. Floryan [Opens in a new window]
Arman Abtahi*
Affiliation:
Department of Mechanical and Materials Engineering, University of Western Ontario, London, Ontario, N6A 5B9, Canada
J. M. Floryan
Affiliation:
Department of Mechanical and Materials Engineering, University of Western Ontario, London, Ontario, N6A 5B9, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An analysis of natural convection in a horizontal, geometrically non-uniform slot exposed to spatially non-uniform heating has been carried out. The upper plate is smooth and isothermal, and the lower plate has sinusoidal corrugations with a sinusoidal temperature distribution. The distributions of the non-uniformities are characterized in terms of the wavenumber $\unicode[STIX]{x1D6FC}$ and their relative position is expressed in terms of the phase difference 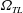$\unicode[STIX]{x1D6FA}_{TL}$. The analysis is limited to heating conditions which do not give rise to secondary motions in the absence of the non-uniformities. The heating creates horizontal temperature gradients which lead to the formation of vertical and horizontal pressure gradients which drive the motion regardless of the intensity of the heating. When the hot spots (points of maximum temperature) overlap either with the corrugation tips or with the corrugation bottoms, convection assumes the form of pairs of counter-rotating rolls whose size is dictated by the heating/corrugation wavelengths. The formation of a net horizontal flow, referred to as thermal drift, is observed for all other relative positions of the hot spots and corrugation tips. Both periodic heating as well as periodic corrugations are required for the formation of this drift, which can be directed in the positive as well as in the negative horizontal directions depending on the phase difference between the heating and corrugation patterns. The most intense convection and the largest drift occur for wavelengths comparable to the slot height, and their intensities increase proportionally to the heating intensity as well as proportionally to the corrugation amplitude, with the drift being a very strong function of the phase difference. Convection creates forces at the plates which would cause horizontal displacement of the corrugated plate and deform the corrugations if such effects were allowed. Tangential forces generated by the uniform heating always contribute to the corrugation buildup while similar forces generated by the periodic heating contribute to the buildup only when the hot spots overlap with the upper part of the corrugation. 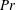The processes described above are qualitatively similar for all Prandtl numbers $Pr$, with the intensity of convection and the magnitude of the drift increasing with a reduction in $Pr$.

JFM classification

Convection: Convection Flow Control: Flow Control
Type
Papers
Information
Journal of Fluid Mechanics , Volume 826 , 10 September 2017 , pp. 553 - 582
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abtahi, A. & Floryan, J. M. 2017 Natural convection in corrugated slots. J. Fluid Mech. 815, 537–569.Google Scholar
Abtahi, A., Hossain, M. Z. & Floryan, J. M. 2016 Spectrally accurate algorithm for analysis of convection in corrugated conduits. Comput. Maths Applics. 72, 2636–2659.Google Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
Asgarian, A., Hossain, M. Z. & Floryan, J. M. 2016 Rayleigh–Bénard convection driven by a long wavelength heating. J. Theor. Comput. Fluid Mech. 30, 313–337.Google Scholar
Beltrame, P., Knobloch, E., Hänggi, P. & Thiele, U. 2011 Rayleigh and depinning instabilities of forced liquid ridges on heterogeneous substrates. Phys. Rev. E 83, 016305.Google Scholar
Bénard, H. 1900 Les tourbillons cellulaires dans une nappe liquide. Revue Générale Science Pure et Applique 11, 1261–1271.Google Scholar
Bodenschatz, E., Pesch, W. & Ahlers, G. 2000 Recent developments in Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 32, 709–778.CrossRefGoogle Scholar
Busse, F. H. & Clever, R. M. 1979 Instabilities of convection rolls in a fluid of moderate Prandtl number. J. Fluid Mech. 91, 319–335.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Oxford University Press.Google Scholar
Chilla, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 58–82.Google ScholarPubMed
Clever, R. M. & Busse, F. H. 1974 Transition to time-dependent convection. J. Fluid Mech. 65, 625–645.Google Scholar
Finney, M. A., Cohen, J. D., McAllister, S. S. & Jolly, W. M. 2012 On the need for a theory of wildland fire spread. Intl J. Wildland Fire 22, 25–36.Google Scholar
Floryan, D. & Floryan, J. M. 2015 Drag reduction in heated channels. J. Fluid Mech. 765, 353–395.CrossRefGoogle Scholar
Freund, G., Pesch, W. & Zimmermann, W. 2011 Rayleigh–Bénard convection in the presence of spatial temperature modulations. J. Fluid Mech. 673, 318–348.Google Scholar
Goluskin, D. & Doering, C. R. 2016 Bounds for convection between rough boundaries. J. Fluid. Mech. 804, 370–386.Google Scholar
Hassanzadeh, P., Chini, G. P. & Doering, C. R. 2014 Wall to wall optimal transport. J. Fluid Mech. 751, 627–662.CrossRefGoogle Scholar
Hossain, M. Z. & Floryan, J. M. 2013a Instabilities of natural convection in a periodically heated layer. J. Fluid Mech. 733, 33–67.Google Scholar
Hossain, M. Z. & Floryan, J. M. 2013b Heat transfer due to natural convection in a periodically heated slot. ASME J. Heat Transfer 135, 022503.Google Scholar
Hossain, M. Z. & Floryan, J. M. 2014 Natural convection in a fluid layer periodically heated from above. Phys. Rev. E 90, 023015.Google Scholar
Hossain, M. Z. & Floryan, J. M. 2015a Mixed convection in a periodically heated channel. J. Fluid Mech. 768, 51–90.CrossRefGoogle Scholar
Hossain, M. Z. & Floryan, J. M. 2015b Natural convection in a horizontal fluid layer periodically heated from above and below. Phys. Rev. E 92, 02301.Google Scholar
Hossain, M. Z. & Floryan, J. M. 2016 Drag reduction in a thermally modulated channel. J. Fluid Mech. 791, 122–153.Google Scholar
Hossain, M. Z. & Floryan, J. M. 2017 Natural convection under sub-critical conditions in the presence of heating non-uniformities. Intl J. Heat Mass Transfer 114, 8–19.Google Scholar
Hossain, M. Z., Floryan, D. & Floryan, J. M. 2012 Drag reduction due to spatial thermal modulations. J. Fluid Mech. 713, 398–419.Google Scholar
Hughes, G. O. & Griffiths, R. W. 2008 Horizontal convection. Annu. Rev. Fluid Mech. 40, 185–208.Google Scholar
Husain, S. Z. & Floryan, J. M. 2007 Immersed boundary conditions method for unsteady flow problems described by the Laplace operator. Intl J. Numer. Meth. Fluids 46, 1765–1786.Google Scholar
Husain, S. Z. & Floryan, J. M. 2010 Spectrally-accurate algorithm for moving boundary problems for the Navier–Stokes equations. J. Comput. Phys. 229, 2287–2313.CrossRefGoogle Scholar
Krishnan, M., Ugaz, V. M. & Burns, M. A. 2002 PCR in a Rayleigh–Bénard convection cell. Science 298, 793.Google Scholar
Lenardic, A., Moresi, L., Jellinek, A. M. & Manga, M. 2005 Continental insulation, mantle cooling, and the surface area of oceans and continents. Earth Planet. Sci. Lett. 234, 317–333.Google Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.Google Scholar
Marcq, S. & Weiss, J. 2012 Influence of sea ice lead-width distribution on turbulent heat transfer between the ocean and the atmosphere. Cryosphere 6, 143–156.Google Scholar
Maxworthy, T. 1997 Convection into domains with open boundaries. Annu. Rev. Fluid Mech. 29, 327–371.Google Scholar
McCoy, J. H., Brunner, W., Pesch, W. & Bodenschatz, E. 2008 Self-organization of topological defects due to applied constraints. Phys. Rev. Lett. 101, 254102.Google Scholar
Mohammadi, A. & Floryan, J. M. 2012 Mechanism of drag generation by surface corrugation. Phys. Fluids 24, 013602.Google Scholar
Rayleigh, J. W. S. 1916 On convection currents in a horizontal layer of fluid, when the higher temperature is on the under side. Phil. Mag. 32, 529–546.Google Scholar
Ripesi, P., Biferale, L., Sbragaglia, M. & Wirth, A. 2014 Natural convection with mixed insulating and conducting boundary conditions: low- and high-Rayleigh-number regimes. J. Fluid Mech. 742, 636–663.Google Scholar
Rizwam, A. M., Dennis, L. Y. C. & Liu, C. 2008 A review on the generation, determination and mitigation of urban heat island. J. Environ. Sci. 20, 120–128.Google Scholar
Seiden, G., Weiss, S., McCoy, J. H., Pesch, W. & Bodenschatz, E. 2008 Pattern forming system in the presence of different symmetry-breaking mechanisms. Phys. Rev. Lett. 101, 214503.Google Scholar
Siggers, J. H., Kerswell, R. R. & Balmforth, N. J. 2004 Bounds on horizontal convection. J. Fluid Mech. 517, 55–70.Google Scholar
Toppaladoddi, S., Succi, S. & Wettlaufer, J. S. 2015 Tailoring boundary geometry to optimize heat transport in turbulent convection. Eur. Phys. Lett. A 111, 44005.Google Scholar
Weiss, S., Seiden, G. & Bodenschatz, E. 2012 Pattern formation in spatially forced thermal convection. New J. Phys. 14, 053010.Google Scholar
Winters, K. B. & Young, W. R. 2009 Available potential energy and buoyancy variance in horizontal convection. J. Fluid Mech. 629, 221–230.Google Scholar