Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T16:43:06.557Z Has data issue: false hasContentIssue false
  • English
  • Français

Nanoparticle diffusion in sheared cellular blood flow

Published online by Cambridge University Press:  24 May 2019

Zixiang Liu Open the ORCID record for Zixiang Liu [Opens in a new window] ,
Jonathan R. Clausen ,
Rekha R. Rao  and
Cyrus K. Aidun Open the ORCID record for Cyrus K. Aidun [Opens in a new window]
Zixiang Liu
Affiliation:
George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA 30332, USA
Jonathan R. Clausen
Affiliation:
Sandia National Laboratories, Albuquerque, NM 87185, USA
Rekha R. Rao
Affiliation:
Sandia National Laboratories, Albuquerque, NM 87185, USA
Cyrus K. Aidun*
Affiliation:
George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA 30332, USA Parker H. Petit Institute for Bioengineering and Bioscience, Georgia Institute of Technology, Atlanta, GA 30332, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Using a multiscale blood flow solver, the complete diffusion tensor of nanoparticles (NPs) in sheared cellular blood flow is calculated over a wide range of shear rate and haematocrit. In the short-time regime, NPs exhibit anomalous dispersive behaviors under high shear and high haematocrit due to the transient elongation and alignment of the red blood cells (RBCs). In the long-time regime, the NP diffusion tensor features high anisotropy. Particularly, there exists a critical shear rate (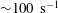${\sim}100~\text{s}^{-1}$) around which the shear-rate dependence of the diffusivity tensor changes from linear to nonlinear scale. Above the critical shear rate, the cross-stream diffusivity terms vary sublinearly with shear rate, while the longitudinal term varies superlinearly. The dependence on haematocrit is linear in general except at high shear rates, where a sublinear scale is found for the vorticity term and a quadratic scale for the longitudinal term. Through analysis of the suspension microstructure and numerical experiments, the nonlinear haemorheological dependence of the NP diffusion tensor is attributed to the streamwise elongation and cross-stream contraction of RBCs under high shear, quantified by a capillary number. The RBC size is shown to be the characteristic length scale affecting the RBC-enhanced shear-induced diffusion (RESID), while the NP submicrometre size exhibits negligible influence on the RESID. Based on the observed scaling behaviours, empirical correlations are proposed to bridge the NP diffusion tensor to specific shear rate and haematocrit. The characterized NP diffusion tensor provides a constitutive relation that can lead to more effective continuum models to tackle large-scale NP biotransport applications.

JFM classification

Biological Fluid Dynamics: Blood flow Multiphase and Particle-laden Flows: Particle/fluid flow Complex Fluids: Suspensions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 871 , 25 July 2019 , pp. 636 - 667
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlrichs, P. & Dünweg, B. 1998 Lattice-Boltzmann simulation of polymer–solvent systems. Intl J. Mod. Phys. C 09 (08), 1429–1438.10.1142/S0129183198001291Google Scholar
Ahlrichs, P. & Dünweg, B. 1999 Simulation of a single polymer chain in solution by combining lattice Boltzmann and molecular dynamics. J. Chem. Phys. 111 (17), 8225–8239.10.1063/1.480156Google Scholar
Ahmed, F., Mehrabadi, M., Liu, Z., Barabino, G. A. & Aidun, C. K. 2018 Internal viscosity-dependent margination of red blood cells in microfluidic channels. J. Biomech. Engng 140 (6), 061013.Google Scholar
Aidun, C. K. & Clausen, J. R. 2010 Lattice-Boltzmann method for complex flows. Annu. Rev. Fluid Mech. 42 (1), 439–472.10.1146/annurev-fluid-121108-145519Google Scholar
Aidun, C. K. & Lu, Y. 1995 Lattice Boltzmann simulation of solid particles suspended in fluid. J. Stat. Phys. 81 (1-2), 49–61.10.1007/BF02179967Google Scholar
Aidun, C. K., Lu, Y. N. & Ding, E. J. 1998 Direct analysis of particulate suspensions with inertia using the discrete Boltzmann equation. J. Fluid Mech. 373, 287–311.10.1017/S0022112098002493Google Scholar
Aidun, C. K. & Qi, D. W. 1998 A new method for analysis of the fluid interaction with a deformable membrane. J. Stat. Phys. 90 (1), 145–158.10.1023/A:1023299617476Google Scholar
Albanese, A., Tang, P. S. & Chan, W. C. 2012 The effect of nanoparticle size, shape, and surface chemistry on biological systems. Annu. Rev. Biomed. Engng 14, 1–16.Google Scholar
Antonini, G., Guiffant, G., Quemada, D. & Dosne, A. M. 1978 Estimation of platelet diffusivity in flowing blood. Biorheology 15 (2), 111–117.Google Scholar
Bhatnagar, P. L., Gross, E. P. & Krook, M. 1954 A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 94 (3), 511–525.Google Scholar
Blanco, E., Shen, H. & Ferrari, M. 2015 Principles of nanoparticle design for overcoming biological barriers to drug delivery. Nat. Biotechnol. 33 (9), 941–951.10.1038/nbt.3330Google Scholar
Brady, J. F. & Morris, J. F. 1997 Microstructure of strongly sheared suspensions and its impact on rheology and diffusion. J. Fluid Mech. 348, 103–139.10.1017/S0022112097006320Google Scholar
Breedveld, V., Van den Ende, D., Tripathi, A. & Acrivos, A. 1998 The measurement of the shear-induced particle and fluid tracer diffusivities in concentrated suspensions by a novel method. J. Fluid Mech. 375, 297–318.10.1017/S0022112098002808Google Scholar
Brook, R. D., Rajagopalan, S., Pope, C. A. 3rd, Brook, J. R., Bhatnagar, A., Diez-Roux, A. V., Holguin, F., Hong, Y., Luepker, R. V., Mittleman, M. A. et al. 2010 Particulate matter air pollution and cardiovascular disease: An update to the scientific statement from the american heart association. Circulation 121 (21), 2331–2378.Google Scholar
Bustamante, C., Bryant, Z. & Smith, S. B. 2003 Ten years of tension: single-molecule DNA mechanics. Nature 421 (6921), 423–427.10.1038/nature01405Google Scholar
Casa, L. D. C. & Ku, D. N. 2017 Thrombus formation at high shear rates. Annu. Rev. Biomed. Engng 19 (1), 415–433.10.1146/annurev-bioeng-071516-044539Google Scholar
Clausen, J. R. & Aidun, C. K. 2010 Capsule dynamics and rheology in shear flow: particle pressure and normal stress. Phys. Fluids 22 (12), 123302.Google Scholar
Clausen, J. R., Reasor, D. A. & Aidun, C. K. 2010 Parallel performance of a lattice-Boltzmann/finite element cellular blood flow solver on the IBM Blue Gene/p architecture. Comput. Phys. Commun. 181 (6), 1013–1020.Google Scholar
Clausen, J. R., Reasor, D. A. & Aidun, C. K. 2011 The rheology and microstructure of concentrated non-colloidal suspensions of deformable capsules. J. Fluid Mech. 685 (2011), 202–234.10.1017/jfm.2011.307Google Scholar
Da Cunha, F. R. & Hinch, E. J. 1996 Shear-induced dispersion in a dilute suspension of rough spheres. J. Fluid Mech. 309, 211–223.Google Scholar
Dao, M., Li, J. & Suresh, S. 2006 Molecularly based analysis of deformation of spectrin network and human erythrocyte. Mater. Sci. Engng C 26 (8), 1232–1244.10.1016/j.msec.2005.08.020Google Scholar
Decuzzi, P., Godin, B., Tanaka, T., Lee, S. Y., Chiappini, C., Liu, X. & Ferrari, M. 2010 Size and shape effects in the biodistribution of intravascularly injected particles. J. Control. Release 141 (3), 320–327.Google Scholar
Diller, T. E., Mikic, B. B. & Drinker, P. A. 1980 Shear-induced augmentation of oxygen transfer in blood. J. Biomech. Engng 102 (1), 67–72.Google Scholar
Ding, E. J. & Aidun, C. K. 2003 Extension of the lattice-Boltzmann method for direct simulation of suspended particles near contact. J. Stat. Phys. 112 (3–4), 685–708.10.1023/A:1023880126272Google Scholar
Eckstein, E. C. & Belgacem, F. 1991 Model of platelet transport in flowing blood with drift and diffusion terms. Biophys. J. 60 (1), 53–69.Google Scholar
Eckstein, E. C., Bailey, D. G. & Shapiro, A. H. 1977 Self-diffusion of particles in shear flow of a suspension. J. Fluid Mech. 79 (01), 191–208.Google Scholar
Fedosov, D. A., Caswell, B. & Karniadakis, G. E. 2010 A multiscale red blood cell model with accurate mechanics, rheology, and dynamics. Biophys. J. 98 (10), 2215–2225.10.1016/j.bpj.2010.02.002Google Scholar
Fedosov, D. A., Pan, W., Caswell, B., Gompper, G. & Karniadakis, G. E. 2011 Predicting human blood viscosity in silico. Proc. Natl Acad. Sci. USA 108 (29), 11772–11777.Google Scholar
Foss, D. R. & Brady, J. F. 1999 Self-diffusion in sheared suspensions by dynamic simulation. J. Fluid Mech. 401, 243–274.10.1017/S0022112099006576Google Scholar
Foss, D. R. & Brady, J. F. 2000a Brownian dynamics simulation of hard-sphere colloidal dispersions. J. Rheol. 44 (3), 629–651.10.1122/1.551104Google Scholar
Foss, D. R. & Brady, J. F. 2000b Structure, diffusion and rheology of Brownian suspensions by Stokesian dynamics simulation. J. Fluid Mech. 407, 167–200.10.1017/S0022112099007557Google Scholar
Grabowski, E. F., Friedman, L. I. & Leonard, E. F. 1972 Effects of shear rate on the diffusion and adhesion of blood platelets to a foreign surface. Ind. Engng Chem. Res. 11 (2), 224–232.Google Scholar
Griffin, M. T., Zhu, Y., Liu, Z., Aidun, C. K. & Ku, D. N. 2018 Inhibition of high shear arterial thrombosis by charged nanoparticles. Biomicrofluidics 12 (4), 042210.Google Scholar
Gross, M., Kruger, T. & Varnik, F. 2014 Fluctuations and diffusion in sheared athermal suspensions of deformable particles. Eur. Phys. Lett. 108 (6), 68006.10.1209/0295-5075/108/68006Google Scholar
Guo, Z., Zheng, C. & Shi, B. 2002 Discrete lattice effects on the forcing term in the lattice Boltzmann method. Phys. Rev. E 65 (4), 046308.Google Scholar
He, X., Zou, Q., Luo, L. S. & Dembo, M. 1997 Analytic solutions of simple flows and analysis of nonslip boundary conditions for the lattice Boltzmann BGK model. J. Stat. Phys. 87 (1–2), 115–136.10.1007/BF02181482Google Scholar
Hossain, S. S., Zhang, Y., Liang, X., Hussain, F., Ferrari, M., Hughes, T. J. & Decuzzi, P. 2013 In silico vascular modeling for personalized nanoparticle delivery. Nanomedicine 8 (3), 343–357.Google Scholar
Junk, M. & Yong, W.-A. 2003 Rigorous Navier–Stokes limit of the lattice Boltzmann equation. Asymp. Anal. 35, 165–185.Google Scholar
Kubo, R. 1966 The fluctuation–dissipation theorem. Rep. Prog. Phys. 29 (1), 255.Google Scholar
Kumar, A. & Graham, M. D. 2012 Mechanism of margination in confined flows of blood and other multicomponent suspensions. Phys. Rev. Lett. 109 (10), 108102.Google Scholar
Kumar, A. & Higdon, J. J. L. 2010 Origins of the anomalous stress behavior in charged colloidal suspensions under shear. Phys. Rev. E 82, 051401.Google Scholar
Kumar, A. & Higdon, J. J. L. 2011 Dynamics of the orientation behavior and its connection with rheology in sheared non-Brownian suspensions of anisotropic dicolloidal particles. J. Rheol. 55 (3), 581–626.Google Scholar
Lee, T. R., Choi, M., Kopacz, A. M., Yun, S. H., Liu, W. K. & Decuzzi, P. 2013 On the near-wall accumulation of injectable particles in the microcirculation: smaller is not better. Sci. Rep. 3, 2079.Google Scholar
Lees, A. W. & Edwards, S. F. 1972 The computer study of transport processes under extreme conditions. J. Phys. C 5 (15), 1921–1928.10.1088/0022-3719/5/15/006Google Scholar
Lipowsky, H. H. 2005 Microvascular rheology and hemodynamics. Microcirculation 12 (1), 5–15.Google Scholar
Liu, Y., Zhang, L., Wang, X. & Liu, W. K. 2004 Coupling of Navier–Stokes equations with protein molecular dynamics and its application to hemodynamics. Intl J. Numer. Meth. Fluids 46 (12), 1237–1252.10.1002/fld.798Google Scholar
Liu, Z., Zhu, Y., Rao, R. R., Clausen, J. R. & Aidun, C. K. 2018 Nanoparticle transport in cellular blood flow. Comput. Fluids 172, 609–620.Google Scholar
Liu, Z., Zhu, Y., Lechman, J. B., Rao, R. R., Clausen, J. R. & Aidun, C. K.2019 Multiscale method based on coupled lattice-Boltzmann and Langevin-dynamics for direct simulation of nanoscale particle/polymer suspensions in complex flows. Intl J. Numer. Meth. Fluids (in press).Google Scholar
MacMeccan, R. M., Clausen, J. R., Neitzel, G. P. & Aidun, C. K. 2009 Simulating deformable particle suspensions using a coupled lattice-Boltzmann and finite-element method. J. Fluid Mech. 618, 13–39.Google Scholar
Malysheva, A., Lombi, E. & Voelcker, N. H. 2015 Bridging the divide between human and environmental nanotoxicology. Nat. Nanotechnol. 10 (10), 835–844.Google Scholar
Mehrabadi, M., Ku, D. N. & Aidun, C. K. 2015 A continuum model for platelet transport in flowing blood based on direct numerical simulations of cellular blood flow. Ann. Biomed. Engng 43 (6), 1410–1421.10.1007/s10439-014-1168-4Google Scholar
Mehrabadi, M., Ku, D. N. & Aidun, C. K. 2016 Effects of shear rate, confinement, and particle parameters on margination in blood flow. Phys. Rev. E 93 (2), 023109.Google Scholar
Miller, M. R., Raftis, J. B., Langrish, J. P., McLean, S. G., Samutrtai, P., Connell, S. P., Wilson, S., Vesey, A. T., Fokkens, P. H. B., Boere, A. J. F. et al. 2017 Inhaled nanoparticles accumulate at sites of vascular disease. ACS Nano 11 (5), 4542–4552.10.1021/acsnano.6b08551Google Scholar
Morris, J. F. & Brady, J. F. 1996 Self-diffusion in sheared suspensions. J. Fluid Mech. 312, 223–252.Google Scholar
Mountrakis, L., Lorenz, E. & Hoekstra, A. G. 2016 Scaling of shear-induced diffusion and clustering in a blood-like suspension. Eur. Phys. Lett. 114 (1), 14002.10.1209/0295-5075/114/14002Google Scholar
Muller, K., Fedosov, D. A. & Gompper, G. 2014 Margination of micro- and nano-particles in blood flow and its effect on drug delivery. Sci. Rep. 4, 4871.10.1038/srep04871Google Scholar
Mynam, M., Sunthar, P. & Ansumali, S. 2011 Efficient lattice Boltzmann algorithm for Brownian suspensions. Phil. Trans. R. Soc. Lond. A 369 (1944), 2237–2245.Google Scholar
Neu, B. & Meiselman, H. J. 2002 Depletion-mediated red blood cell aggregation in polymer solutions. Biophys. J. 83 (5), 2482–2490.Google Scholar
Newby, D. E., Mannucci, P. M., Tell, G. S., Baccarelli, A. A., Brook, R. D., Donaldson, K., Forastiere, F., Franchini, M., Franco, O. H., Graham, I. et al. 2015 Expert position paper on air pollution and cardiovascular disease. Eur. Heart J. 36 (2), 83–93b.Google Scholar
Pednekar, S., Chun, J. & Morris, J. F. 2018 Bidisperse and polydisperse suspension rheology at large solid fraction. J. Rheol. 62 (2), 513–526.10.1122/1.5011353Google Scholar
Peskin, C. S. 2002 The immersed boundary method. Acta Numerica 11, 479–517.Google Scholar
Pivkin, I. V. & Karniadakis, G. E. 2008 Accurate coarse-grained modeling of red blood cells. Phys. Rev. Lett. 101 (11), 118105.10.1103/PhysRevLett.101.118105Google Scholar
Popel, A. S. & Johnson, P. C. 2005 Microcirculation and hemorheology. Annu. Rev. Fluid Mech. 37, 43–69.Google Scholar
Reasor, D. A., Clausen, J. R. & Aidun, C. K. 2012 Coupling the lattice-Boltzmann and spectrin-link methods for the direct numerical simulation of cellular blood flow. Intl J. Numer. Meth. Fluids 68 (6), 767–781.10.1002/fld.2534Google Scholar
Reasor, D. A., Clausen, J. R. & Aidun, C. K. 2013a Rheological characterization of cellular blood in shear. J. Fluid Mech. 726, 497–516.Google Scholar
Reasor, D. A. Jr, Mehrabadi, M., Ku, D. N. & Aidun, C. K. 2013b Determination of critical parameters in platelet margination. Ann. Biomed. Engng 41 (2), 238–249.Google Scholar
Shang, L., Nienhaus, K. & Nienhaus, G. U. 2014 Engineered nanoparticles interacting with cells: size matters. J. Nanobiotechnol. 12 (1), 5.Google Scholar
Siegle, P., Goychuk, I. & Hanggi, P. 2010 Origin of hyperdiffusion in generalized Brownian motion. Phys. Rev. Lett. 105 (10), 100602.Google Scholar
Sierou, A. & Brady, J. F. 2004 Shear-induced self-diffusion in non-colloidal suspensions. J. Fluid Mech. 506 (506), 285–314.Google Scholar
Wagner, A. J. & Pagonabarraga, I. 2002 Lees–Edwards boundary conditions for lattice Boltzmann. J. Stat. Phys. 107 (1/2), 521–537.Google Scholar
Wang, M. & Brady, J. F. 2016 Spectral Ewald acceleration of Stokesian dynamics for polydisperse suspensions. Comput. Phys. 306, 443–477.Google Scholar
Wang, N. H. L. & Keller, K. H. 1985 Augmented transport of extracellular solutes in concentrated erythrocyte suspensions in Couette-flow. J. Colloid Interf. Sci. 103 (1), 210–225.Google Scholar
Wu, J. & Aidun, C. K. 2010 Simulating 3D deformable particle suspensions using lattice Boltzmann method with discrete external boundary force. Intl J. Numer. Meth. Fluids 62 (7), 765–783.Google Scholar
Xue, W. & Grest, G. S. 1990 Shear-induced alignment of colloidal particles in the presence of a shear flow. Phys. Rev. Lett. 64 (4), 419–422.Google Scholar
Yeo, K. & Maxey, M. R. 2010 Anomalous diffusion of wall-bounded non-colloidal suspensions in a steady shear flow. Eur. Phys. Lett. 92 (2), 24008.Google Scholar
Yoo, J. W., Irvine, D. J., Discher, D. E. & Mitragotri, S. 2011 Bio-inspired, bioengineered and biomimetic drug delivery carriers. Nat. Rev. Drug Discov. 10 (7), 521–535.Google Scholar
Zhao, H. & Shaqfeh, E. S. G. 2011 Shear-induced platelet margination in a microchannel. Phys. Rev. E 83, 061924.Google Scholar
Zhao, H., Shaqfeh, E. S. G. & Narsimhan, V. 2012 Shear-induced particle migration and margination in a cellular suspension. Phys. Fluids 24 (1), 011902.Google Scholar
Zia, R. N. & Brady, J. F. 2010 Single-particle motion in colloids: force-induced diffusion. J. Fluid Mech. 658, 188–210.Google Scholar
Zydney, A. L. & Colton, C. K. 1988 Augmented solute transport in the shear flow of a concentrated suspension. Hydrodynamics 10 (1), 77–96.Google Scholar

Liu Supplementary Movie 1

Instantaneous NP-RBC distribution under unbounded simple shear flow at 100 s-1 shear rate and 40% RBC concentration. Views on the left column show all the NPs and RBCs. Views on the right column show only a few RBCs so as to visualize the NP phase and the single RBC morphology.

Download Liu Supplementary Movie 1(Video)
Video 10.4 MB

Liu Supplementary Movie 2

Instantaneous NP-RBC distribution under unbounded simple shear flow at 2000 s-1 shear rate and 40% RBC concentration. Views on the left column show all the NPs and RBCs. Views on the right column show only a few RBCs so as to visualize the NP phase and the single RBC morphology.

Download Liu Supplementary Movie 2(Video)
Video 10.6 MB