Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T09:07:05.410Z Has data issue: false hasContentIssue false
  • English
  • Français

Multi-species turbulent mixing under supercritical-pressure conditions: modelling, direct numerical simulation and analysis revealing species spinodal decomposition

Published online by Cambridge University Press:  19 March 2013

Enrica Masi ,
Josette Bellan ,
Kenneth G. Harstad  and
Nora A. Okong’o
Enrica Masi
Affiliation:
California Institute of Technology, Pasadena, CA 91125, USA
Josette Bellan*
Affiliation:
California Institute of Technology, Pasadena, CA 91125, USA Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA 91109, USA
Kenneth G. Harstad
Affiliation:
Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA 91109, USA
Nora A. Okong’o
Affiliation:
Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA 91109, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A model is developed for describing mixing of several species under high-pressure conditions. The model includes the Peng–Robinson equation of state, a full mass-diffusion matrix, a full thermal-diffusion-factor matrix necessary to incorporate the Soret and Dufour effects and both thermal conductivity and viscosity computed for the species mixture using mixing rules. Direct numerical simulations (DNSs) are conducted in a temporal mixing layer configuration. The initial mean flow is perturbed using an analytical perturbation which is consistent with the definition of vorticity and is divergence free. Simulations are performed for a set of five species relevant to hydrocarbon combustion and an ensemble of realizations is created to explore the effect of the initial Reynolds number and of the initial pressure. Each simulation reaches a transitional state having turbulent characteristics and most of the data analysis is performed on that state. A mathematical reformulation of the flux terms in the conservation equations allows the definition of effective species-specific Schmidt numbers 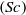$(\mathit{Sc})$ and of an effective Prandtl number 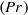$(\mathit{Pr})$ based on effective species-specific diffusivities and an effective thermal conductivity, respectively. Because these effective species-specific diffusivities and the effective thermal conductivity are not directly computable from the DNS solution, we develop models for both of these quantities that prove very accurate when compared with the DNS database. For two of the five species, values of the effective species-specific diffusivities are negative at some locations indicating that these species experience spinodal decomposition; we determine the necessary and sufficient condition for spinodal decomposition to occur. We also show that flows displaying spinodal decomposition have enhanced vortical characteristics and trace this aspect to the specific features of high-density-gradient magnitude regions formed in the flows. The largest values of the effective species-specific 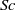$\mathit{Sc}$ numbers can be well in excess of those known for gases but almost two orders of magnitude smaller than those of liquids at atmospheric pressure. The effective thermal conductivity also exhibits negative values at some locations and the effective 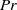$\mathit{Pr}$ displays values that can be as high as those of a liquid refrigerant. Examination of the equivalence ratio indicates that the stoichiometric region is thin and coincides with regions where the mixture effective species-specific Lewis number values are well in excess of unity. Very lean and very rich regions coexist in the vicinity of the stoichiometric region. Analysis of the dissipation indicates that it is dominated by mass diffusion, with viscous dissipation being the smallest among the three dissipation modes. The sum of the heat and species (i.e. scalar) dissipation is functionally modelled using the effective species-specific diffusivities and the effective thermal conductivity. Computations of the modelled sum employing the modelled effective species-specific diffusivities and the modelled effective thermal conductivity shows that it accurately replicates the exact equivalent dissipation.

JFM classification

Mixing: Mixing Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 721 , 25 April 2013 , pp. 578 - 626
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balluffi, R. W., Allen, S. M. & Carter, W. C. 2005 Kinetics of Materials. John Wiley & Sons.CrossRefGoogle Scholar
Batchelor, G. K. 1999 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Bellan, J. 2006 Theory, modelling and analysis of turbulent supercritical mixing. Combust. Sci. Technol. 178, 253–281.CrossRefGoogle Scholar
Cahn, J. W. & Hilliard, J. E. 1958 Free energy of a non-uniform system. I. Interfacial free energy. J. Chem. Phys. 28 (2), 258–267.CrossRefGoogle Scholar
de Groot, S. R. & Mazur, P. 1984 Non-equilibrium Thermodynamics. Dover.Google Scholar
Egolfopoulos, F. N. & Dimotakis, P. E. 1998 Non-premixed hydrocarbon ignition at high strain rates. Proc. Combust. Inst. 27, 641–648.Google Scholar
Ern, A. & Giovangigli, V. 1994 Multicomponent transport algorithms. In Lecture Notes in Physics Monographs, M 24. Springer.Google Scholar
Ern, A. & Giovangigli, V. 1998 Thermal diffusion effects in hydrogen–air and methane–air flames. Combust. Theor. Model. 2, 349–372.CrossRefGoogle Scholar
Fotache, C. G., Kreutz, T. G. & Law, C. K. 1997 Ignition of counterflowing methane versus heated air under reduced and elevated pressures. Combust. Flame 108, 442–470.CrossRefGoogle Scholar
Giovangigli, V. 1991 Convergent iterative methods for multicomponent diffusion. Impact Comput. Sci. Engng 3, 244–276.Google Scholar
Giovangigli, V., Matuszewsky, L. & Dupoirieux, F. 2011 Detailed modelling of planar transcritical ${\text{H} }_{2} \text{{\ndash}} {\text{O} }_{2} \text{{\ndash}} {\text{N} }_{2} $ flames. Combust. Theor. Model. 15, 141–182.Google Scholar
Giovangigli, V. & Matuszewsky, L. 2012 Numerical simulation of transcritical strained laminar flames. Combust. Flame 159, 2829–2840.CrossRefGoogle Scholar
Goto, S. & Kida, S. 1999 Passive scalar spectrum in isotropic turbulence: prediction by the Lagrangian direct-interaction approximation. Phys. Fluids 11 (7), 1936–1952.CrossRefGoogle Scholar
Hannoun, I. A., Fernando, H. J. S. & List, E. J. 1988 Turbulence structure near a sharp density interface. J. Fluid Mech. 189, 189–209.CrossRefGoogle Scholar
Harstad, K. & Bellan, J. 1999 The Lewis number under supercritical conditions. Intl J. Heat Mass Transfer 42, 961–970.Google Scholar
Harstad, K. & Bellan, J. 2004a Mixing rules for multicomponent mixture mass diffusion coefficients and thermal diffusion factors. J. Chem. Phys. 120 (12), 5664–5673.Google Scholar
Harstad, K. & Bellan, J. 2004b High-pressure binary mass-diffusion coefficients for combustion applications. Ind. Engng Chem. Res. 43 (2), 645–654.CrossRefGoogle Scholar
Hirshfelder, J. & Curtis, C. 1949 Theory of propagation of flames. Part I. General equations. In Third Symposium (International) on Combustion, pp. 121–127. The Williams & Wilkins Co.Google Scholar
Hirshfelder, J., Curtis, C. & Bird, R. 1964 Molecular Theory of Gases and Liquids. John Wiley and Sons.Google Scholar
Keizer, J. 1987 Statistical Thermodynamics of Nonequilibrium Processes. Springler.CrossRefGoogle Scholar
Kennedy, C. & Carpenter, M. 1994 Several new numerical methods for compressible shear layer simulations. Appl. Numer. Maths 14, 397–433.CrossRefGoogle Scholar
Moser, R. & Rogers, M. 1991 Mixing transition and the cascade to small scales in a plane mixing layer. Phys. Fluids A 3 (5), 1128–1134.CrossRefGoogle Scholar
Muller, S. M. & Scheerer, D. 1991 A method to parallelize tridiagonal solvers. Parallel Comput. 17, 181–188.Google Scholar
Nauman, E. B & He, D. Q. 2001 Nonlinear diffusion and phase separation. Chem. Engng Sci. 56, 1999–2018.Google Scholar
Okong’o, N. & Bellan, J. 2002a Direct numerical simulation of a transitional supercritical binary mixing layer: heptane and nitrogen. J. Fluid Mech. 464, 1–34.CrossRefGoogle Scholar
Okong’o, N., Harstad, K. & Bellan, J. 2002 Direct numerical simulations of ${\mathrm{O} }_{2} / {\mathrm{H} }_{2} $ temporal mixing layers under supercritical conditions. AIAA J. 40 (5), 914–926.CrossRefGoogle Scholar
Okong’o, N. & Bellan, J. 2002b Consistent boundary conditions for multicomponent real gas mixtures based on characteristic waves. J. Comput. Phys. 176, 330–344.CrossRefGoogle Scholar
Okong’o, N. & Bellan, J. 2004 Perturbation and initial Reynolds number effects on transition attainment of supercritical mixing layers. Comput. Fluids 33 (8), 1023–1046.CrossRefGoogle Scholar
Papamoschou, D. & Roshko, A. 1988 The compressible turbulent shear layer: an experimental study. J. Fluid Mech. 197, 453–477.Google Scholar
Peters, N. 2000 Turbulent Combustion. Cambridge University Press.Google Scholar
Pine, D. J., Easwar, N., Maher, J. V. & Goldburg, W. I. 1984 Turbulent suppression of spinodal decomposition. Phys. Rev. A. 29 (1), 308–313.CrossRefGoogle Scholar
Pitsch, H. & Peters, N. 1998 Investigation of the ignition process of sprays under diesel engine conditions using n-heptane chemistry. SAE paper 98-2464.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Rehfeldt, S. & Stichlmair, J. 2007 Measurement and calculation of multicomponent diffusion coefficients in liquids. Fluid Phase Equilib. 256, 99–104.CrossRefGoogle Scholar
Rehfeldt, S. & Stichlmair, J. 2010 Measurement and prediction of multicomponent diffusion coefficients in four ternary liquid systems. Fluid Phase Equilib. 290, 1–14.Google Scholar
Reid, R. C., Prausnitz, J. M. & Polling, B. E. 1987 The Properties of Gases and Liquids, 4th edn. McGraw-Hill.Google Scholar
Selle, L. C., Okong’o, N. A., Bellan, J. & Harstad, K. G. 2007 Modelling of subgrid scale phenomena in supercritical transitional mixing layers: an a priori study. J. Fluid Mech. 593, 57–91.Google Scholar
Tennekes, H. & Lumley, J. L. 1989 A First Course in Turbulence. MIT.Google Scholar
Williams, F A. 1975 Turbulent mixing in non-reactive and reactive flows. In Recent Advances in the Theoretical Descriptions of Turbulent Diffusion Flames (ed. Murthy, S.). pp. 189–208. Plenum.Google Scholar