Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Yuan, Quanzi
and
Zhao, Ya-Pu
2013.
Wetting on flexible hydrophilic pillar-arrays.
Scientific Reports,
Vol. 3,
Issue. 1,
Pandey, Prithvi Raj
and
Roy, Sudip
2013.
Is it Possible to Change Wettability of Hydrophilic Surface by Changing Its Roughness?.
The Journal of Physical Chemistry Letters,
Vol. 4,
Issue. 21,
p.
3692.
Li Chun-Xi
Pei Jian-Jun
and
Ye Xue-Min
2013.
Dynamics of insoluble surfactant-laden thin films flow over inclined random topography.
Acta Physica Sinica,
Vol. 62,
Issue. 21,
p.
214704.
Li Chun-Xi
Pei Jian-Jun
and
Ye Xue-Min
2013.
Stability of liquid droplet containing insoluble surfactant spreading over corrugated topography.
Acta Physica Sinica,
Vol. 62,
Issue. 17,
p.
174702.
Zhu, Jianzhong
Zangari, Giovanni
and
Reed, Michael L.
2013.
Three-phase contact force equilibrium of liquid drops at hydrophilic and superhydrophobic surfaces.
Journal of Colloid and Interface Science,
Vol. 404,
Issue. ,
p.
179.
Chen, Longquan
and
Bonaccurso, Elmar
2014.
Effects of surface wettability and liquid viscosity on the dynamic wetting of individual drops.
Physical Review E,
Vol. 90,
Issue. 2,
Zhao, Yapu
2014.
Moving contact line problem: Advances and perspectives.
Theoretical and Applied Mechanics Letters,
Vol. 4,
Issue. 3,
p.
034002.
Hao, PengFei
Lv, CunJing
Yao, ZhaoHui
and
Niu, FengLei
2014.
Wetting property of smooth and textured hydrophobic surfaces under condensation condition.
Science China Physics, Mechanics & Astronomy,
Vol. 57,
Issue. 11,
p.
2127.
Wang, LiYa
Wang, FengChao
Yang, FuQian
and
Wu, HengAn
2014.
Molecular kinetic theory of boundary slip on textured surfaces by molecular dynamics simulations.
Science China Physics, Mechanics & Astronomy,
Vol. 57,
Issue. 11,
p.
2152.
Yuan, Quanzi
Huang, Xianfu
and
Zhao, Ya-Pu
2014.
Dynamic spreading on pillar-arrayed surfaces: Viscous resistance versus molecular friction.
Physics of Fluids,
Vol. 26,
Issue. 9,
Sun, Chang Q.
2014.
Relaxation of the Chemical Bond.
Vol. 108,
Issue. ,
p.
775.
Li, Chunxi
Pei, Jianjun
and
Ye, Xuemin
2014.
Spreading of droplet with insoluble surfactant on corrugated topography.
Physics of Fluids,
Vol. 26,
Issue. 9,
Chamakos, Nikolaos T.
Kavousanakis, Michail E.
and
Papathanasiou, Athanasios G.
2014.
Neither Lippmann nor Young: Enabling Electrowetting Modeling on Structured Dielectric Surfaces.
Langmuir,
Vol. 30,
Issue. 16,
p.
4662.
Sun, Quanmei
Ao, Zhuo
Feng, Jiantao
Li, Hongyi
and
Han, Dong
2014.
Micro/-nanoscaled topography-coupled-mechanical action into functional biointerface.
Chinese Science Bulletin,
Vol. 59,
Issue. 28,
p.
3523.
Kavousanakis, Michail E.
Chamakos, Nikolaos T.
and
Papathanasiou, Athanasios G.
2015.
Connection of Intrinsic Wettability and Surface Topography with the Apparent Wetting Behavior and Adhesion Properties.
The Journal of Physical Chemistry C,
Vol. 119,
Issue. 27,
p.
15056.
Huang, Yongli
Zhang, Xi
Ma, Zengsheng
Zhou, Yichun
Zheng, Weitao
Zhou, Ji
and
Sun, Chang Q.
2015.
Hydrogen-bond relaxation dynamics: Resolving mysteries of water ice.
Coordination Chemistry Reviews,
Vol. 285,
Issue. ,
p.
109.
Yuan, Zeshuai
Lu, Zixing
Chen, Mingyang
Yang, Zhenyu
and
Xie, Fan
2015.
Interfacial properties of carboxylic acid functionalized CNT/polyethylene composites: A molecular dynamics simulation study.
Applied Surface Science,
Vol. 351,
Issue. ,
p.
1043.
Raees, A.
Xu, Hang
Sun, Qiang
and
Pop, I.
2015.
Mixed convection in gravity-driven nano-liquid film containing both nanoparticles and gyrotactic microorganisms.
Applied Mathematics and Mechanics,
Vol. 36,
Issue. 2,
p.
163.
Li, Yanru
Tang, Chao
Zhong, Jianxin
and
Meng, Lijun
2015.
Dewetting and detachment of Pt nanofilms on graphitic substrates: A molecular dynamics study.
Journal of Applied Physics,
Vol. 117,
Issue. 6,
Li, YingQi
Wang, FengChao
Liu, He
and
Wu, HengAn
2015.
Nanoparticle-tuned spreading behavior of nanofluid droplets on the solid substrate.
Microfluidics and Nanofluidics,
Vol. 18,
Issue. 1,
p.
111.
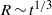 $R\sim {t}^{1/ 3} $ for the rough surface and
$R\sim {t}^{1/ 3} $ for the rough surface and 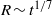 $R\sim {t}^{1/ 7} $ for the smooth surface. The scaling laws were validated by both the experiments and the simulations. Our results may help in understanding the dynamic wetting of a droplet on a pillar-arrayed lyophilic substrate and assisting the future design of pillar-arrayed lyophilic surfaces in practical applications.
$R\sim {t}^{1/ 7} $ for the smooth surface. The scaling laws were validated by both the experiments and the simulations. Our results may help in understanding the dynamic wetting of a droplet on a pillar-arrayed lyophilic substrate and assisting the future design of pillar-arrayed lyophilic surfaces in practical applications.