Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-19T18:54:05.409Z Has data issue: false hasContentIssue false
  • English
  • Français

Moving contact line dynamics: from diffuse to sharp interfaces

Published online by Cambridge University Press:  22 December 2015

H. Kusumaatmaja ,
E. J. Hemingway  and
S. M. Fielding
H. Kusumaatmaja*
Affiliation:
Department of Physics, Durham University, South Road, Durham DH1 3LE, UK
E. J. Hemingway
Affiliation:
Department of Physics, Durham University, South Road, Durham DH1 3LE, UK
S. M. Fielding
Affiliation:
Department of Physics, Durham University, South Road, Durham DH1 3LE, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

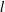We reconcile two scaling laws that have been proposed in the literature for the slip length associated with a moving contact line in diffuse interface models, by demonstrating each to apply in a different regime of the ratio of the microscopic interfacial width $l$ and the macroscopic diffusive length 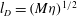$l_{D}=(M{\it\eta})^{1/2}$, where 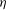${\it\eta}$ is the fluid viscosity and 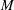$M$ the mobility governing intermolecular diffusion. For small 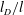$l_{D}/l$ we find a diffuse interface regime in which the slip length scales as 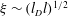${\it\xi}\sim (l_{D}l)^{1/2}$. For larger 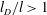$l_{D}/l>1$ we find a sharp interface regime in which the slip length depends only on the diffusive length, 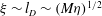${\it\xi}\sim l_{D}\sim (M{\it\eta})^{1/2}$, and therefore only on the macroscopic variables 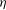${\it\eta}$ and 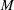$M$, independent of the microscopic interfacial width 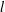$l$. We also give evidence that modifying the microscopic interfacial terms in the model’s free energy functional appears to affect the value of the slip length only in the diffuse interface regime, consistent with the slip length depending only on macroscopic variables in the sharp interface regime. Finally, we demonstrate the dependence of the dynamic contact angle on the capillary number to be in excellent agreement with the theoretical prediction of Cox (J. Fluid Mech., vol. 168, 1986, p. 169), provided we allow the slip length to be rescaled by a dimensionless prefactor. This prefactor appears to converge to unity in the sharp interface limit, but is smaller in the diffuse interface limit. The excellent agreement of results obtained using three independent numerical methods, across several decades of the relevant dimensionless variables, demonstrates our findings to be free of numerical artefacts.

JFM classification

Interfacial Flows (free surface): Contact lines Interfacial Flows (free surface): Interfacial Flows (free surface) Multiphase and Particle-laden Flows: Multiphase flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 788 , 10 February 2016 , pp. 209 - 227
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aarts, D. G. A. L., Dullens, R. P. A., Lekkerkerker, H. N. W., Bonn, D. & van Roij, R. 2004 Interfacial tension and wetting in colloid–polymer mixtures. J. Chem. Phys. 120, 1973–1980.CrossRefGoogle ScholarPubMed
Anderson, D. M., McFadden, G. B. & Wheeler, A. A. 1998 Diffuse-interface methods in fluid mechanics. Annu. Rev. Fluid Mech. 30, 139–165.CrossRefGoogle Scholar
Bray, A. J. 1994 Theory of phase-ordering kinetics. Adv. Phys. 43, 357–459.CrossRefGoogle Scholar
Briant, A. J., Wagner, A. J. & Yeomans, J. M. 2004 Lattice Boltzmann simulations of contact line motion. I. Liquid–gas systems. Phys. Rev. E 69, 031602.Google Scholar
Briant, A. J. & Yeomans, J. M. 2004 Lattice Boltzmann simulations of contact line motion. II. Binary fluids. Phys. Rev. E 69, 031603.Google Scholar
Cahn, J. W. 1977 Critical point wetting. J. Chem. Phys. 66, 3667–3672.Google Scholar
Chen, H.-Y., Jasnow, D. & Viñals, J. 2000 Interface and contact line motion in a two phase fluid under shear flow. Phys. Rev. Lett. 85, 1686–1689.CrossRefGoogle Scholar
Cox, R. G. 1986 The dynamics of the spreading of liquids on a solid surface. Part 1. Viscous flow. J. Fluid Mech. 168, 169.CrossRefGoogle Scholar
Davidovitch, B., Moro, E. & Stone, H. A. 2005 Spreading of viscous fluid drops on a solid substrate assisted by thermal fluctuations. Phys. Rev. Lett. 95, 244505.Google Scholar
Diotallevi, F., Biferale, L., Chibbaro, S., Pontrelli, G., Toschi, F. & Succi, S. 2009 Lattice Boltzmann simulations of capillary filling: finite vapour density effects. Eur. Phys. J. Spec. Top. 171, 237–243.Google Scholar
Eggers, J. 2004 Hydrodynamic theory of forced dewetting. Phys. Rev. Lett. 93, 094502.CrossRefGoogle ScholarPubMed
Eyre, D. J.1998 An unconditionally stable one-step scheme for gradient systems. http://www.math.utah.edu/∼eyre/research/methods/stable.ps, pp. 1–15.Google Scholar
de Gennes, P. G. 1985 Wetting: statics and dynamics. Rev. Mod. Phys. 57, 827–863.CrossRefGoogle Scholar
Gompper, G. & Zschocke, S. 1991 Elastic properties of interfaces in a Ginzburg–Landau theory of swollen micelles, droplet crystals and lamellar phases. Europhys. Lett. 16, 731–736.Google Scholar
Gross, M. & Varnik, F. 2014 Spreading dynamics of nanodrops: a lattice Boltzmann study. Intl J. Mod. Phys. C 25, 1340019.Google Scholar
Guillén-González, F. & Tierra, G. 2013 On linear schemes for a Cahn–Hilliard diffuse interface model. J. Comput. Phys. 234, 140–171.CrossRefGoogle Scholar
Hu, D. L., Chan, B. & Bush, J. W. M. 2003 The hydrodynamics of water strider locomotion. Nature 424, 663–666.CrossRefGoogle ScholarPubMed
Huh, C. & Scriven, L. E. 1971 Hydrodynamic model of steady movement of a solid/liquid/fluid contact line. J. Colloid Interface Sci. 35, 85–101.Google Scholar
Jacqmin, D. 1999 Calculation of two-phase Navier–Stokes flows using phase-field modeling. J. Comput. Phys. 155, 96–127.CrossRefGoogle Scholar
Jacqmin, D. 2000 Contact-line dynamics of a diffuse fluid interface. J. Fluid Mech. 402, 57–88.Google Scholar
Ladd, A. J. C. & Verberg, R. 2001 Lattice–Boltzmann simulations of particle–fluid suspensions. J. Stat. Phys. 104, 1191–1251.Google Scholar
Lai, M.-C. & Peskin, C. S. 2000 An immersed boundary method with formal second-order accuracy and reduced numerical viscosity. J. Comput. Phys. 160, 705–719.CrossRefGoogle Scholar
Lu, C.-Y. D., Olmsted, P. D. & Ball, R. C. 2000 Effects of nonlocal stress on the determination of shear banding flow. Phys. Rev. Lett. 84, 642–645.Google Scholar
Mognetti, B. M., Kusumaatmaja, H. & Yeomans, J. M. 2010 Drop dynamics on hydrophobic and superhydrophobic surfaces. Faraday Discuss. 146, 153–165.Google Scholar
Morrow, N. R. 1990 Wettability and its effect on oil recovery. J. Petrol. Tech. 42, 1476–1484.Google Scholar
Olmsted, P. D. & Lu, C.-Y. D. 1999 Phase coexistence of complex fluids in shear flow. Faraday Discuss. 112, 183–194.Google Scholar
Parker, A. R. & Lawrence, C. R. 2001 Water capture by a desert beetle. Nature 414, 33–34.Google Scholar
Peskin, C. S. 2002 The immersed boundary method. Acta Numerica 11, 479–517.Google Scholar
Pooley, C. M., Kusumaatmaja, H. & Yeomans, J. M. 2008 Contact line dynamics in binary lattice Boltzmann simulations. Phys. Rev. E 78, 056709.Google Scholar
Pooley, C. M., Kusumaatmaja, H. & Yeomans, J. M. 2009 Modelling capillary filling dynamics using lattice Boltzmann simulations. Eur. Phys. J. Spec. Top. 171, 63–71.Google Scholar
Pozrikidis, C. 2011 Introduction to Theoretical and Computational Fluid Dynamics. Oxford University Press.Google Scholar
Press, W. H., Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. 1992 Numerical Recipes in C. Cambridge University Press.Google Scholar
Renardy, M., Renardy, Y. & Li, J. 2001 Numerical simulation of moving contact line problems using a volume-of-fluid method. J. Comput. Phys. 171, 243–263.Google Scholar
Sbragaglia, M., Sugiyama, K. & Biferale, L. 2008 Wetting failure and contact line dynamics in a couette flow. J. Fluid Mech. 614, 471–493.CrossRefGoogle Scholar
Seppecher, P. 1996 Moving contact lines in the Cahn–Hilliard theory. Intl J. Engng Sci. 34, 977–992.Google Scholar
Servantie, J. & Muller, M. 2008 Statics and dynamics of a cylindrical droplet under an external body force. J. Chem. Phys. 128, 014709.Google Scholar
Setu, S. A., Dullens, R. P. A., Hernndez-Machado, A., Pagonabarraga, I., Aarts, D. G. A. L. & Ledesma-Aguilar, R. 2015 Superconfinement tailors fluid flow at microscales. Nature Commun. 6, 7297.Google Scholar
Spelt, P. D.M. 2005 A level-set approach for simulations of flows with multiple moving contact lines with hysteresis. J. Comput. Phys. 207, 389–404.Google Scholar
Tabeling, P. 2010 Introduction to Microfluidics. Oxford University Press.Google Scholar
Thampi, S. P., Adhikari, R. & Govindarajan, R. 2013 Do liquid drops roll or slide on inclined surfaces? Langmuir 29, 3339–3346.Google Scholar
Yue, P., Zhou, C. & Feng, J. J. 2010 Sharp-interface limit of the Cahn–Hilliard model for moving contact lines. J. Fluid Mech. 645, 279.Google Scholar
Zheng, Y., Gao, X. & Jiang, L. 2007 Directional adhesion of superhydrophobic butterfly wings. Soft Matt. 3, 178–182.Google Scholar
Zhou, M.-Y. & Sheng, P. 1990 Dynamics of immiscible-fluid displacement in a capillary tube. Phys. Rev. Lett. 64, 882–885.Google Scholar