Article contents
Moment generating functions and scaling laws in the inertial layer of turbulent wall-bounded flows
Published online by Cambridge University Press: 16 February 2016
Abstract
Properties of single- and two-point moment generating functions (MGFs) are examined in the inertial region of wall-bounded flows. Empirical evidence for power-law scaling of the single-point MGF 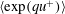 $\langle \text{exp}(qu^{+})\rangle$ (where
$\langle \text{exp}(qu^{+})\rangle$ (where 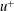 $u^{+}$ is the normalized streamwise velocity fluctuation and
$u^{+}$ is the normalized streamwise velocity fluctuation and 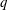 $q$ a real parameter) with respect to the wall-normal distance is presented, based on hot-wire data from a
$q$ a real parameter) with respect to the wall-normal distance is presented, based on hot-wire data from a 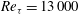 $Re_{{\it\tau}}=13\,000$ boundary-layer experiment. The parameter
$Re_{{\it\tau}}=13\,000$ boundary-layer experiment. The parameter 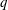 $q$ serves as a ‘dial’ to emphasize different parts of the signal such as high- and low-speed regions, for positive and negative values of
$q$ serves as a ‘dial’ to emphasize different parts of the signal such as high- and low-speed regions, for positive and negative values of 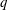 $q$, respectively. Power-law scaling
$q$, respectively. Power-law scaling  $\langle \text{exp}(qu^{+})\rangle \sim (z/{\it\delta})^{-{\it\tau}(q)}$ can be related to the generalized logarithmic laws previously observed in higher-order moments, such as in
$\langle \text{exp}(qu^{+})\rangle \sim (z/{\it\delta})^{-{\it\tau}(q)}$ can be related to the generalized logarithmic laws previously observed in higher-order moments, such as in 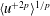 $\langle u^{+2p}\rangle ^{1/p}$, but provide additional information not available through traditional moments if considering
$\langle u^{+2p}\rangle ^{1/p}$, but provide additional information not available through traditional moments if considering 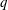 $q$ values away from the origin. For two-point MGFs, the scalings in
$q$ values away from the origin. For two-point MGFs, the scalings in 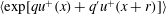 $\langle \text{exp}[qu^{+}(x)+q^{\prime }u^{+}(x+r)]\rangle$ with respect to
$\langle \text{exp}[qu^{+}(x)+q^{\prime }u^{+}(x+r)]\rangle$ with respect to  $z$ and streamwise displacement
$z$ and streamwise displacement  $r$ in the logarithmic region are investigated. The special case
$r$ in the logarithmic region are investigated. The special case  $q^{\prime }=-q$ is of particular interest, since this choice emphasizes rare events with high and low speeds at a distance
$q^{\prime }=-q$ is of particular interest, since this choice emphasizes rare events with high and low speeds at a distance  $r$. Applying simple scaling arguments motivated by the attached eddy model, a ‘scaling transition’ is predicted to occur for
$r$. Applying simple scaling arguments motivated by the attached eddy model, a ‘scaling transition’ is predicted to occur for 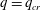 $q=q_{cr}$ such that
$q=q_{cr}$ such that 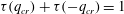 ${\it\tau}(q_{cr})+{\it\tau}(-q_{cr})=1$, where
${\it\tau}(q_{cr})+{\it\tau}(-q_{cr})=1$, where 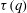 ${\it\tau}(q)$ is the set of scaling exponents for single-point MGFs. This scaling transition is not visible to traditional central moments, but is indeed observed based on the experimental data, illustrating the capabilities of MGFs to provide new and statistically robust insights into turbulence structure and confirming essential ingredients of the attached eddy model.
${\it\tau}(q)$ is the set of scaling exponents for single-point MGFs. This scaling transition is not visible to traditional central moments, but is indeed observed based on the experimental data, illustrating the capabilities of MGFs to provide new and statistically robust insights into turbulence structure and confirming essential ingredients of the attached eddy model.
JFM classification
- Type
- Rapids
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 38
- Cited by



