Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-08T16:34:55.793Z Has data issue: false hasContentIssue false
  • English
  • Français

Modes of synchronisation in the wake of a streamwise oscillatory cylinder

Published online by Cambridge University Press:  26 October 2017

Guoqiang Tang ,
Liang Cheng ,
Feifei Tong Open the ORCID record for Feifei Tong [Opens in a new window] ,
Lin Lu  and
Ming Zhao Open the ORCID record for Ming Zhao [Opens in a new window]
Guoqiang Tang
Affiliation:
DUT-UWA Joint Research Centre, State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, No. 2 Linggong Road, Dalian 116024, China
Liang Cheng*
Affiliation:
DUT-UWA Joint Research Centre, State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, No. 2 Linggong Road, Dalian 116024, China School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Perth, WA 6009, Australia
Feifei Tong*
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Perth, WA 6009, Australia
Lin Lu
Affiliation:
DUT-UWA Joint Research Centre, State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, No. 2 Linggong Road, Dalian 116024, China
Ming Zhao
Affiliation:
School of Computing, Engineering and Mathematics, Western Sydney University, Locked Bay 1797, Penrith, NSW 2751, Australia
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A numerical analysis of flow around a circular cylinder oscillating in-line with a steady flow is carried out over a range of driving frequencies 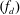$(f_{d})$ at relatively low amplitudes 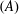$(A)$ and a constant Reynolds number of 175 (based on the free-stream velocity). The vortex shedding is investigated, especially when the shedding frequency 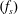$(f_{s})$ synchronises with the driving frequency. A series of modes of synchronisation are presented, which are referred to as the 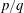$p/q$ modes, where 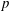$p$ and 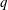$q$ are natural numbers. 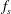When a $p/q$ mode occurs, $f_{s}$ is detuned to 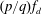$(p/q)f_{d}$, representing the shedding of 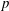$p$ pairs of vortices over 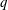$q$ cycles of cylinder oscillation. The 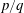$p/q$ modes are further characterised by the periodicity of the transverse force over every 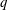$q$ cycles of oscillation and a spatial–temporal symmetry possessed by the global wake. The synchronisation modes 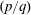$(p/q)$ with relatively small natural numbers are less sensitive to the change of external control parameters than those with large natural numbers, while the latter is featured with a narrow space of occurrence. Although the mode of synchronisation can be almost any rational ratio (as shown for 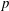$p$ and 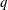$q$ smaller than 10), the probability of occurrence of synchronisation modes with 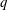$q$ being an even number is much higher than 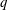$q$ being an odd number, which is believed to be influenced by the natural even distribution of vortices in the wake of a stationary cylinder.

JFM classification

Vortex Flows: Vortex dynamics Wakes/Jets: Vortex streets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 832 , 10 December 2017 , pp. 146 - 169
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Al-Mdallal, Q., Lawrence, K. & Kocabiyik, S. 2007 Forced streamwise oscillations of a circular cylinder: locked-on modes and resulting fluid forces. J. Fluids Struct. 23, 681–701.Google Scholar
Anagnostopoulos, P. 2000 Numerical study of the flow past a cylinder excited transversely to the incident stream. Part 1: lock-in zone, hydrodynamic forces and wake geometry. J. Fluids Struct. 14, 819–851.Google Scholar
Baek, S.-J. & Sung, H. J. 2000 Quasi-periodicity in the wake of a rotationally oscillating cylinder. J. Fluid Mech. 408, 275–300.CrossRefGoogle Scholar
Barbi, C., Favier, D., Maresca, C. & Telionis, D. 1986 Vortex shedding and lock-on of a circular cylinder in oscillatory flow. J. Fluid Mech. 170, 527–544.CrossRefGoogle Scholar
Bishop, R. & Hassan, A. 1964 The lift and drag forces on a circular cylinder oscillating in a flowing fluid. Proc. R. Soc. Lond. A 277, 51–75.Google Scholar
Blackburn, H. M. & Henderson, R. D. 1999 A study of two-dimensional flow past an oscillating cylinder. J. Fluid Mech. 385, 255–286.Google Scholar
Cantwell, C., Moxey, D., Comerford, A., Bolis, A., Rocco, G., Mengaldo, G., DE GRAZIA, D., Yakovlev, S., Lombard, J.-E. & Ekelschot, D. 2015 Nektar + +: an open-source spectral/hp element framework. Comput. Phys. Commun. 192, 205–219.CrossRefGoogle Scholar
Carberry, J., Sheridan, J. & Rockwell, D. 2005 Controlled oscillations of a cylinder: forces and wake modes. J. Fluid Mech. 538, 31–69.Google Scholar
Cetiner, O. & Rockwell, D. 2001 Streamwise oscillations of a cylinder in a steady current. Part 1. Locked-on states of vortex formation and loading. J. Fluid Mech. 427, 1–28.CrossRefGoogle Scholar
D’Adamo, J., Godoy-Diana, R. & Wesfreid, J. E. 2011 Spatiotemporal spectral analysis of a forced cylinder wake. Phys. Rev. E 84, 056308.Google Scholar
Detemple-Laake, E. & Eckelmann, H. 1989 Phenomenology of Kármán vortex streets in oscillatory flow. Exp. Fluids 7, 217–227.CrossRefGoogle Scholar
Griffin, O. M. & Hall, M. 1991 Review – vortex shedding lock-on and flow control in bluff body wakes. J. Fluids Engng 113, 526–537.CrossRefGoogle Scholar
Griffin, O. M. & Ramberg, S. E. 1974 The vortex-street wakes of vibrating cylinders. J. Fluid Mech. 66, 553–576.Google Scholar
Griffin, O. M. & Ramberg, S. E. 1976 Vortex shedding from a cylinder vibrating in line with an incident uniform flow. J. Fluid Mech. 75, 257–271.Google Scholar
Jiang, H., Cheng, L., Draper, S., An, H. & Tong, F. 2016 Three-dimensional direct numerical simulation of wake transitions of a circular cylinder. J. Fluid Mech. 801, 353–391.CrossRefGoogle Scholar
Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97, 414–443.Google Scholar
Karniadakis, G. E. & Triantafyllou, G. S. 1989 Frequency selection and asymptotic states in laminar wakes. J. Fluid Mech. 199, 441–469.CrossRefGoogle Scholar
Konstantinidis, E. & Balabani, S. 2007 Symmetric vortex shedding in the near wake of a circular cylinder due to streamwise perturbations. J. Fluids Struct. 23, 1047–1063.Google Scholar
Konstantinidis, E. & Bouris, D. 2016 Vortex synchronization in the cylinder wake due to harmonic and non-harmonic perturbations. J. Fluid Mech. 804, 248–277.Google Scholar
Koopmann, G. 1967 The vortex wakes of vibrating cylinders at low Reynolds numbers. J. Fluid Mech. 28, 501–512.CrossRefGoogle Scholar
Leontini, J., Stewart, B., Thompson, M. & Hourigan, K. 2006 Wake state and energy transitions of an oscillating cylinder at low Reynolds number. Phys. Fluids 18, 067101.Google Scholar
Leontini, J. S., Lo Jacono, D. & Thompson, M. C. 2011 A numerical study of an inline oscillating cylinder in a free stream. J. Fluid Mech. 688, 551–568.Google Scholar
Leontini, J. S., Ll Jacono, D. & Thompson, M. C. 2013 Wake states and frequency selection of a streamwise oscillating cylinder. J. Fluid Mech. 730, 162–192.Google Scholar
Lotfy, A. & Rockwell, D. 1993 The near-wake of an oscillating trailing edge: mechanisms of periodic and aperiodic response. J. Fluid Mech. 251, 173–201.Google Scholar
Marzouk, O. A. & Nayfeh, A. H. 2009 Reduction of the loads on a cylinder undergoing harmonic in-line motion. Phys. Fluids 21, 083103.CrossRefGoogle Scholar
Mittal, S., Ratner, A., Hastreiter, D. & Tezduyar, T. E. 1991 Space-time finite element computation of incompressible flows with emphasis on flows involving oscillating cylinders. Intl Video J. Engng Res. 1, 83–96.Google Scholar
Morse, T. & Williamson, C. 2009 Prediction of vortex-induced vibration response by employing controlled motion. J. Fluid Mech. 634, 5–39.CrossRefGoogle Scholar
Nazarinia, M., Lo Jacono, D., Thompson, M. C. & Sheridan, J. 2012 Flow over a cylinder subjected to combined translational and rotational oscillations. J. Fluids Struct. 32, 135–145.Google Scholar
Newman, D. J. & Karniadakis, G. E. 1997 A direct numerical simulation study of flow past a freely vibrating cable. J. Fluid Mech. 344, 95–136.Google Scholar
Olinger, D. & Sreenivasan, K. 1988 Nonlinear dynamics of the wake of an oscillating cylinder. Phys. Rev. Lett. 60, 797.Google Scholar
Olinger, D. J. 1993 A low-dimensional model for chaos in open fluid flows. Phys. Fluids 5, 1947–1951.CrossRefGoogle Scholar
Olinger, D. J. 1998 A low-order model for vortex shedding patterns behind vibrating flexible cables. Phys. Fluids 10, 1953–1961.Google Scholar
Ongoren, A. & Rockwell, D. 1988a Flow structure from an oscillating cylinder Part 1. Mechanisms of phase shift and recovery in the near wake. J. Fluid Mech. 191, 197–223.Google Scholar
Ongoren, A. & Rockwell, D. 1988b Flow structure from an oscillating cylinder. Part 2: mode competition in the near wake. J. Fluid Mech. 191, 225–245.Google Scholar
Ott, E. 2002 Chaos in Dynamical Systems. Cambridge University Press.Google Scholar
Rao, A., Leontini, J., Thompson, M. & Hourigan, K. 2013 Three-dimensionality in the wake of a rotating cylinder in a uniform flow. J. Fluid Mech. 717, 1–29.Google Scholar
Sarpkaya, T., Bakinis, C. & Storm, M. A. 1984 Hydrodynamic forces from combined wave and current flow on smooth and rough circular cylinders at high Reynolds numbers. In Ocean Technology Conference, Houston, TX, October, p. 4830.Google Scholar
Stansby, P. 1976 The locking-on of vortex shedding due to the cross-stream vibration of circular cylinders in uniform and shear flows. J. Fluid Mech. 74, 641–665.Google Scholar
Tang, G., Cheng, L., Lu, L., Zhao, M., Tong, F. & Dong, G. 2016 Vortex formation in the wake of a streamwisely oscillating cylinder in steady flow. In Fluid–Structure–Sound Interactions and Control (ed. Zhou, Y., Lucey, A., Liu, Y. & Huang, L.), Springer.Google Scholar
Tanida, Y., Okajima, A. & Watanabe, Y. 1973 Stability of a circular cylinder oscillating in uniform flow or in a wake. J. Fluid Mech. 61, 769–784.Google Scholar
Tatsuno, M. 1972 Vortex streets behind a circular cylinder oscillating in the direction of flow. Bull. Res. Inst. Appl. Mech. Kyushu Univ. 36, 25–37.Google Scholar
Tatsuno, M. & Bearman, P. 1990 A visual study of the flow around an oscillating circular cylinder at low Keulegan–Carpenter numbers and low Stokes numbers. J. Fluid Mech. 211, 157–182.Google Scholar
Tong, F., Cheng, L., Xiong, C., Draper, S., An, H. & Lou, X. 2017 Flow regimes for a square cross-section cylinder in oscillatory flow. J. Fluid Mech. 813, 85–109.Google Scholar
Tong, F., Cheng, L., Zhao, M. & An, H. 2015 Oscillatory flow regimes around four cylinders in a square arrangement under small KC and Re conditions. J. Fluid Mech. 769, 298–336.Google Scholar
Tudball-Smith, D., Leontini, J. S., Sheridan, J. & Lo Jacono, D. 2012 Streamwise forced oscillations of circular and square cylinders. Phys. Fluids 24, 111703.Google Scholar
Williamson, C. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2, 355–381.CrossRefGoogle Scholar
Williamson, C. H. K. & Brown, G. L. 1998 A series in 1/√Re to represent the Strouhal–Reynolds number relationship of the cylinder wake. J. Fluids Struct. 12, 1073–1085.Google Scholar
Woo, H. 1999 A note on phase-locked states at low Reynolds numbers. J. Fluids Struct. 13, 153–158.Google Scholar
Wu, J.-Z., Lu, X.-Y., Denny, A. G., Fan, M. & Wu, J.-M. 1998 Post-stall flow control on an airfoil by local unsteady forcing. J. Fluid Mech. 371, 21–58.Google Scholar
Xu, S., Zhou, Y. & Wang, M. 2006 A symmetric binary-vortex street behind a longitudinally oscillating cylinder. J. Fluid Mech. 556, 27–43.CrossRefGoogle Scholar
Zdravkovich, M. 1996 Different modes of vortex shedding: an overview. J. Fluids Struct. 10, 427–437.CrossRefGoogle Scholar