Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Campagnolo, Filippo
Tamaro, Simone
Mühle, Franz
and
Bottasso, Carlo L.
2023.
Wind Tunnel Testing of Combined Derating and Wake Steering.
IFAC-PapersOnLine,
Vol. 56,
Issue. 2,
p.
8400.
Wei, Nathaniel J.
and
Dabiri, John O.
2023.
Power-generation enhancements and upstream flow properties of turbines in unsteady inflow conditions.
Journal of Fluid Mechanics,
Vol. 966,
Issue. ,
Lu, Jianfeng
Li, Chao
Li, Xiang
Liu, Haoyang
Zhang, Gengsheng
Liu, Nansheng
and
Liu, Luoqin
2023.
Analytical model for the power production of a yaw-misaligned wind turbine.
Physics of Fluids,
Vol. 35,
Issue. 12,
Liew, Jaime
Heck, Kirby S.
and
Howland, Michael F.
2024.
Unified momentum model for rotor aerodynamics across operating regimes.
Nature Communications,
Vol. 15,
Issue. 1,
Li, Zhaobin
and
Yang, Xiaolei
2024.
Resolvent-based motion-to-wake modelling of wind turbine wakes under dynamic rotor motion.
Journal of Fluid Mechanics,
Vol. 980,
Issue. ,
Heck, Kirby S.
Liew, Jaime
and
Howland, Michael F.
2024.
Investigation of far-wake models coupled with yaw-induction control for power optimization.
Journal of Physics: Conference Series,
Vol. 2767,
Issue. 9,
p.
092103.
van den Broek, Maarten J.
Becker, Marcus
Sanderse, Benjamin
and
van Wingerden, Jan-Willem
2024.
Dynamic wind farm flow control using free-vortex wake models.
Wind Energy Science,
Vol. 9,
Issue. 3,
p.
721.
Astolfi, Davide
De Caro, Fabrizio
Pasetti, Marco
Gao, Linyue
Pandit, Ravi
Vaccaro, Alfredo
and
Hong, Jiarong
2024.
Investigation of Wind Turbine Static Yaw Error Based on Utility-Scale Controlled Experiments.
IEEE Transactions on Industry Applications,
Vol. 60,
Issue. 4,
p.
6559.
Li, Chao
Liu, Luoqin
and
Lu, Xiyun
2024.
A grouping strategy for reinforcement learning-based collective yaw control of wind farms.
Theoretical and Applied Mechanics Letters,
Vol. 14,
Issue. 1,
p.
100491.
Dallas, Scott
Stock, Adam
and
Hart, Edward
2024.
Control-oriented modelling of wind direction variability.
Wind Energy Science,
Vol. 9,
Issue. 4,
p.
841.
Hulsman, P.
Howland, M.
Göçmen, T.
Petrović, V.
and
Kühn, M.
2024.
Self-Learning Data-Driven Wind Farm Control Strategy Using Field Measurements.
p.
1057.
Kayedpour, Nezmin
Kooning, Jeroen D. M. De
Samani, Arash E.
Kayedpour, Farjam
Vandevelde, Lieven
and
Crevecoeur, Guillaume
2024.
An Optimal Wind Farm Operation Strategy for the Provision of Frequency Containment Reserve Incorporating Active Wake Control.
IEEE Transactions on Sustainable Energy,
Vol. 15,
Issue. 1,
p.
276.
Bempedelis, Nikolaos
Gori, Filippo
Wynn, Andrew
Laizet, Sylvain
and
Magri, Luca
2024.
Data-driven optimisation of wind farm layout and wake steering with large-eddy simulations.
Wind Energy Science,
Vol. 9,
Issue. 4,
p.
869.
Jané‐Ippel, Christian
Bempedelis, Nikos
Palacios, Rafael
and
Laizet, Sylvain
2024.
Bayesian Optimisation of a Two‐Turbine Configuration Around a 2D Hill Using Large Eddy Simulations.
Wind Energy,
Vol. 27,
Issue. 11,
p.
1412.
Tamaro, Simone
Campagnolo, Filippo
and
Bottasso, Carlo L.
2024.
On the power and control of a misaligned rotor – beyond the cosine law.
Wind Energy Science,
Vol. 9,
Issue. 7,
p.
1547.
Hulsman, P.
Howland, M.
Göçmen, T.
and
Petrović, V.
2024.
Assessing Closed-Loop Data-Driven Wind Farm Control Strategies within a Wind Tunnel.
Journal of Physics: Conference Series,
Vol. 2767,
Issue. 3,
p.
032049.
Liew, Jaime
Heck, Kirby
and
Howland, Michael F.
2024.
Enhanced Modeling of Joint Yaw and Axial Induction Control Using Blade Element Momentum Methods.
Journal of Physics: Conference Series,
Vol. 2767,
Issue. 3,
p.
032018.
Catania, M.
Pomaranzi, G.
Fontanella, A.
and
Zasso, A.
2024.
Modelling of Wind Turbines as Porous Disks for Wind Farm Flow Studies.
Journal of Physics: Conference Series,
Vol. 2767,
Issue. 5,
p.
052049.
Wei, Nathaniel J.
El Makdah, Adnan
Hu, JiaCheng
Kaiser, Frieder
Rival, David E.
and
Dabiri, John O.
2024.
Wake dynamics of wind turbines in unsteady streamwise flow conditions.
Journal of Fluid Mechanics,
Vol. 1000,
Issue. ,
Meneveau, Charles
2024.
The fluid mechanics of active flow control at very large scales.
Journal of Fluid Mechanics,
Vol. 1000,
Issue. ,
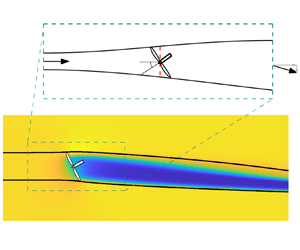
 $\gamma$) and thrust coefficient. The analytical model is validated against large eddy simulations of a yawed actuator disk. Because the induction depends on the yaw and thrust coefficient, the power generated by a yawed actuator disk will always be greater than a
$\gamma$) and thrust coefficient. The analytical model is validated against large eddy simulations of a yawed actuator disk. Because the induction depends on the yaw and thrust coefficient, the power generated by a yawed actuator disk will always be greater than a  $\cos ^3(\gamma )$ model suggests. The power lost due to yaw misalignment depends on the thrust coefficient. An analytical expression for the thrust coefficient that maximizes power, depending on the yaw, is developed and validated. Finally, using the developed induction model as an initial condition for a turbulent far-wake model, we demonstrate how combining wake steering and thrust (induction) control can increase array power, compared to either independent steering or induction control, due to the joint dependence of the induction on the thrust coefficient and yaw angle.
$\cos ^3(\gamma )$ model suggests. The power lost due to yaw misalignment depends on the thrust coefficient. An analytical expression for the thrust coefficient that maximizes power, depending on the yaw, is developed and validated. Finally, using the developed induction model as an initial condition for a turbulent far-wake model, we demonstrate how combining wake steering and thrust (induction) control can increase array power, compared to either independent steering or induction control, due to the joint dependence of the induction on the thrust coefficient and yaw angle.


