Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Reinhardt, Yvonne
Meinen, Niklaus
and
Meyer, Daniel W.
2013.
Modeling anisotropic Reynolds-stress dissipation in particle- or droplet-laden flows.
International Journal of Multiphase Flow,
Vol. 56,
Issue. ,
p.
1.
Meyer, Daniel W.
and
Eggersdorfer, Maximilian L.
2014.
Simulating particle collisions in homogeneous turbulence with kinematic simulation – A validation study.
Colloids and Surfaces A: Physicochemical and Engineering Aspects,
Vol. 454,
Issue. ,
p.
57.
Saber, Ammar
Lundström, T. Staffan
and
Hellström, J. Gunnar I.
2015.
Turbulent Modulation in Particulate Flow: A Review of Critical Variables.
Engineering,
Vol. 07,
Issue. 10,
p.
597.
Saber, Ammar
Staffan Lundström, T.
and
Hellström, J. Gunnar I.
2016.
Influence of Inertial Particles on Turbulence Characteristics in Outer and Near Wall Flow as Revealed With High Resolution Particle Image Velocimetry.
Journal of Fluids Engineering,
Vol. 138,
Issue. 9,
Meyer, Daniel W.
and
Saggini, Frédéric
2016.
Testing the Markov hypothesis in fluid flows.
Physical Review E,
Vol. 93,
Issue. 5,
Pakhomov, Maksim A.
and
Terekhov, Viktor I.
2017.
The Effect of Droplets Evaporation on Turbulence Modification and Heat Transfer Enhancement in a Two-Phase Mist Flow Downstream of a Pipe Sudden Expansion.
Flow, Turbulence and Combustion,
Vol. 98,
Issue. 1,
p.
341.
Pakhomov, M. A.
and
Terekhov, V. I.
2017.
Solid particle spreading in gas-dispersed confined swirling flow. Eulerian and Lagrangian approaches.
Thermophysics and Aeromechanics,
Vol. 24,
Issue. 3,
p.
325.
Battista, F.
Gualtieri, P.
Mollicone, J.-P.
and
Casciola, C.M.
2018.
Application of the Exact Regularized Point Particle method (ERPP) to particle laden turbulent shear flows in the two-way coupling regime.
International Journal of Multiphase Flow,
Vol. 101,
Issue. ,
p.
113.
Kasbaoui, M. Houssem
Koch, Donald L.
and
Desjardins, Olivier
2019.
Clustering in Euler–Euler and Euler–Lagrange simulations of unbounded homogeneous particle-laden shear.
Journal of Fluid Mechanics,
Vol. 859,
Issue. ,
p.
174.
Battista, F.
Mollicone, J.-P.
Gualtieri, P.
Messina, R.
and
Casciola, C. M.
2019.
Exact regularised point particle (ERPP) method for particle-laden wall-bounded flows in the two-way coupling regime.
Journal of Fluid Mechanics,
Vol. 878,
Issue. ,
p.
420.
Pakhomov, M.A.
and
Terekhov, V.I.
2020.
Numerical analysis of swirling turbulent droplet-laden flow and heat transfer in a sudden pipe expansion.
International Journal of Heat and Fluid Flow,
Vol. 85,
Issue. ,
p.
108681.
Shi, Pengyu
Sommer, Anna-Elisabeth
Rox, Hannes
Eckert, Kerstin
and
Rzehak, Roland
2022.
Euler-Euler/RANS modeling of solid-liquid flow in stirred tanks: A comprehensive model validation.
Minerals Engineering,
Vol. 185,
Issue. ,
p.
107679.
Battista, F.
Gualtieri, P.
Mollicone, J.-P.
Salvadore, F.
and
Casciola, C. M.
2023.
Drag increase and turbulence augmentation in two-way coupled particle-laden wall-bounded flows.
Physics of Fluids,
Vol. 35,
Issue. 4,
Weiss, Philipp
Meyer, Daniel W.
and
Jenny, Patrick
2023.
Understanding the role of droplet clusters in a reactive mixing layer.
Physics of Fluids,
Vol. 35,
Issue. 10,
Wang, Ya
Xiao, Hualin
Chai, Min
Liu, Kai
Luo, Kun
and
Fan, Jianren
2023.
DNS analysis of turbulence modulation by lean premixed prevaporized spray flames in a model combustor.
Proceedings of the Combustion Institute,
Vol. 39,
Issue. 2,
p.
2703.
Shuai, Shuai
Roy, Anubhab
and
Kasbaoui, M. Houssem
2024.
The merger of co-rotating vortices in dusty flows.
Journal of Fluid Mechanics,
Vol. 981,
Issue. ,
Pakhomov, Maksim A.
2024.
RANS simulation of heat transfer in a mist turbulent flow over an obstacle.
International Journal of Thermal Sciences,
Vol. 199,
Issue. ,
p.
108913.
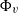 ${\Phi }_{v} $ and therefore may be important when simulating such flows. In this work, a modelling framework that accounts for preferential concentration and reproduces isotropic and anisotropic turbulence attenuation effects is presented. The framework is outlined for both Reynolds-averaged Navier–Stokes (RANS) and joint probability density function (p.d.f.) methods. Validations are performed involving a range of particle and flow-field parameters and are based on the direct numerical simulation (DNS) study of Boivin, Simonin & Squires (J. Fluid Mech., vol. 375, 1998, pp. 235–263) dealing with heavy particles suspended in homogeneous isotropic turbulence (Stokes number
${\Phi }_{v} $ and therefore may be important when simulating such flows. In this work, a modelling framework that accounts for preferential concentration and reproduces isotropic and anisotropic turbulence attenuation effects is presented. The framework is outlined for both Reynolds-averaged Navier–Stokes (RANS) and joint probability density function (p.d.f.) methods. Validations are performed involving a range of particle and flow-field parameters and are based on the direct numerical simulation (DNS) study of Boivin, Simonin & Squires (J. Fluid Mech., vol. 375, 1998, pp. 235–263) dealing with heavy particles suspended in homogeneous isotropic turbulence (Stokes number  $\mathit{St}= O(1{\unicode{x2013}} 10)$, particle/fluid density ratio
$\mathit{St}= O(1{\unicode{x2013}} 10)$, particle/fluid density ratio 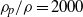 ${\rho }_{p} / \rho = 2000$,
${\rho }_{p} / \rho = 2000$,  ${\Phi }_{v} = O(1{0}^{- 4} )$) and the experimental investigation of Poelma, Westerweel & Ooms (J. Fluid Mech., vol. 589, 2007, pp. 315–351) involving light particles (
${\Phi }_{v} = O(1{0}^{- 4} )$) and the experimental investigation of Poelma, Westerweel & Ooms (J. Fluid Mech., vol. 589, 2007, pp. 315–351) involving light particles ( $\mathit{St}= O(0. 1)$,
$\mathit{St}= O(0. 1)$, 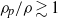 ${\rho }_{p} / \rho \gtrsim 1$,
${\rho }_{p} / \rho \gtrsim 1$, 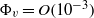 ${\Phi }_{v} = O(1{0}^{- 3} )$) settling in grid turbulence. The development in this work is restricted to volume loadings where particle or droplet collisions are negligible.
${\Phi }_{v} = O(1{0}^{- 3} )$) settling in grid turbulence. The development in this work is restricted to volume loadings where particle or droplet collisions are negligible.

