Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-12-03T20:40:40.812Z Has data issue: false hasContentIssue false
  • English
  • Français

Modelling a surfactant-covered droplet on a solid surface in three-dimensional shear flow

Published online by Cambridge University Press:  18 June 2020

Haihu Liu Open the ORCID record for Haihu Liu [Opens in a new window] ,
Jinggang Zhang ,
Yan Ba ,
Ningning Wang  and
Lei Wu Open the ORCID record for Lei Wu [Opens in a new window]
Haihu Liu*
Affiliation:
School of Energy and Power Engineering, Xi’an Jiaotong University, 28 West Xianning Road, Xi’an 710049, China
Jinggang Zhang
Affiliation:
School of Energy and Power Engineering, Xi’an Jiaotong University, 28 West Xianning Road, Xi’an 710049, China
Yan Ba
Affiliation:
School of Astronautics, Northwestern Polytechnical University, 127 West Youyi Road,Xi’an710072, China
Ningning Wang
Affiliation:
School of Energy and Power Engineering, Xi’an Jiaotong University, 28 West Xianning Road, Xi’an 710049, China
Lei Wu
Affiliation:
Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen518055, China
*
† Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

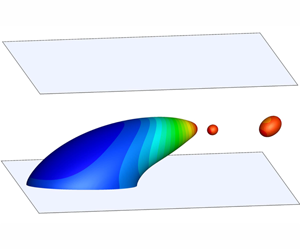
A surfactant-covered droplet on a solid surface subject to a three-dimensional shear flow is studied using a lattice-Boltzmann and finite-difference hybrid method, which allows for the surfactant concentration beyond the critical micelle concentration. We first focus on low values of the effective capillary number ($Ca_{e}$) and study the effect of $Ca_{e}$, viscosity ratio ($\unicode[STIX]{x1D706}$) and surfactant coverage on the droplet behaviour. Results show that at low $Ca_{e}$ the droplet eventually reaches steady deformation and a constant moving velocity $u_{d}$. The presence of surfactants not only increases droplet deformation but also promotes droplet motion. For each $\unicode[STIX]{x1D706}$, a linear relationship is found between contact-line capillary number and $Ca_{e}$, but not between wall stress and $u_{d}$ due to Marangoni effects. As $\unicode[STIX]{x1D706}$ increases, $u_{d}$ decreases monotonically, but the deformation first increases and then decreases for each $Ca_{e}$. Moreover, increasing surfactant coverage enhances droplet deformation and motion, although the surfactant distribution becomes less non-uniform. We then increase $Ca_{e}$ and study droplet breakup for varying $\unicode[STIX]{x1D706}$, where the role of surfactants on the critical $Ca_{e}$ ($Ca_{e,c}$) of droplet breakup is identified by comparing with the clean case. As in the clean case, $Ca_{e,c}$ first decreases and then increases with increasing $\unicode[STIX]{x1D706}$, but its minima occurs at $\unicode[STIX]{x1D706}=0.5$ instead of $\unicode[STIX]{x1D706}=1$ in the clean case. The presence of surfactants always decreases $Ca_{e,c}$, and its effect is more pronounced at low $\unicode[STIX]{x1D706}$. Moreover, a decreasing viscosity ratio is found to favour ternary breakup in both clean and surfactant-covered cases, and tip streaming is observed at the lowest $\unicode[STIX]{x1D706}$ in the surfactant-covered case.

JFM classification

Interfacial Flows (free surface): Contact lines Drops and Bubbles: Breakup/coalescence Convection: Marangoni convection
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 897 , 25 August 2020 , A33
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ashgriz, N. & Mashayek, F. 1995 Temporal analysis of capillary jet breakup. J. Fluid Mech. 291, 163–190.CrossRefGoogle Scholar
Bel Fdhila, R. & Duineveld, P. C. 1996 The effect of surfactant on the rise of a spherical bubble at high Reynolds and Peclet numbers. Phys. Fluids 8, 310–321.CrossRefGoogle Scholar
Binks, B. P., Fletcher, P. D. I., Holt, B. L., Beaussoubre, P. & Wong, K. 2010 Selective retardation of perfume oil evaporation from oil-in-water emulsions stabilized by either surfactant or nanoparticles. Langmuir 26 (23), 18024–18030.CrossRefGoogle ScholarPubMed
Booty, M. R. & Siegel, M. 2005 Steady deformation and tip-streaming of a slender bubble with surfacants in an extensional flow. J. Fluid Mech. 544, 243–275.CrossRefGoogle Scholar
Chan, K. Y. & Borhan, A. 2006 Spontaneous spreading of surfactant-bearing drops in the sorption-controlled limit. J. Colloid Interface Sci. 302, 374–377.CrossRefGoogle ScholarPubMed
Chen, J. & Stebe, K. J. 1996 Marangoni retardation of the terminal velocity of a settling droplet: the role of surfactant physico-chemistry. J. Colloid Interface Sci. 178 (1), 144–155.CrossRefGoogle Scholar
Clay, M. A. & Miksis, M. J. 2004 Effects of surfactant on droplet spreading. Phys. Fluids 16 (8), 3070–3078.CrossRefGoogle Scholar
Craster, R. V. & Matar, O. K. 2009 Dynamics and stability of thin liquid films. Rev. Mod. Phys. 81 (3), 1131–1198.CrossRefGoogle Scholar
De Bruijn, R. A. 1993 Tipstreaming of drops in simple shear flows. Chem, Eng. Ssi. 48 (2), 277–284.CrossRefGoogle Scholar
D’humières, D., Ginzburg, I., Krafczyk, M., Lallemand, P. & Luo, L.-S. 2002 Multiple-relaxation-time lattice Boltzmann models in three dimensions. Phil. Trans. R. Soc. Lond. A 360, 437–451.CrossRefGoogle ScholarPubMed
Dimitrakopoulos, P. 2007 Deformation of a droplet adhering to a solid surface in shear flow: onset of interfacial sliding. J. Fluid Mech. 580, 451–466.CrossRefGoogle Scholar
Dimitrakopoulos, P. & Higdon, J. J. L. 1998 On the displacement of three-dimensional fluid droplets from solid surfaces in low-Reynolds-number shear flows. J. Fluid Mech. 377, 189–222.CrossRefGoogle Scholar
Ding, H., Gilani, M. N. H. & Spelt, P. D. M. 2010 Sliding, pinch-off and detachment of a drop on a wall in shear flow. J. Fluid Mech. 644, 217–244.CrossRefGoogle Scholar
Ding, H. & Spelt, P. D. M. 2007 Wetting condition in diffuse interface simulations of contact line motion. Phys. Rev. E 75 (4), 046708.Google ScholarPubMed
Ding, H. & Spelt, P. D. M. 2008 Onset of motion of a three-dimensional droplet on a wall in shear flow at moderate Reynolds numbers. J. Fluid Mech. 599, 341–362.CrossRefGoogle Scholar
Ding, H., Zhu, X., Gao, P. & Lu, X.-Y. 2018 Ratchet mechanism of drops climbing a vibrated oblique plate. J. Fluid Mech. 835, R1.CrossRefGoogle Scholar
Edmonstone, B. D., Matar, O. K. & Craster, R. V. 2006 A note on the coating of an inclined plane in the presence of soluble surfactant. J. Colloid Inerface Sci. 293 (1), 222–229.CrossRefGoogle ScholarPubMed
Eggleton, C. D., Tsai, T.-M. & Stebe, K. 2001 Tip streaming from a drop in the presence of surfactants. Phys. Rev. Lett. 87 (4), 048302.CrossRefGoogle ScholarPubMed
Ganesan, S. 2013 On the dynamic contact angle in simulation of impinging droplets with sharp interface methods. Microfluid. Nanofluid. 14 (3-4), 615–625.CrossRefGoogle Scholar
Ginzburg, I. & d’Humières, D. 2003 Multireflection boundary conditions for lattice Boltzmann models. Phys. Rev. E 68 (6), 066614.Google ScholarPubMed
Griffith, R. M. 1962 The effect of surfactants on the terminal velocity of drops and bubbles. Chem. Engng Sci. 17 (12), 1057–1070.CrossRefGoogle Scholar
Guo, Z., Zheng, C. & Shi, B. 2002 Discrete lattice effects on the forcing term in the lattice Boltzmann method. Phys. Rev. E 65 (4), 046308.Google ScholarPubMed
Gupta, A. K. & Basu, S. 2008 Deformation of an oil droplet on a solid substrate in simple shear flow. Chem. Engng Sci. 63 (22), 5496–5502.CrossRefGoogle Scholar
Hou, B., Wang, Y., Cao, X., Zhang, J., Song, X., Ding, M. & Chen, W. 2016 Mechanisms of enhanced oil recovery by surfactant-induced wettability alteration. J. Dispersion Sci. Technol. 37, 1259–1267.CrossRefGoogle Scholar
Huang, J.-J., Huang, H. & Wang, X. 2014 Numerical study of drop motion on a surface with stepwise wettability gradient and contact angle hysteresis. Phys. Fluids 26, 062101.CrossRefGoogle Scholar
Jensen, O. E. & Naire, S. 2006 The spreading and stability of a surfactant-laden drop on a prewetted substrate. J. Fluid Mech. 554, 5–24.CrossRefGoogle Scholar
Jensen, P. J. A., Vananroye, A., Moldenaers, P. & Anderson, P. D. 2010 Generalized behavior of the breakup of viscous drops in confinements. J. Rheol. 54 (5), 1047–1060.CrossRefGoogle Scholar
Jiang, G.-S. & Shu, C.-W. 1996 Effcient implementation of weight ENO schemes. J. Comput. Phys. 126, 202–228.CrossRefGoogle Scholar
Jiang, J., Sun, Z. & Santamarina, J. C. 2016 Capillary pressure across a pore throat in the presence of surfactants. Water Resour. Res. 52 (12), 9586–9599.CrossRefGoogle Scholar
Karapetsas, G., Craster, R. V. & Matar, O. K. 2011a On surfactant-enhanced spreading and superspreading of liquid drops on solid surfaces. J. Fluid Mech. 670, 5–37.CrossRefGoogle Scholar
Karapetsas, G., Craster, R. V. & Matar, O. K. 2011b Surfactant-driven dynamics of liquid lenses. Phys. Fluids 23, 122106.CrossRefGoogle Scholar
af Klinteberg, L., Lindbo, D. & Tornberg, A.-K. 2014 An explicit Eulerian method for multiphase flow with contact line dynamics and insoluble surfactant. Comput. Fluids 101, 50–63.CrossRefGoogle Scholar
Kovalchuk, N. M., Roumpea, E., Nowak, E., Chinaud, M., Angeli, P. & Simmons, M. J. H. 2018 Effect of surfactant on emulsification in microchannels. Chem. Engng Sci. 176, 139–152.CrossRefGoogle Scholar
Ladd, A. J. C. 1994 Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. J. Fluid Mech. 271, 285–309.CrossRefGoogle Scholar
Lai, M.-C., Tseng, Y.-H. & Huang, H. 2010 Numerical simulation of moving contact lines with surfactant by immersed boundary method. Commun. Comput. Phys. 8 (4), 735–757.CrossRefGoogle Scholar
Li, Y., Wang, K. & Luo, G. 2017 Microdroplet generation with dilute surfactant concentration in a modified T-junction device. Ind. Engng Chem. Res. 56 (42), 12131–12138.CrossRefGoogle Scholar
Liang, H., Chai, Z. H., Shi, B. C., Guo, Z. L. & Zhang, T. 2014 Phase-field-based lattice Boltzmann model for axisymmetric multiphase flows. Phys. Rev. E 90, 063311.Google ScholarPubMed
Liu, C.-Y., Vandre, E., Carvalho, M. S. & Kumar, S. 2016a Dynamic wetting failure and hydrodynamic assist in curtain coating. J. Fluid Mech. 808, 290–315.CrossRefGoogle Scholar
Liu, C.-Y., Vandre, E., Carvalho, M. S. & Kumar, S. 2016b Dynamic wetting failure in surfactant solutions. J. Fluid Mech. 789, 285–309.CrossRefGoogle Scholar
Liu, H., Ba, Y., Wu, L., Li, Z., Xi, G. & Zhang, Y. 2018 A hybrid lattice Boltzmann and finite difference method for droplet dynamics with insoluble surfactants. J. Fluid Mech. 837, 381–412.CrossRefGoogle Scholar
Liu, H., Valocchi, A. J. & Kang, Q. 2012 Three-dimensional lattice Boltzmann model for immiscible two-phase flow simulations. Phys. Rev. E 85 (4), 046309.Google ScholarPubMed
Liu, H., Wu, L., Ba, Y., Xi, G. & Zhang, Y. 2016c A lattice Boltzmann method for axisymmetric multicomponent flows with high viscosity ratio. J. Comput. Phys. 327, 873–893.CrossRefGoogle Scholar
Ngangia, H., Young, Y.-N., Vlahovska, P. M. & Blawzdziewicz, J. 2013 Equilibrium electro-deformation of a surfactant-laden viscous drop. Phys. Fluids 25, 092106.Google Scholar
Nikolov, A. & Wasan, D. 2015 Current opinion in superspreading mechanisms. Adv. Colloid Interface Sci. 222, 517–529.CrossRefGoogle ScholarPubMed
Palaparthi, R., Papageorgiou, D. T. & Maldarelli, C. 2006 Theory and experiments on the stagnant cap regime in the motion of spherical surfactant-laden bubbles. J. Fluid Mech. 559, 1–44.CrossRefGoogle Scholar
Paratap, V., Moumen, N. & Sbramanian, R. S. 2008 Thermocapillary motion of a liquid drop on a horizontl solid surface. Langmuir 24 (9), 5185–5193.CrossRefGoogle Scholar
Pawar, Y. & Stebe, K. J. 1996 Marangoni effects on drop deformation in an extensional flow: The role of surfactant physical chemistry. i. insoluble surfactants. Phys. Fluids 8, 1738–1751.CrossRefGoogle Scholar
Poddar, A., Mandal, S., Bandopadhyay, A. & Chakraborty, S. 2018 Sedimentation of a surfactant-laden drop under the influence of an electric field. J. Fluid Mech. 849, 277–311.CrossRefGoogle Scholar
Rafaï, S., Sarker, D., Bergeron, V., Meunier, J. & Bonn, D. 2002 Superspreading: aqueous surfactant drops spreading on hydrophobic surfaces. Langmuir 18 (26), 10486–10488.CrossRefGoogle Scholar
Rayleigh, Lord 1878 On the instability of jets. Proc. Lond. Math. Soc. 10, 4–13.CrossRefGoogle Scholar
Riaud, A., Zhang, H., Wang, X., Wang, K. & Luo, G. 2018 Numerical study of surfactant dynamics during emulsification in a T-junction microchannel. Langmuir 34 (17), 4980–4990.CrossRefGoogle Scholar
Roumpea, E., Kovalchuk, N. M., Chinaud, M., Nowak, E., Simmons, M. J. H. & Angeli, P. 2019 Experimental studies on droplet formation in a flow-focusing microchannel in the presence of surfactants. Chem. Engng Sci. 195, 507–518.CrossRefGoogle Scholar
Schleizer, A. D. & Bonnecaze, R. T. 1999 Displacement of a two-dimensional immiscible droplet adhering to a wall in shear and pressure-driven flows. J. Fluid Mech. 383, 29–54.CrossRefGoogle Scholar
Schunk, P. R. & Scriven, L. E. 1997 Surfactant effects in coating processes. In Liquid Film Coating, pp. 495–536. Chapman and Hall.CrossRefGoogle Scholar
Shah, D. O. & Schechter, R. S. 2012 Improved Oil Recovery by Surfactant and Polymer Flooding, Elsevier.Google Scholar
Spelt, P. D. M. 2006 Shear flow past two-dimensional droplets pinned or moving on an adhering channel wall at moderate Reynolds numbers: a numerical study. J. Fluid Mech. 561, 439–463.CrossRefGoogle Scholar
Stone, H. A. 1994 Dynamics of drop deformation and breakup in viscous fluids. Annu. Rev. Fluid Mech. 26, 65–102.CrossRefGoogle Scholar
Stone, H. A. & Leal, L. G. 1990 The effects of surfactants on drop deformation and breakup. J. Fluid Mech. 220, 161–186.CrossRefGoogle Scholar
Sugiyama, K. & Sbragaglia, M. 2008 Linear shear flow past a hemispherical droplet adhering to a solid surface. J. Engng Maths 62 (1), 35–50.CrossRefGoogle Scholar
Sui, Y., Ding, H. & Spelt, P. D. M. 2014 Numerical simulations of flows with moving contact lines. Annu. Rev. Fluid Mech. 46, 97–119.CrossRefGoogle Scholar
Tan, C. S., Gee, M. L. & Stevens, G. W. 2003 Optically profiling a draining aqueous film confined between an oil droplet and a solid surface: effect of nonionic surfactant. Langmuir 19 (19), 7911–7918.CrossRefGoogle Scholar
Tang, X., Xiao, S., Lei, Q., Yuan, L., Peng, B., He, L., Luo, J. & Pei, Y. 2019 Molecular dynamics simulation of surfactant flooding driven oil-detachment in nano-silica channels. J. Phys. Chem. B 123 (1), 277–288.CrossRefGoogle ScholarPubMed
Taylor, G. I. 1934 The formation of emulsions in definable fields of flow. Proc. R. Soc. Lond. A 146 (858), 501–523.Google Scholar
Teigen, K. E., Li, X., Lowengrub, J., Wang, F. & Voigt, A. 2009 A diffuse-interface approach for modelling transport, diffusion and adsorption/desorption of material euantities on a deformation interface. Commun. Math. Sci. 4, 1009–1037.Google Scholar
Teigen, K. E., Song, P., Lowengrub, J. & Voigt, A. 2011 A diffuse-interface method for two-phase flows with soluble surfactants. J. Comput. Phys. 230 (2), 375–393.CrossRefGoogle ScholarPubMed
Tjahjadi, M., Stone, H. A. & Ottino, J. M. 1992 Satellite and subsatellite formation in capillary breakup. J. Fluid Mech. 243, 297–317.CrossRefGoogle Scholar
Vananroye, A., Cardinaels, R., Puyvelde, P. V. & Moldenaers, P. 2008 Effect of confinement and viscosity ratio on the dynamics of single droplets during transient shear flow. J. Rheol. 52 (6), 1459–1475.CrossRefGoogle Scholar
Vananroye, A., Puyvelde, P. V. & Moldenaers, P. 2007 Effect of confinement on the steady-state behavior of single droplets during shear flow. J. Rheol. 51 (1), 139–153.CrossRefGoogle Scholar
Wang, N., Liu, H. & Zhang, C. 2017 Deformation and breakup of a confined droplet in shear flows with power-law rheology. J. Rheol. 61 (4), 741–758.CrossRefGoogle Scholar
Wei, B., Hou, J., Sukop, M. C. & Liu, H. 2019 Pore scale study of amphiphilic fluids flow using the Lattice Boltzmann model. Intl J. Heat Mass Transfer 139, 725–735.CrossRefGoogle Scholar
Wei, H.-H. 2018 Marangoni-enhanced capillary wetting in surfactant-driven superspreading. J. Fluid Mech. 855, 181–209.CrossRefGoogle Scholar
Weidner, D. E. 2012 The effect of surfactant convection and diffusion on the evolution of an axisymmetric pendant droplet. Phys. Fluids 24, 062104.CrossRefGoogle Scholar
Xu, J.-J., Li, Z., Lowengrub, J. & Zhao, H. 2006 A level-set method for interfacial flows with surfactant. J. Comput. Phys. 212 (2), 590–616.CrossRefGoogle Scholar
Xu, J.-J. & Ren, W. 2014 A level-set method for two-phase flows with moving contact line and insoluble surfactant. J. Comput. Phys. 263, 71–90.CrossRefGoogle Scholar
Xu, J.-J. & Zhao, H. K. 2003 An Eulerian formulation for solving partial differential equations along a moving interface. J. Sci. Comput. 19 (1–3), 573–594.CrossRefGoogle Scholar
Xu, Z., Liu, H. & Valocchi, A. J. 2017 Lattice Boltzmann simulation of immiscible two-phase flow with capillary valve effect in porous media. Water Resour. Res. 53 (5), 3770–3790.CrossRefGoogle Scholar
Yon, S. & Pozrikidis, C. 1999 Deformation of a liquid drop adhering to a plane wall: significance of the drop viscosity and the effect of an insoluble surfactant. Phys. Fluids 11 (6), 1297–1308.CrossRefGoogle Scholar
Young, Y.-N., Booty, M. R., Siegel, M. & Li, J. 2009 Influence of surfactant solubility on the deformation and breakup of a bubble or capillary jet in a viscous fluid. Phys. Fluids 21, 072105.CrossRefGoogle Scholar
Yu, Z. & Fan, L.-S. 2010 Multirelaxation-time interaction-potential-based lattice Boltzmann model for two-phase flow. Phys. Rev. E 82 (4), 046708.Google ScholarPubMed
Zhang, J., Liu, H. & Ba, Y. 2019 Numerical study of droplet dynamics on a solid surface with insoluble surfactants. Langmuir 35 (24), 7858–7870.CrossRefGoogle ScholarPubMed
Zhang, Z., Xu, S. & Ren, W. 2014 Derivation of a continuum model and the energy law for moving contact lines with insoluble surfactants. Phys. Fluids 26, 062103.CrossRefGoogle Scholar
Zhao, H., Zhang, W., Xu, J., Li, W. & Liu, H. 2017 Surfactant-laden drop jellyfish-breakup mode induced by the Marangoni effect. Exp. Fluids 58 (3), 13.CrossRefGoogle Scholar
Zinchenko, A. Z. & Davis, R. H. 2017 General rheology of highly concentrated emulsions with insoluble surfactant. J. Fluid Mech. 816, 661–704.CrossRefGoogle Scholar