Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-25T03:34:54.906Z Has data issue: false hasContentIssue false
  • English
  • Français

A model for the investigation of the second-order structure of caustic formations in dispersed flows

Published online by Cambridge University Press:  31 March 2020

Andreas Papoutsakis Open the ORCID record for Andreas Papoutsakis [Opens in a new window]  and
M. Gavaises
Andreas Papoutsakis*
Affiliation:
School of Mathematics, Computer Science and Engineering, Department of Mechanical Engineering and Aeronautics, City, University of London, London EC1V 0HB, UK
M. Gavaises
Affiliation:
School of Mathematics, Computer Science and Engineering, Department of Mechanical Engineering and Aeronautics, City, University of London, London EC1V 0HB, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

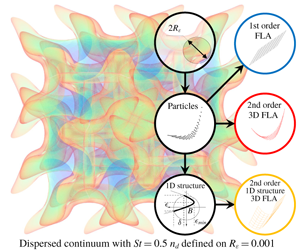
The formation of caustics by inertial particles is distinctive of dispersed flows. Their pressureless nature allows crossing trajectories resulting in singularities that cannot be captured accurately by standard Lagrangian approaches due to their fine spatial scale. A promising method for the investigation of caustics is the Osiptsov method or fully Lagrangian approach (FLA). The FLA has the advantage of identifying caustics, but its applicability is hindered by the occurrence of singularities. We present an original robust framework based on the FLA that provides an explicit expression of the dispersed phase structure that does not degenerate in the vicinity of caustics, using a single representative particle. The FLA is extended to account for the Hessian of the dispersed continuum (DC). It demonstrates the integrability of the FLA number density and allows for the calculation of the number density on a given length scale, retaining the functionality of the FLA. Number density models based on the second-order representation of the DC and on the one-dimensional structure of the particle distribution, that account for the anisotropy of the DC on caustics, are derived and applied for analytical flows. The number density is linked to a finite length scale, needed for the introduction of the FLA to spatially filtered flow fields. Finally, the method is used for the calculation of the interparticle separation on caustics. The identification of the structure of caustics presented in this work paves the way to a robust understanding of the mechanisms of particle accumulation.

JFM classification

Complex Fluids: Suspensions Drops and Bubbles: Aerosols/atomization
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 892 , 10 June 2020 , A4
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnold, V. I. 1992 Catastrophe Theory. Springer.CrossRefGoogle Scholar
Bec, J. 2003 Fractal clustering of inertial particles in random flows. Phys. Fluids 15 (11), L81–L84.CrossRefGoogle Scholar
Bell, M. L., Dominici, F., Ebisu, K., Zeger, S. L. & Samet, J. M. 2007 Spatial and temporal variation in pm2.5 chemical composition in the United States for health effects studies. Environ. Health Perspectives 115 (7), 989–995.CrossRefGoogle Scholar
Chen, L., Goto, S. & Vassilicos, J. C. 2006 Turbulent clustering of stagnation points and inertial particles. J. Fluid Mech. 553, 143–154.CrossRefGoogle Scholar
Crisanti, A., Falcioni, M., Provenzale, A., Tanga, P. & Vulpiani, A. 1992 Dynamics of passively advected impurities in simple two-dimensional flow models. Phys. Fluids A 4 (8), 1805–1820.CrossRefGoogle Scholar
Ducasse, L. & Pumir, A. 2009 Inertial particle collisions in turbulent synthetic flows: Quantifying the sling effect. Phys. Rev. E 80, 066312.Google ScholarPubMed
Fessler, J. R., Kulick, J. D. & Eaton, J. K. 1994 Preferential concentration of heavy particles in a turbulent channel flow. Phys. Fluids 6 (11), 3742–3749.CrossRefGoogle Scholar
Gustavsson, K. & Mehlig, B. 2016 Statistical models for spatial patterns of heavy particles in turbulence. Adv. Phys. 65 (1), 1–57.CrossRefGoogle Scholar
Gustavsson, K., Meneguz, E., Reeks, M. W. & Mehlig, B. 2012 Inertial-particle dynamics in turbulent flows: caustics, concentration fluctuations and random uncorrelated motion. New J. Phys. 14 (11), 115017.Google Scholar
Healy, D. P. & Young, J. B. 2005 Full Lagrangian methods for calculating particle concentration fields in dilute gas-particle flows. Proc. R. Soc. Lond A 461 (2059), 2197–2225.CrossRefGoogle Scholar
Ijzermans, R. H. A., Meneguz, E. & Reeks, M. W. 2010 Segregation of particles in incompressible random flows: singularities, intermittency and random uncorrelated motion. J. Fluid Mech. 653, 99–136.CrossRefGoogle Scholar
Ijzermans, R. H. A., Reeks, M. W., Meneguz, E., Picciotto, M. & Soldati, A. 2009 Measuring segregation of inertial particles in turbulence by a full Lagrangian approach. Phys. Rev. E 80, 015302.Google ScholarPubMed
Kasbaoui, M. H., Koch, D. L. & Desjardins, O. 2019 Clustering in Euler–Euler and Euler–Lagrange simulations of unbounded homogeneous particle-laden shear. J. Fluid Mech. 859, 174–203.CrossRefGoogle Scholar
Knight, G. 2012 Plastic Pollution. Heinemann Library.Google Scholar
Lebreton, L., Slat, B., Ferrari, F., Sainte-Rose, B., Aitken, J., Marthouse, R., Hajbane, S., Cunsolo, S., Schwarz, A., Levivier, A. et al. 2018 Evidence that the Great Pacific Garbage Patch is rapidly accumulating plastic. Sci. Rep. 8 (1), 4666.Google ScholarPubMed
Marble, F. E. 1970 Dynamics of dusty gases. Annu. Rev. Fluid Mech. 2 (1), 397–446.CrossRefGoogle Scholar
Marchioli, C. 2017 Large-eddy simulation of turbulent dispersed flows: a review of modelling approaches. Acta Mechanica 228 (3), 741–771.CrossRefGoogle Scholar
Meneguz, E. & Reeks, M. W. 2011 Statistical properties of particle segregation in homogeneous isotropic turbulence. J. Fluid Mech. 686, 338–351.CrossRefGoogle Scholar
Monchaux, R., Bourgoin, M. & Cartellier, A. 2012 Analyzing preferential concentration and clustering of inertial particles in turbulence. Intl J. Multiphase Flow 40, 1–18.CrossRefGoogle Scholar
Osiptsov, A. N. 1984 Investigation of regions of unbounded growth of the particle concentration in disperse flows. Fluid Dyn. 19 (3), 378–385.Google Scholar
Osiptsov, A. N. 2000 Lagrangian modelling of dust admixture in gas flows. Astrophys. Space Sci. 274, 377–386.CrossRefGoogle Scholar
Papoutsakis, A., Rybdylova, O. D., Zaripov, T. S., Danaila, L., Osiptsov, A. N. & Sazhin, S. S. 2018a Modelling of the evolution of a droplet cloud in a turbulent flow. Intl J. Multiphase Flow 104, 233–257.CrossRefGoogle Scholar
Papoutsakis, A., Sazhin, S. S., Begg, S., Danaila, I. & Luddens, F. 2018b An efficient adaptive mesh refinement (AMR) algorithm for the discontinuous galerkin method: applications for the computation of compressible two-phase flows. J. Comput. Phys. 363, 399–427.CrossRefGoogle Scholar
Picciotto, M., Marchioli, C., Reeks, M. W. & Soldati, A. 2005 Statistics of velocity and preferential accumulation of micro-particles in boundary layer turbulence. Nucl. Engng Des. 235 (10–12), 1239–1249.CrossRefGoogle Scholar
Pinsky, M. B. & Khain, A. P. 1997 Turbulence effects on droplet growth and size distribution in clouds – a review. J. Aerosol Sci. 28 (7), 1177–1214.CrossRefGoogle Scholar
Ravichandran, S. & Govindarajan, R. 2015 Caustics and clustering in the vicinity of a vortex. Phys. Fluids 27 (3), 033305.CrossRefGoogle Scholar
Rygg, A., Hindle, M. & Longest, P. W. 2016 Linking suspension nasal spray drug deposition patterns to pharmacokinetic profiles: a proof-of-concept study using computational fluid dynamics. J. Pharm. Sci. 105 (6), 1995–2004.CrossRefGoogle ScholarPubMed
Sazhin, S. S. 2014 Droplets and Sprays. Springer.CrossRefGoogle Scholar
Serrano, X. M., Baums, I. B., Smith, T. B., Jones, R. J., Shearer, T. L. & Baker, A. C. 2016 Long distance dispersal and vertical gene flow in the Caribbean brooding coral Porites astreoides. Sci. Rep. 6 (1), 21619.Google ScholarPubMed
Thomas, A. J. & Martin, J. M. 1986 First assessment of Chernobyl radioactive plume over Paris. Nature 321, 817–819.CrossRefGoogle ScholarPubMed
Tomita, K. & Den, M. 1986 Gauge-invariant perturbations in anisotropic homogeneous cosmological models. Phys. Rev. D 34 (12), 3570–3583.CrossRefGoogle ScholarPubMed
Vogel, S. 1994 Life in Moving Fluids: the Physical Biology of Flow. Princeton University Press.Google Scholar
Wilkinson, M. & Mehlig, B. 2005 Caustics in turbulent aerosols. Europhys. Lett. 71 (2), 186–192.CrossRefGoogle Scholar
Wilkinson, M., Mehlig, B., Östlund, S. & Duncan, K. P. 2007 Unmixing in random flows. Phys. Fluids 19 (11), 113303.CrossRefGoogle Scholar
Williams, F. A. 1958 Spray combustion and atomization. Phys. Fluids 1 (6), 541–545.CrossRefGoogle Scholar