Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-12-01T03:51:05.689Z Has data issue: false hasContentIssue false
  • English
  • Français

Modal instability of the flow in a toroidal pipe

Published online by Cambridge University Press:  08 March 2016

Jacopo Canton Open the ORCID record for Jacopo Canton [Opens in a new window] ,
Philipp Schlatter  and
Ramis Örlü
Jacopo Canton*
Affiliation:
Linné FLOW Centre, KTH Mechanics, Royal Institute of Technology, Stockholm, SE-100 44, Sweden Swedish e-Science Research Centre (SeRC), Royal Institute of Technology, Stockholm, SE-100 44, Sweden
Philipp Schlatter
Affiliation:
Linné FLOW Centre, KTH Mechanics, Royal Institute of Technology, Stockholm, SE-100 44, Sweden Swedish e-Science Research Centre (SeRC), Royal Institute of Technology, Stockholm, SE-100 44, Sweden
Ramis Örlü
Affiliation:
Linné FLOW Centre, KTH Mechanics, Royal Institute of Technology, Stockholm, SE-100 44, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The modal instability encountered by the incompressible flow inside a toroidal pipe is studied, for the first time, by means of linear stability analysis and direct numerical simulation (DNS). In addition to the unquestionable aesthetic appeal, the torus represents the smallest departure from the canonical straight pipe flow, at least for low curvatures. The flow is governed by only two parameters: the Reynolds number 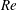$\mathit{Re}$ and the curvature of the torus 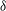${\it\delta}$, i.e. the ratio between pipe radius and torus radius. The absence of additional features, such as torsion in the case of a helical pipe, allows us to isolate the effect that the curvature has on the onset of the instability. Results show that the flow is linearly unstable for all curvatures investigated between 0.002 and unity, and undergoes a Hopf bifurcation at 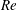$\mathit{Re}$ of about 4000. The bifurcation is followed by the onset of a periodic regime, characterised by travelling waves with wavelength 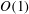$\mathit{O}(1)$ pipe diameters. The neutral curve associated with the instability is traced in parameter space by means of a novel continuation algorithm. Tracking the bifurcation provides a complete description of the modal onset of instability as a function of the two governing parameters, and allows a precise calculation of the critical values of 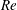$\mathit{Re}$ and 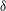${\it\delta}$. Several different modes are found, with differing properties and eigenfunction shapes. Some eigenmodes are observed to belong to groups with a set of common characteristics, deemed ‘families’, while others appear as ‘isolated’. Comparison with nonlinear DNS shows excellent agreement, confirming every aspect of the linear analysis, its accuracy, and proving its significance for the nonlinear flow. Experimental data from the literature are also shown to be in considerable agreement with the present results.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Instability: Instability Nonlinear Dynamical Systems: Nonlinear Dynamical Systems
Type
Papers
Information
Journal of Fluid Mechanics , Volume 792 , 10 April 2016 , pp. 894 - 909
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amestoy, R., Duff, I. & L’Excellent, J.-Y. 2000 Multifrontal parallel distributed symmetric and unsymmetric solvers. Comput. Meth. Appl. Math. 184, 501–520.Google Scholar
Berger, S. A., Talbot, L. & Yao, L. S. 1983 Flow in curved pipes. Annu. Rev. Fluid Mech. 15, 461–512.Google Scholar
Boussinesq, M. J. 1868 Mémoire sur l’influence des frottements dans les mouvements régulier des fluids. J. Math. Pure Appl. 13, 377–424.Google Scholar
Bulusu, K. V., Hussain, S. & Plesniak, M. W. 2014 Determination of secondary flow morphologies by wavelet analysis in a curved artery model with physiological inflow. Exp. Fluids 55, 1–20.Google Scholar
Canton, J.2013 Global linear stability of axisymmetric coaxial jets. Master’s thesis, Politecnico di Milano, https://www.politesi.polimi.it/handle/10589/87827.Google Scholar
Cioncolini, A. & Santini, L. 2006 An experimental investigation regarding the laminar to turbulent flow transition in helically coiled pipes. Exp. Therm. Fluid Sci. 30, 367–380.Google Scholar
Dean, W. R. 1927 Note on the motion of fluid in a curved pipe. Phil. Mag. 4, 208–223.Google Scholar
Dennis, S. C. R. 1980 Calculation of the steady flow through a curved tube using a new finite-difference method. J. Fluid Mech. 99, 449–467.CrossRefGoogle Scholar
Di Piazza, I. & Ciofalo, M. 2011 Transition to turbulence in toroidal pipes. J. Fluid Mech. 687, 72–117.Google Scholar
Eustice, J. 1910 Flow of water in curved pipes. Proc. R. Soc. Lond. A 84, 107–118.Google Scholar
Fischer, P. F., Lottes, J. W. & Kerkemeier, S. G.2008 nek5000 web page. http://nek5000.mcs.anl.gov.Google Scholar
Guckenheimer, J. & Holmes, P. 1983 Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer.Google Scholar
Hüttl, T. J. & Friedrich, R. 2001 Direct numerical simulation of turbulent flows in curved and helically coiled pipes. Comput. Fluids 30, 591–605.Google Scholar
Isachenko, V., Osipova, V. & Sukomel, A. 1974 Heat Transfer, 2nd edn. Mir Publishers.Google Scholar
Ito, H. 1959 Friction factors for turbulent flow in curved pipes. Trans. ASME J. Basic Engng 81, 123–134.Google Scholar
Ito, H. 1987 Flow in curved pipes. JSME Intl J. 30, 543–552.Google Scholar
Kühnen, J., Braunshier, P., Schwegel, M., Kuhlmann, H. C. & Hof, B. 2015 Subcritical versus supercritical transition to turbulence in curved pipes. J. Fluid Mech. 770, R3.Google Scholar
Kühnen, J., Holzner, M., Hof, B. & Kuhlmann, H. C. 2014 Experimental investigation of transitional flow in a toroidal pipe. J. Fluid Mech. 738, 463–491.Google Scholar
Lehoucq, R. B., Sorensen, D. C. & Yang, C. 1998 ARPACK Users Guide: Solution of Large-Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods. SIAM.Google Scholar
McConalogue, D. J. & Srivastava, R. S. 1968 Motion of a fluid in a curved tube. Proc. R. Soc. Lond. A 307, 37–53.Google Scholar
Noorani, A., El Khoury, G. K. & Schlatter, P. 2013 Evolution of turbulence characteristics from straight to curved pipes. Intl J. Heat Fluid Flow 41, 16–26.CrossRefGoogle Scholar
Noorani, A. & Schlatter, P. 2015 Evidence of sublaminar drag naturally occurring in a curved pipe. Phys. Fluids 27, 035105.Google Scholar
Salinger, A. G., Bou Rabee, N. M., Pawlowski, R. P., Wilkes, E. D., Borroughs, E. A., Lehoucq, R. B. & Romero, L. A.2002 LOCA, library of continuation algorithms: theory and implementation manual. SANDIA Report SAND2002-0396. Available at: http://prod.sandia.gov/techlib/access-control.cgi/2002/020396.pdf.Google Scholar
Schmid, P. J. & Henningson, D. S. 1994 Optimal energy density growth in Hagen–Poiseuille flow. J. Fluid Mech. 277, 197–225.Google Scholar
Sreenivasan, K. R. & Strykowski, P. J. 1983 Stabilization effects in flow through helically coiled pipes. Exp. Fluids 1 (1), 31–36.Google Scholar
Taylor, G. I. 1929 The criterion for turbulence in curved pipes. Proc. R. Soc. Lond. A 124, 243–249.Google Scholar
Van Dyke, M. 1978 Extended Stokes series: laminar flow through a loosely coiled pipe. J. Fluid Mech. 86, 129–145.Google Scholar
Vashisth, S., Kumar, V. & Nigam, K. D. P. 2008 A review on the potential applications of curved geometries in process industry. Ind. Engng Chem. Res. 47, 3291–3337.Google Scholar
Webster, D. R. & Humphrey, J. A. C. 1993 Experimental observations of flow instability in a helical coil (Data bank contribution). Trans. ASME J. Fluids Engng 115, 436–443.CrossRefGoogle Scholar
Webster, D. R. & Humphrey, J. A. C. 1997 Travelling wave instability in helical coil flow. Phys. Fluids 9, 407–418.Google Scholar
White, C. M. 1929 Streamline flow through curved pipes. Proc. R. Soc. Lond. A 123, 645–663.Google Scholar