Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-11T22:03:34.913Z Has data issue: false hasContentIssue false
  • English
  • Français

Modal and non-modal stability analysis of electrohydrodynamic flow with and without cross-flow

Published online by Cambridge University Press:  01 April 2015

Mengqi Zhang ,
Fulvio Martinelli ,
Jian Wu ,
Peter J. Schmid  and
Maurizio Quadrio
Mengqi Zhang*
Affiliation:
Département Fluides, Thermique, Combustion, Institut PPrime, CNRS-Université de Poitiers-ENSMA, UPR 3346, 43 Route de l’Aérodrome, Poitiers CEDEX F86036, France
Fulvio Martinelli
Affiliation:
Dipartimento di Scienze e Tecnologie Aerospaziali, Politecnico di Milano, via La Masa 34, 20156 Milano, Italy
Jian Wu
Affiliation:
Département Fluides, Thermique, Combustion, Institut PPrime, CNRS-Université de Poitiers-ENSMA, UPR 3346, 43 Route de l’Aérodrome, Poitiers CEDEX F86036, France
Peter J. Schmid
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK
Maurizio Quadrio
Affiliation:
Dipartimento di Scienze e Tecnologie Aerospaziali, Politecnico di Milano, via La Masa 34, 20156 Milano, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We report the results of a complete modal and non-modal linear stability analysis of the electrohydrodynamic flow for the problem of electroconvection in the strong-injection region. Convective cells are formed by the Coulomb force in an insulating liquid residing between two plane electrodes subject to unipolar injection. Besides pure electroconvection, we also consider the case where a cross-flow is present, generated by a streamwise pressure gradient, in the form of a laminar Poiseuille flow. The effect of charge diffusion, often neglected in previous linear stability analyses, is included in the present study and a transient growth analysis, rarely considered in electrohydrodynamics, is carried out. In the case without cross-flow, a non-zero charge diffusion leads to a lower linear stability threshold and thus to a more unstable flow. The transient growth, though enhanced by increasing charge diffusion, remains small and hence cannot fully account for the discrepancy of the linear stability threshold between theoretical and experimental results. When a cross-flow is present, increasing the strength of the electric field in the high-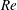$\mathit{Re}$ Poiseuille flow yields a more unstable flow in both modal and non-modal stability analyses. Even though the energy analysis and the input–output analysis both indicate that the energy growth directly related to the electric field is small, the electric effect enhances the lift-up mechanism. The symmetry of channel flow with respect to the centreline is broken due to the additional electric field acting in the wall-normal direction. As a result, the centres of the streamwise rolls are shifted towards the injector electrode, and the optimal spanwise wavenumber achieving maximum transient energy growth increases with the strength of the electric field.

JFM classification

Instability: Instability MHD and Electrohydrodynamics: MHD and Electrohydrodynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 770 , 10 May 2015 , pp. 319 - 349
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alj, A., Denat, A., Gosse, J.-P., Gosse, B. & Nakamura, I. 1985 Creation of charge carriers in nonpolar liquids. IEEE Trans. Elec. Insul. 20 (2), 221–231.Google Scholar
Allen, P. & Karayiannis, T. 1995 Electrohydrodynamic enhancement of heat transfer and fluid flows. Heat Recov. Syst. CHP 15 (5), 389–423.CrossRefGoogle Scholar
Atten, P. 1974 Electrohydrodynamic stability of dielectric liquids during transient regime of space-charge-limited injection. Phys. Fluids 17 (10), 1822–1827.Google Scholar
Atten, P. 1976 Rôle de la diffusion dans le problème de la stabilité hydrodynamique d’un liquide dièlectrique soumis à une injection unipolaire forte. C. R. Acad. Sci. Paris 283, 29–32.Google Scholar
Atten, P. & Honda, T. 1982 The electroviscous effect and its explanation I – The electrohydrodynamic origin; study under unipolar D.C. injection. J. Electrostat. 11 (3), 225–245.Google Scholar
Atten, P. & Lacroix, J. C. 1979 Non-linear hydrodynamic stability of liquids subjected to unipolar injection. J. Méc. 18, 469–510.Google Scholar
Atten, P. & Moreau, R. 1972 Stabilité electrohydrodynamique des liquides isolants soumis à une injection unipolaire. J. Méc. 11, 471–520.Google Scholar
Bart, S. F., Tavrow, L. S., Mehregany, M. & Lang, J. H. 1990 Microfabricated electrohydrodynamic pumps. Sensors Actuators A 21 (1–3), 193–197.CrossRefGoogle Scholar
Boyd, J. 2001 Chebyshev and Fourier Spectral Methods, 2nd revised edn. Dover.Google Scholar
Bradshaw, P. 1969 The analogy between streamline curvature and buoyancy in turbulent shear flow. J. Fluid Mech. 36, 177–191.Google Scholar
Brandt, L. 2014 The lift-up effect: the linear mechanism behind transition and turbulence in shear flows. Eur. J. Mech. (B/Fluids) 47, 80–96.CrossRefGoogle Scholar
Bushnell, D. M. & McGinley, C. B. 1989 Turbulence control in wall flows. Annu. Rev. Fluid Mech. 21, 1–20.CrossRefGoogle Scholar
Butler, K. M. & Farrell, B. F. 1992 Three-dimensional optimal perturbations in viscous shear flow. Phys. Fluids 4 (8), 1637–1650.Google Scholar
Butler, K. M. & Farrell, B. F. 1993 Optimal perturbations and streak spacing in wall-bounded turbulent shear flows. Phys. Fluids A 5 (3), 774–777.CrossRefGoogle Scholar
Castellanos, A. 1998 Electrohydrodynamics. Springer.Google Scholar
Castellanos, A. & Agrait, N. 1992 Unipolar injection induced instabilities in plane parallel flows. IEEE Trans. Ind. Applics. 28 (3), 513–519.CrossRefGoogle Scholar
Chakraborty, S., Liao, I.-C., Adler, A. & Leong, K. W. 2009 Electrohydrodynamics: a facile technique to fabricate drug delivery systems. Adv. Drug Deliv. Rev. 61 (12), 1043–1054.Google Scholar
Darabi, J., Rada, M., Ohadi, M. & Lawler, J. 2002 Design, fabrication, and testing of an electrohydrodynamic ion-drag micropump. J. Microelectromech. Syst. 11 (6), 684–690.Google Scholar
Dubief, Y., White, C. M., Terrapon, V. E., Shaqfeh, E. S. G., Moin, P. & Lele, S. K. 2004 On the coherent drag-reducing and turbulence-enhancing behaviour of polymers in wall flows. J. Fluid Mech. 514, 271–280.CrossRefGoogle Scholar
Farrell, B. F. & Ioannou, P. J. 1996 Generalized stability theory. Part I: autonomous operators. J. Atmos. Sci. 53 (14), 2025–2040.Google Scholar
Félici, N. 1971 DC conduction in liquid dielectrics (Part II): electrohydrodynamic phenomena. Direct Curr. Power Electron. 2, 147–165.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Harten, A. 1983 High resolution schemes for hyperbolic conservation laws. J. Comput. Phys. 49 (3), 357–393.Google Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.Google Scholar
Jones, T. 1978 Electrohydrodynamically enhanced heat transfer in liquids – a review. Adv. Heat Transfer 14, 107–148.Google Scholar
Jovanović, M. R. & Bamieh, B. 2005 Componentwise energy amplification in channel flows. J. Fluid Mech. 534, 145–183.CrossRefGoogle Scholar
Kim, J. 2003 Control of turbulent boundary layers. Phys. Fluids 15 (5), 1093–1105.CrossRefGoogle Scholar
Kim, J. & Bewley, T. R. 2007 A linear systems approach to flow control. Annu. Rev. Fluid Mech. 39 (1), 383–417.CrossRefGoogle Scholar
Kourmatzis, A. & Shrimpton, J. S. 2012 Turbulent three-dimensional dielectric electrohydrodynamic convection between two plates. J. Fluid Mech. 696, 228–262.CrossRefGoogle Scholar
Lacroix, J. C., Atten, P. & Hopfinger, E. J. 1975 Electro-convection in a dielectric liquid layer subjected to unipolar injection. J. Fluid Mech. 69, 539–563.CrossRefGoogle Scholar
Landahl, M. T. 1980 A note on an algebraic instability of inviscid parallel shear flows. J. Fluid Mech. 98, 243–251.Google Scholar
Lee, J.-G., Cho, H.-J., Huh, N., Ko, C., Lee, W.-C., Jang, Y.-H., Lee, B. S., Kang, I. S. & Choi, J.-W. 2006 Electrohydrodynamic (EHD) dispensing of nanoliter DNA droplets for microarrays. Biosens. Bioelectr. 21 (12), 2240–2247.Google Scholar
Martinelli, F., Quadrio, M. & Schmid, P. J.2011 Stability of planar shear flow in presence of electroconvection. In Proceedings of the Seventh International Symposium on Turbulence and Shear Flow Phenomena (TSFP-7), July 2011, Ottawa, Canada.Google Scholar
Melcher, J. R. 1981 Continuum Electromechanics. MIT Press.Google Scholar
Ogilvie, G. I. & Proctor, M. R. E. 2003 On the relation between viscoelastic and magnetohydrodynamic flows and their instabilities. J. Fluid Mech. 476, 389–409.Google Scholar
Pérez, A. T. & Castellanos, A. 1989 Role of charge diffusion in finite-amplitude electroconvection. Phys. Rev. A 40, 5844–5855.Google Scholar
Saad, Y. 2011 Numerical Methods for Large Eigenvalue Problems. SIAM.CrossRefGoogle Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.CrossRefGoogle Scholar
Schmid, P. J. & Brandt, L. 2014 Analysis of fluid systems: stability, receptivity, sensitivity. Appl. Mech. Rev. 66 (2), 024803.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Schneider, J. M. & Watson, P. K. 1970 Electrohydrodynamic stability of space-charge-limited currents in dielectric liquids. I. Theoretical study. Phys. Fluids 13 (8), 1948–1954.CrossRefGoogle Scholar
Schoppa, W. & Hussain, F. 1998 A large-scale control strategy for drag reduction in turbulent boundary layers. Phys. Fluids 10 (5), 1049–1051.Google Scholar
Soldati, A. & Banerjee, S. 1998 Turbulence modification by large-scale organized electrohydrodynamic flows. Phys. Fluids 10 (7), 1742–1756.Google Scholar
Traoré, P. H. & Pérez, A. T. 2012 Two-dimensional numerical analysis of electroconvection in a dielectric liquid subjected to strong unipolar injection. Phys. Fluids 24 (3), 037102.Google Scholar
Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscoll, T. A. 1993 Hydrodynamic stability without eigenvalues. Science 261 (5121), 578–584.CrossRefGoogle ScholarPubMed
Weideman, J. A. & Reddy, S. C. 2000 A MATLAB differentiation matrix suite. ACM Trans. Math. Softw. 26 (4), 465–519.Google Scholar
Wu, J., Traoré, P., Vázquez, P. A. & Pérez, A. T. 2013 Onset of convection in a finite two-dimensional container due to unipolar injection of ions. Phys. Rev. E 88, 053018.Google Scholar
Zhang, M., Lashgari, I., Zaki, T. A. & Brandt, L. 2013 Linear stability analysis of channel flow of viscoelastic Oldroyd-B and FENE-P fluids. J. Fluid Mech. 737, 249–279.Google Scholar