Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-25T16:57:27.708Z Has data issue: false hasContentIssue false
  • English
  • Français

Mixing in axisymmetric gravity currents

Published online by Cambridge University Press:  06 October 2015

Peeradon Samasiri  and
Andrew W. Woods
Peeradon Samasiri
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
Andrew W. Woods*
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present new experiments to measure the rate of entrainment of ambient fluid into a high Reynolds number, axisymmetric, turbulent gravity current. The current is produced by the rapid release of a finite volume of aqueous salt solution from a lock of length 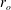$r_{o}$ into a diverging channel, 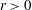$r>0$, of angle 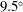$9.5^{\circ }$, filled with a finite depth, 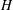$H$, of fresh water. Using light attenuation we measure the evolving density of the flow, and using dye studies we illustrate the process of mixing between the current and ambient fluid. After an initial adjustment, a circulation develops in the head of the flow: current fluid reaches the nose of the flow, rises up and moves backwards relative to the nose. We find that, owing to the mixing, the volume of the current increases as 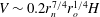$V\sim 0.2r_{n}^{7/4}r_{o}^{1/4}H$ while the maximum depth of the head decreases as 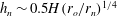$h_{n}\sim 0.5H(r_{o}/r_{n})^{1/4}$, where 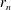$r_{n}$ is the location of the front of the current. Combining these results, we estimate that the recirculating current fluid mixes with a fraction 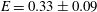$E=0.33\pm 0.09$ of the ambient fluid that is directly ahead of the current and displaced upwards by it. Some of the mixed fluid supplies the tail of the flow, while the remainder recirculates into the head, which becomes progressively more dilute. In accord with Huppert & Simpson (J. Fluid Mech., vol. 99, 1980, pp. 785–799), we find that the position of the front increases with time as 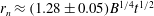$r_{n}\approx (1.28\pm 0.05)B^{1/4}t^{1/2}$, where 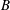$B$ is the total buoyancy of the flow. We also find that the maximum value of the vertical integral of the buoyancy 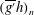$(\overline{g^{\prime }}h)_{n}$ decreases with the position of the nose according to the relation 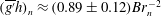$(\overline{g^{\prime }}h)_{n}\approx (0.89\pm 0.12)Br_{n}^{-2}$, consistent with a Froude number 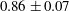$0.86\pm 0.07$. We compare our measurements with a new idealised self-similar solution of the depth-averaged equations that accounts for the mixing at the nose, the vertical shear in the velocity and the lateral stratification of the buoyancy within the current.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Gravity currents
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 782 , 10 November 2015 , R1
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adduce, C., Sciortino, G. & Proietti, S. 2012 Gravity currents produced by lock exchanges: experiments and simulations with a two-layer shallow-water model with entrainment. J. Hydraul. Engng 138 (2), 111–121.Google Scholar
Benjamin, T. B. 1968 Gravity currents and related phenomena. J. Fluid Mech. 31 (02), 209–248.Google Scholar
Bonnecaze, R. T., Hallworth, M. A., Huppert, H. E. & Lister, J. R. 1995 Axisymmetric particle-driven gravity currents. J. Fluid Mech. 294, 93–121.Google Scholar
Cantero, M. I., Balachandar, S. & Garcia, M. H. 2007a High-resolution simulations of cylindrical density currents. J. Fluid Mech. 590, 437–469.Google Scholar
Cantero, M. I., Lee, J. R., Balachandar, S. & Garcia, M. H. 2007b On the front velocity of gravity currents. J. Fluid Mech. 586, 1–39.Google Scholar
Chen, J.-C.1980 Studies on gravitational spreading currents. PhD thesis, California Institute of Technology.Google Scholar
Fragoso, A. T., Patterson, M. D. & Wettlaufer, J. S. 2013 Mixing in gravity currents. J. Fluid Mech. 734, R2.Google Scholar
Hacker, J., Linden, P. F. & Dalziel, S. B. 1996 Mixing in lock-release gravity currents. Dyn. Atmos. Oceans 24 (1–4), 183–195.Google Scholar
Hallworth, M. A., Huppert, H. E., Phillips, J. C. & Sparks, R. S. J. 1996 Entrainment into two-dimensional and axisymmetric turbulent gravity currents. J. Fluid Mech. 308, 289–311.Google Scholar
Hallworth, M. A., Phillips, J. C., Huppert, H. E. & Sparks, R. S. J. 1993 Entrainment in turbulent gravity currents. Nature 362, 829–831.Google Scholar
Huppert, H. E. & Simpson, J. E. 1980 The slumping of gravity currents. J. Fluid Mech. 99 (04), 785–799.Google Scholar
Johnson, C. G. & Hogg, A. J. 2013 Entraining gravity currents. J. Fluid Mech. 731, 477–508.Google Scholar
Kneller, B. & Buckee, C. 2000 The structure and fluid mechanics of turbidity currents: a review of some recent studies and their geological implications. Sedimentology 47, 62–94.Google Scholar
Özgökmen, T. M., Iliescu, T. & Fischer, P. F. 2009 Reynolds number dependence of mixing in a lock-exchange system from direct numerical and large eddy simulations. Ocean Model. 30 (2–3), 190–206.Google Scholar
Patterson, M. D., Simpson, J. E., Dalziel, S. B. & van Heijst, G. F. 2006 Vortical motion in the head of an axisymmetric gravity current. Phys. Fluids 18 (4), 046601.Google Scholar
Prandtl, L. 1952 Essentials of Fluid Dynamics: With Applications to Hydraulics Aeronautics, Meteorology, and Other Subjects. Hafner.Google Scholar
Sher, D. & Woods, A. W. 2015 Gravity currents: entrainment, stratification and self-similarity. J. Fluid Mech. (in press).Google Scholar
Simpson, J. E. 1999 Gravity Currents: In the Environment and the Laboratory. Cambridge University Press.Google Scholar
Slim, A. C. & Huppert, H. E. 2004 Self-similar solutions of the axisymmetric shallow-water equations governing converging inviscid gravity currents. J. Fluid Mech. 506, 331–355.Google Scholar
van Sommeren, D. D. J. A., Caulfield, C. P. & Woods, A. W. 2012 Turbulent buoyant convection from a maintained source of buoyancy in a narrow vertical tank. J. Fluid Mech. 701, 278–303.Google Scholar
Sparks, R. S. J., Bursik, M. I., Carey, S. N., Gilbert, J., Glaze, L. S., Sigurdsson, H. & Woods, A. 1997 Volcanic Plumes. Wiley.Google Scholar
Turner, J. S. 1979 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar