Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T10:32:29.276Z Has data issue: false hasContentIssue false
  • English
  • Français

Mixing in a sheared particulate suspension

Published online by Cambridge University Press:  20 April 2021

Régis Turuban ,
Henri Lhuissier Open the ORCID record for Henri Lhuissier [Opens in a new window]  and
Bloen Metzger Open the ORCID record for Bloen Metzger [Opens in a new window]
Régis Turuban
Affiliation:
Aix Marseille Univ, CNRS, Institut Universitaire des Systèmes Thermiques et Industriels, 13453 Marseille, France
Henri Lhuissier
Affiliation:
Aix Marseille Univ, CNRS, Institut Universitaire des Systèmes Thermiques et Industriels, 13453 Marseille, France
Bloen Metzger*
Affiliation:
Aix Marseille Univ, CNRS, Institut Universitaire des Systèmes Thermiques et Industriels, 13453 Marseille, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

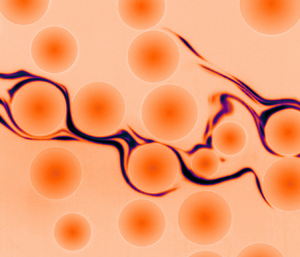
In a sheared suspension, the chaotic motion of the particles disperses the suspending liquid and drives an exponential and broadly distributed growth of the elongation of its material lines. This paper addresses experimentally and theoretically the consequences of this complex advection on the mixing of an initially segregated blob of diffusive dye, at large Péclet number and down to the finest scales of mixing. As the suspension is sheared, the combined action of the mean and fluctuating components of the flow stretches and folds the blob into a multi-scale lamellar structure. At short time, overlaps between the lamellae are scarce and the probability distribution concentration can be understood from the local stretching statistics only. At intermediate times, dispersion limits the volume within which lamellae deploy; overlaps become abundant and their statistics determine the concentration distribution. At longer times, the dye becomes homogeneous at the particle scale and the concentration distribution is set by dispersion only. Predictions for both the concentration distribution and the transitions between these successive stages of mixing are provided and compared to the experimental results.

JFM classification

Complex Fluids: Suspensions Mixing: Chaotic advection Mixing: Laminar mixing
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 916 , 10 June 2021 , R4
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Berg, M., Davit, Y., Quintard, M. & Lorthois, S. 2020 Modelling solute transport in the brain microcirculation: is it really well mixed inside the blood vessels? J. Fluid Mech. 884, A39.CrossRefGoogle Scholar
Dbouk, T. 2018 Heat transfer and shear-induced migration in dense non-Brownian suspension flows: modelling and simulation. J. Fluid Mech. 840, 432.CrossRefGoogle Scholar
Duplat, J., Innocenti, C. & Villermaux, E. 2010 A nonsequential turbulent mixing process. Phys. Fluids 22, 035104.CrossRefGoogle Scholar
Goldstein, R.E. & van de Meent, J.-E. 2015 A physical perspective on cytoplasmic streaming. Interface Focus 5, 20150030.CrossRefGoogle ScholarPubMed
Kabacaoğlu, G., Quaife, B. & Biros, G. 2017 Quantification of mixing in vesicle suspensions using numerical simulations in two dimensions. Phys. Fluids 29 (2), 021901.CrossRefGoogle ScholarPubMed
Kaoui, B. 2018 Computer simulations of drug release from a liposome into the bloodstream. Eur. Phys. J. E 41 (2), 1–6.CrossRefGoogle ScholarPubMed
Le Borgne, T., Dentz, M. & Villermaux, E. 2015 The lamellar description of mixing in porous media. J. Fluid Mech. 770, 458–498.CrossRefGoogle Scholar
Metzger, B., Rahli, O. & Yin, X. 2013 Heat transfer across sheared suspensions: role of the shear-induced diffusion. J. Fluid Mech. 724, 527–552.CrossRefGoogle Scholar
Meunier, P. & Villermaux, E. 2003 How vortices mix. J. Fluid Mech. 476, 213–222.CrossRefGoogle Scholar
Ranz, W.E. 1979 Applications of a stretch model to mixing, diffusion, and reaction in laminar and turbulent flows. AIChE J. 25, 41–47.CrossRefGoogle Scholar
Rhines, P.B. & Young, W.R. 1983 How rapidly is a passive scalar mixed within closed streamlines? J. Fluid Mech. 133, 133–145.CrossRefGoogle Scholar
Sierou, A. & Brady, J.F. 2004 Shear-induced self-diffusion in non-colloidal suspensions. J. Fluid Mech. 506, 285–314.CrossRefGoogle Scholar
Smoluchowski, M.V. 1917 Versuch einer mathematischen theorie der koagulationskinetik kolloider losungen. Z. Phys. Chem. 92, 129–168.Google Scholar
Souzy, M., Lhuissier, H., Villermaux, E. & Metzger, B. 2017 Stretching and mixing in sheared particulate suspensions. J. Fluid Mech. 812, 611–635.CrossRefGoogle Scholar
Souzy, M., Yin, X., Villermaux, E., Abid, C. & Metzger, B. 2015 Super-diffusion in sheared suspensions. Phys. Fluids 27, 041705.CrossRefGoogle Scholar
Souzy, M., Zaier, I., Lhuissier, H., Le Borgne, T. & Metzger, B. 2018 Mixing lamellae in a shear flow. J. Fluid Mech. 838, R3.CrossRefGoogle Scholar
Thøgersen, K. & Dabrowski, M. 2017 Mixing of the fluid phase in slowly sheared particle suspensions of cylinders. J. Fluid Mech. 818, 807.CrossRefGoogle Scholar
Villermaux, E. 2019 Mixing versus stirring. Annu. Rev. Fluid Mech. 51, 245–273.CrossRefGoogle Scholar
Yousefi, A., Ardekani, M.N., Picano, F. & Brandt, L. 2020 Regimes of heat transfer in particle suspensions. arXiv:2007.07006.Google Scholar

Turuban et al. supplementary movie

Mixing of a blob of diffusive dye in a sheared particulate suspension at low and large Péclet number.

Download Turuban et al. supplementary movie(Video)
Video 35.2 MB