Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-30T17:06:21.612Z Has data issue: false hasContentIssue false
  • English
  • Français

Mixing efficiency in large-eddy simulations of stratified turbulence

Published online by Cambridge University Press:  18 June 2018

Sina Khani Open the ORCID record for Sina Khani [Opens in a new window]
Sina Khani*
Affiliation:
Program in Atmospheric and Oceanic Sciences, Princeton University, Princeton, NJ 08544, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The irreversible mixing efficiency is studied using large-eddy simulations (LES) of stratified turbulence, where three different subgrid-scale (SGS) parameterizations are employed. For comparison, direct numerical simulations (DNS) and hyperviscosity simulations are also performed. In the regime of stratified turbulence where $Fr_{v}\sim 1$, the irreversible mixing efficiency 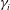$\unicode[STIX]{x1D6FE}_{i}$ in LES scales like 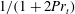$1/(1+2Pr_{t})$, where 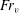$Fr_{v}$ and 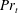$Pr_{t}$ are the vertical Froude number and turbulent Prandtl number, respectively. Assuming a unit scaling coefficient and 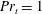$Pr_{t}=1$, 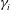$\unicode[STIX]{x1D6FE}_{i}$ goes to a constant value 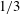$1/3$, in agreement with DNS results. In addition, our results show that the irreversible mixing efficiency in LES, while consistent with this prediction, depends on SGS parameterizations and the grid spacing 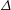$\unicode[STIX]{x1D6E5}$. Overall, the LES approach can reproduce mixing efficiency results similar to those from the DNS approach if 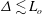$\unicode[STIX]{x1D6E5}\lesssim L_{o}$, where 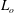$L_{o}$ is the Ozmidov scale. In this situation, the computational costs of numerical simulations are significantly reduced because LES runs require much smaller computational resources in comparison with expensive DNS runs.

JFM classification

Turbulent Flows: Stratified turbulence Mixing: Turbulent mixing Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 849 , 25 August 2018 , pp. 373 - 394
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Armenio, V. & Sarkar, S. 2002 An investigation of stably stratified turbulent channel flow using large-eddy simulation. J. Fluid Mech. 459, 1–42.Google Scholar
Bartello, P. & Tobias, S. M. 2013 Sensitivity of stratified turbulence to the buoyancy Reynolds number. J. Fluid Mech. 725, 1–22.Google Scholar
Billant, P. & Chomaz, J.-M. 2001 Self-similarity of strongly stratified inviscid flows. Phys. Fluids 13 (6), 1645–1651.Google Scholar
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J.-M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.Google Scholar
Caulfield, C. P. & Peltier, W. R. 2000 The anatomy of the mixing transition in homogeneous and stratified free shear layers. J. Fluid Mech. 413, 1–47.Google Scholar
Elliott, Z. A. & Venayagamoorthy, S. K. 2011 Evaluation of turbulent Prandtl (Schmidt) number parameterizations for stably stratified environmental flows. Dyn. Atmos. Oceans 51, 137–150.Google Scholar
Germano, M., Piomelli, U., Moin, P. & Cabot, W. H. 1991 A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A 3 (7), 1760–1765.Google Scholar
Kaltenback, H.-J., Gerz, T. & Schumann, U. 1994 Large-eddy simulation of homogeneous turbulence and diffusion in stably stratified shear flow. J. Fluid Mech. 280, 1–40.Google Scholar
Khani, S.2015 Large eddy simulations and subgrid scale motions in stratified turbulence. PhD Thesis, University of Waterloo; UWSpace http://hdl.handle.net/10012/9209.Google Scholar
Khani, S. & Porté-Agel, F. 2017 Evaluation of non-eddy viscosity subgrid-scale models in stratified turbulence using direct numerical simulations. Eur. J. Mech. (B/Fluids) 65, 168–178.Google Scholar
Khani, S. & Waite, M. L. 2013 Effective eddy viscosity in stratified turbulence. J. Turbul. 14 (7), 49–70.Google Scholar
Khani, S. & Waite, M. L. 2014 Buoyancy scale effects in large-eddy simulations of stratified turbulence. J. Fluid Mech. 754, 75–97.Google Scholar
Khani, S. & Waite, M. L. 2015 Large eddy simulations of stratified turbulence: the dynamic Smagorinsky model. J. Fluid Mech. 773, 327–344.Google Scholar
Khani, S. & Waite, M. L. 2016 Backscatter in stratified turbulence. Eur. J. Mech. (B/Fluids) 60, 1–12.Google Scholar
Kraichnan, R. H. 1976 Eddy viscosity in two and three dimensions. J. Atmos. Sci. 33, 1521–1536.Google Scholar
Lilly, D. K. 1967 The representation of small-scale turbulence in numerical simulation experiments. In NCAR Manuscript, vol. 281, pp. 99–164. National Center for Atmospheric Research.Google Scholar
Lilly, D. K., Waco, D. E. & Adelfang, S. I. 1974 Stratospheric mixing estimated from high-altitude turbulence measurements. J. Appl. Meteor. 13, 488–493.Google Scholar
Lindborg, E. 2006 The energy cascade in strongly stratified fluid. J. Fluid Mech. 550, 207–242.Google Scholar
Lindborg, E. & Cho, J. Y. N. 2001 Horizontal velocity structure functions in the upper troposphere and lower stratosphere. 2. Theoretical considerations. J. Geophys. Res. 106 (10), 10233–10241.Google Scholar
Maffioli, A., Brethouwer, G. & Lindborg, E. 2016 Mixing efficiency in stratified turbulence. J. Fluid Mech. 794, R3.Google Scholar
Mashayek, A., Salehipour, H., Bouffard, D., Caulfield, C. P., Ferrari, R., Nikurashin, M., Pletier, W. R. & Smyth, W. D. 2017 Efficiency of turbulent mixing in the abyssal ocean circulation. Geophys. Res. Lett. 44 (12), 6296–6306.Google Scholar
Métais, O. & Lesieur, M. S. 1992 Spectral large-eddy simulation of isotropic and stably stratified turbulence. J. Fluid Mech. 239, 3157–3194.Google Scholar
Moin, P. & Mahesh, K. 1998 Direct numerical simulation: a tool in turbulence research. Annu. Rev. Fluid Mech. 30, 539–578.Google Scholar
Nastrom, G. D. & Gage, K. S. 1985 A climatology of atmospheric wavenumber spectra observed by commercial aircraft. J. Atmos. Sci. 42, 950–960.Google Scholar
Orszag, S. A. 1971 On the elimination of aliasing in finite-difference schemes by filtering high-wavenumber components. J. Atmos. Sci. 28, 1074–1074.Google Scholar
Osborn, T. R. 1980 Estimates of the local rate of vertical diffusion from dissipation measurements. J. Phys. Oceanogr. 10, 83–89.Google Scholar
Pardyjak, E. R., Monti, P. & Fernando, H. J. S. 2002 Flux Richardson number measurements in stable atmospheric shear flows. J. Fluid Mech. 459, 307–316.Google Scholar
Peltier, W. R. & Caulfield, C. P. 2003 Mixing efficiency is stratified shear flows. Annu. Rev. Fluid Mech. 35, 135–167.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Porté-Agel, F., Meneveau, C. & Parlange, M. B. 2000 A scale-dependent dynamic model for large-eddy simulation: application to a neutral atmospheric boundary layer. J. Fluid Mech. 415, 261–284.Google Scholar
Remmler, S. & Hickel, S. 2012 Direct and large eddy simulation of stratified turbulence. Intl J. Heat Fluid Flow 35, 13–24.Google Scholar
Remmler, S. & Hickel, S. 2014 Spectral eddy viscosity of stratified turbulence. J. Fluid Mech. 755, R6.Google Scholar
Riley, J. J. & M.-P, Lelong 2000 Fluid motions in the presence of strong stable stratification. Annu. Rev. Fluid Mech. 32, 613–657.Google Scholar
Riley, J. J. & Lindborg, E. 2008 Stratified turbulence: a possible interpretation of some geophysical turbulence measurements. J. Atmos. Sci. 65, 2416–2424.Google Scholar
Salehipour, H. & Peltier, W. R. 2015 Diapycnal diffusivity, turbulent Prandtl number and mixing efficiency in Boussinesq stratified turbulence. J. Fluid Mech. 775, 464–500.Google Scholar
Schaefer-Rolffs, U. 2016 A generalized formulation of the dynamic Smagorinsky model. Meteorol. Z. 26 (2), 181–187.Google Scholar
Shih, L. H., Koseff, J. R., Ivey, G. N. & Ferziger, J. H. 2005 Parameterizations of turbulent fluxes and scales using homogeneous sheared stably stratified turbulence simulations. J. Fluid Mech. 525, 193–214.Google Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equations. I. The basic experiment. Mon. Weath. Rev. 91 (3), 99–164.Google Scholar
Strang, E. J. & Fernando, H. J. S. 2001 Entrainment and mixing in stratified shear flows. J. Fluid Mech. 428, 349–386.Google Scholar
Venayagamoorthy, S. K. & Stretch, D. D. 2010 On the turbulent Prandtl number in homogeneous stably stratified turbulence. J. Fluid Mech. 644, 359–369.Google Scholar
Waite, M. L. 2014 Direct numerical simulations of laboratory-scale stratified turbulence. In Modeling Atmospheric and Oceanic Flows: Insights from Laboratory Experiments (ed. von Larcher, T. & Williams, P.), pp. 159–175. American Geophys. Union.Google Scholar
Waite, M. L. 2011 Stratified turbulence at the buoyancy scale. Phys. Fluids 23, 066602.Google Scholar
Waite, M. L. & Bartello, P. 2004 Stratified turbulence dominated by vortical motion. J. Fluid Mech. 517, 281–303.Google Scholar
Weinstock, J. 1978 Vertical turbulent diffusion in a stably stratified fluid. J. Atmos. Sci. 35, 1022–1027.Google Scholar