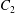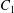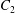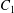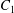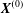1 Introduction
The hydrodynamics of pairwise interaction of deformable particles is a crucial topic for semi-dilute suspension rheology (Batchelor & Green Reference Batchelor and Green1972a; Guazzelli & Morris Reference Guazzelli and Morris2012). When the particles are deformable, their shear induced deformation leads to non-Newtonian and to self-diffusion effects. This has been demonstrated for liquid droplets (Loewenberg & Hinch Reference Loewenberg and Hinch1997; Guido & Simeone Reference Guido and Simeone1998). The case of capsules (liquid drop enclosed by a thin elastic membrane) is particularly complex because the motion and deformation of those particles result from nonlinear fluid–structure interactions that are difficult to model. For example, the capsules may be highly deformed as they cross each other, which leads to the formation of a thin liquid film between the two particles and to potential damage of the membrane due to high shearing forces.
This phenomenon is usually studied in a simple shear flow with velocity components given by 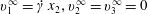 $v_{1}^{\infty }=\dot{\unicode[STIX]{x1D6FE}}\,x_{2},v_{2}^{\infty }=v_{3}^{\infty }=0$ in a laboratory Cartesian reference frame, where
$v_{1}^{\infty }=\dot{\unicode[STIX]{x1D6FE}}\,x_{2},v_{2}^{\infty }=v_{3}^{\infty }=0$ in a laboratory Cartesian reference frame, where 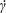 $\dot{\unicode[STIX]{x1D6FE}}$ is the shear rate. The two capsules
$\dot{\unicode[STIX]{x1D6FE}}$ is the shear rate. The two capsules 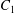 $C_{1}$ and
$C_{1}$ and 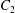 $C_{2}$ are initially positioned with distances
$C_{2}$ are initially positioned with distances  $\unicode[STIX]{x0394}X_{1}^{(0)},\unicode[STIX]{x0394}X_{2}^{(0)},\unicode[STIX]{x0394}X_{3}^{(0)}$ between their centres. The first three-dimensional model of two initially spherical identical capsules (radius
$\unicode[STIX]{x0394}X_{1}^{(0)},\unicode[STIX]{x0394}X_{2}^{(0)},\unicode[STIX]{x0394}X_{3}^{(0)}$ between their centres. The first three-dimensional model of two initially spherical identical capsules (radius  $a$) interacting in simple shear flow is due to Lac, Morel & Barthès-Biesel (Reference Lac, Morel and Barthès-Biesel2007), who considered the case where the two capsules had their centres in the same
$a$) interacting in simple shear flow is due to Lac, Morel & Barthès-Biesel (Reference Lac, Morel and Barthès-Biesel2007), who considered the case where the two capsules had their centres in the same 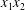 $x_{1}x_{2}$ shear plane (
$x_{1}x_{2}$ shear plane (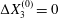 $\unicode[STIX]{x0394}X_{3}^{(0)}=0$). The capsule membrane is treated as a very thin sheet of a hyperelastic material devoid of bending resistance and the flow Reynolds number is assumed to be negligible. Lac et al. showed that, in a reference frame centred on
$\unicode[STIX]{x0394}X_{3}^{(0)}=0$). The capsule membrane is treated as a very thin sheet of a hyperelastic material devoid of bending resistance and the flow Reynolds number is assumed to be negligible. Lac et al. showed that, in a reference frame centred on 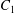 $C_{1}$, capsule
$C_{1}$, capsule 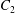 $C_{2}$ is first displaced along the velocity gradient so that it can overpass (‘jump over’)
$C_{2}$ is first displaced along the velocity gradient so that it can overpass (‘jump over’) 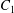 $C_{1}$ and it is then shifted back towards the flow axis as it moves away. However, the final separation
$C_{1}$ and it is then shifted back towards the flow axis as it moves away. However, the final separation 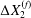 $\unicode[STIX]{x0394}X_{2}^{(f)}$ is larger than the initial one
$\unicode[STIX]{x0394}X_{2}^{(f)}$ is larger than the initial one 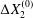 $\unicode[STIX]{x0394}X_{2}^{(0)}$. The crossing thus leads to an irreversible trajectory shift along the shear gradient (
$\unicode[STIX]{x0394}X_{2}^{(0)}$. The crossing thus leads to an irreversible trajectory shift along the shear gradient (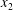 $x_{2}$-direction). This effect, which decreases with an increase of the capsule deformability and/or the initial distance
$x_{2}$-direction). This effect, which decreases with an increase of the capsule deformability and/or the initial distance 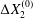 $\unicode[STIX]{x0394}X_{2}^{(0)}$, ultimately leads to self-diffusion effects in a suspension. We propose to call this crossing process the leapfrog motion. The same situation was later considered where the two spherical capsules were replaced by two red blood cells (Omori et al. Reference Omori, Ishikawa, Imai and Yamaguchi2013) or two vesicles (Gires et al. Reference Gires, Srivastav, Misbah, Podgorski and Coupier2014). In both instances, it is found that the particles do a leapfrog motion with a trajectory shift that evolves qualitatively, as found previously by Lac et al. Experimental measurements of the trajectory of liquid filled giant lipid vesicles compare well with the predictions of the flow model (Kantsler, Segre & Steinberg Reference Kantsler, Segre and Steinberg2008; Gires et al. Reference Gires, Srivastav, Misbah, Podgorski and Coupier2014). In all the aforementioned studies, the flow field around the capsules was computed by means of the boundary integral representation of the Stokes equations. As a consequence, the pair of capsules is effectively interacting in an infinite flow domain.
$\unicode[STIX]{x0394}X_{2}^{(0)}$, ultimately leads to self-diffusion effects in a suspension. We propose to call this crossing process the leapfrog motion. The same situation was later considered where the two spherical capsules were replaced by two red blood cells (Omori et al. Reference Omori, Ishikawa, Imai and Yamaguchi2013) or two vesicles (Gires et al. Reference Gires, Srivastav, Misbah, Podgorski and Coupier2014). In both instances, it is found that the particles do a leapfrog motion with a trajectory shift that evolves qualitatively, as found previously by Lac et al. Experimental measurements of the trajectory of liquid filled giant lipid vesicles compare well with the predictions of the flow model (Kantsler, Segre & Steinberg Reference Kantsler, Segre and Steinberg2008; Gires et al. Reference Gires, Srivastav, Misbah, Podgorski and Coupier2014). In all the aforementioned studies, the flow field around the capsules was computed by means of the boundary integral representation of the Stokes equations. As a consequence, the pair of capsules is effectively interacting in an infinite flow domain.
Finite differences and front tracking techniques can also be used to study the interaction problem: the advantage is that non-Newtonian or finite inertia effects in the suspending fluid can be considered. However, the computation is then usually performed in a flow domain, bounded by two walls parallel to the  $x_{1}x_{3}$-plane where the velocity is imposed (to create the simple shear flow). On the other boundaries of the box, periodic flow conditions are imposed. Doddi & Bagchi (Reference Doddi and Bagchi2008) used this technique to model the pair interaction of two initially spherical capsules, when the inertia of the flow was not negligible. They found that, when the flow Reynolds number increased, the capsules did not cross, but reversed their motion. This phenomenon was confirmed for a pair of liquid droplets (Olapade, Singh & Sarkar Reference Olapade, Singh and Sarkar2009). However, the spiralling motion reported by Doddi and Bagchi, is linked to the size of their computational domain and is a confinement effect. Indeed, for the results to be independent of the computational procedure and to be transposable to unbounded flow situations, the domain has to be large enough, typically
$x_{1}x_{3}$-plane where the velocity is imposed (to create the simple shear flow). On the other boundaries of the box, periodic flow conditions are imposed. Doddi & Bagchi (Reference Doddi and Bagchi2008) used this technique to model the pair interaction of two initially spherical capsules, when the inertia of the flow was not negligible. They found that, when the flow Reynolds number increased, the capsules did not cross, but reversed their motion. This phenomenon was confirmed for a pair of liquid droplets (Olapade, Singh & Sarkar Reference Olapade, Singh and Sarkar2009). However, the spiralling motion reported by Doddi and Bagchi, is linked to the size of their computational domain and is a confinement effect. Indeed, for the results to be independent of the computational procedure and to be transposable to unbounded flow situations, the domain has to be large enough, typically 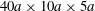 $40a\times 10a\times 5a$, for in-shear-plane crossing (Olapade et al. Reference Olapade, Singh and Sarkar2009). Pranay et al. (Reference Pranay, Anekal, Hernandez-Ortiz and Graham2010) considered the case where the suspending fluid is a dilute polymeric solution. They found that the presence of polymer leads to a decrease of the trajectory shift only when the capsule deformability is low. A recent study (Singh & Sarkar Reference Singh and Sarkar2015) considered the pair interaction of two capsules with different deformability and found that the trajectory shift is influenced by the stiffness ratio. All the studies based on finite difference and front tracking techniques only considered pairs of capsules with their centroids in the same shear plane, where they remain because of the problem symmetry.
$40a\times 10a\times 5a$, for in-shear-plane crossing (Olapade et al. Reference Olapade, Singh and Sarkar2009). Pranay et al. (Reference Pranay, Anekal, Hernandez-Ortiz and Graham2010) considered the case where the suspending fluid is a dilute polymeric solution. They found that the presence of polymer leads to a decrease of the trajectory shift only when the capsule deformability is low. A recent study (Singh & Sarkar Reference Singh and Sarkar2015) considered the pair interaction of two capsules with different deformability and found that the trajectory shift is influenced by the stiffness ratio. All the studies based on finite difference and front tracking techniques only considered pairs of capsules with their centroids in the same shear plane, where they remain because of the problem symmetry.
However, in a suspension, two nearby capsules will not necessarily have their centres of mass in the same shear plane. For example, special care has to be taken in vesicle experiments to ensure that this is approximately the case. Accordingly, Lac & Barthès-Biesel (Reference Lac and Barthès-Biesel2008) also modelled the three-dimensional motion of two capsules positioned in two different shear planes ( $\unicode[STIX]{x0394}X_{3}^{(0)}\neq 0$). In this case, a sideways leapfrog motion occurs with a maximum trajectory displacement along both the
$\unicode[STIX]{x0394}X_{3}^{(0)}\neq 0$). In this case, a sideways leapfrog motion occurs with a maximum trajectory displacement along both the 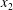 $x_{2}$- and
$x_{2}$- and 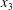 $x_{3}$-directions, which decreases as
$x_{3}$-directions, which decreases as 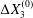 $\unicode[STIX]{x0394}X_{3}^{(0)}$ and/or capsule deformability increase. Lac and Barthès-Biesel also showed that the final trajectory shift along the
$\unicode[STIX]{x0394}X_{3}^{(0)}$ and/or capsule deformability increase. Lac and Barthès-Biesel also showed that the final trajectory shift along the 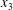 $x_{3}$-axis is indeed smaller than the one along the velocity gradient
$x_{3}$-axis is indeed smaller than the one along the velocity gradient 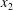 $x_{2}$-axis (approximately one third), but present nevertheless. This was also globally confirmed by Gires et al. (Reference Gires, Srivastav, Misbah, Podgorski and Coupier2014) for vesicles.
$x_{2}$-axis (approximately one third), but present nevertheless. This was also globally confirmed by Gires et al. (Reference Gires, Srivastav, Misbah, Podgorski and Coupier2014) for vesicles.
However, in all aforementioned studies, the two capsules always had a significant initial relative velocity, obtained by means of 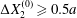 $\unicode[STIX]{x0394}X_{2}^{(0)}\geqslant 0.5a$. This choice was made to avoid very long computations. The only exceptions are due to Lac et al. (Reference Lac, Morel and Barthès-Biesel2007) and Omori et al. (Reference Omori, Ishikawa, Imai and Yamaguchi2013), who showed that, for two capsules located on the same streamline (
$\unicode[STIX]{x0394}X_{2}^{(0)}\geqslant 0.5a$. This choice was made to avoid very long computations. The only exceptions are due to Lac et al. (Reference Lac, Morel and Barthès-Biesel2007) and Omori et al. (Reference Omori, Ishikawa, Imai and Yamaguchi2013), who showed that, for two capsules located on the same streamline ( $\unicode[STIX]{x0394}X_{1}^{(0)}\neq 0,\unicode[STIX]{x0394}X_{2}^{(0)}=\unicode[STIX]{x0394}X_{3}^{(0)}=0$), the perturbation created by the deformation and membrane rotation of the two capsules created a small but finite velocity field that displaced the centroids along the
$\unicode[STIX]{x0394}X_{1}^{(0)}\neq 0,\unicode[STIX]{x0394}X_{2}^{(0)}=\unicode[STIX]{x0394}X_{3}^{(0)}=0$), the perturbation created by the deformation and membrane rotation of the two capsules created a small but finite velocity field that displaced the centroids along the 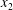 $x_{2}$-axis and led to a relative velocity of the capsules and to a leapfrog motion. The result was interesting as it showed that such initial conditions led to the largest self-diffusion effect. The conclusion of this review is that there is presently no information on the interaction of two capsules when their centres are located in the
$x_{2}$-axis and led to a relative velocity of the capsules and to a leapfrog motion. The result was interesting as it showed that such initial conditions led to the largest self-diffusion effect. The conclusion of this review is that there is presently no information on the interaction of two capsules when their centres are located in the 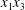 $x_{1}x_{3}$-plane.
$x_{1}x_{3}$-plane.
The objective of this paper is to fill this gap and to investigate the three-dimensional motion of two capsules when their centroids are in or near the same 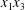 $x_{1}x_{3}$-plane. We will take advantage of the computational technique that we have developed, based on the coupling of a boundary integral to compute the flow and finite elements to compute the capsule wall mechanics (Walter et al. Reference Walter, Salsac, Barthès-Biesel and le Tallec2010). This coupling has proved to be very stable in a number of situations where long transient motion of a single capsule needed to be monitored (Walter, Salsac & Barthès-Biesel Reference Walter, Salsac and Barthès-Biesel2011; Hu, Salsac & Barthès-Biesel Reference Hu, Salsac and Barthès-Biesel2012; Dupont, Salsac & Barthès-Biesel Reference Dupont, Salsac and Barthès-Biesel2013; Dupont et al. Reference Dupont, Delahaye, Barthès-Biesel and Salsac2016). We will see that a new interaction mode is revealed: given the choice, the capsules oscillate around the shear gradient axis, rather than around the vorticity axis. We call this interaction mode the minuet motion, as it is similar to the one reported for Volvox algae (Drescher et al. Reference Drescher, Leptos, Tuval, Ishikawa, Pedley and Goldstein2009), albeit for different hydrodynamic interactions.
$x_{1}x_{3}$-plane. We will take advantage of the computational technique that we have developed, based on the coupling of a boundary integral to compute the flow and finite elements to compute the capsule wall mechanics (Walter et al. Reference Walter, Salsac, Barthès-Biesel and le Tallec2010). This coupling has proved to be very stable in a number of situations where long transient motion of a single capsule needed to be monitored (Walter, Salsac & Barthès-Biesel Reference Walter, Salsac and Barthès-Biesel2011; Hu, Salsac & Barthès-Biesel Reference Hu, Salsac and Barthès-Biesel2012; Dupont, Salsac & Barthès-Biesel Reference Dupont, Salsac and Barthès-Biesel2013; Dupont et al. Reference Dupont, Delahaye, Barthès-Biesel and Salsac2016). We will see that a new interaction mode is revealed: given the choice, the capsules oscillate around the shear gradient axis, rather than around the vorticity axis. We call this interaction mode the minuet motion, as it is similar to the one reported for Volvox algae (Drescher et al. Reference Drescher, Leptos, Tuval, Ishikawa, Pedley and Goldstein2009), albeit for different hydrodynamic interactions.
The paper is organized as follows: the problem is set out in § 2 together with a short description of the numerical method. The different types of capsule interaction are presented in § 3, where we also discuss the main factors that determine the motion type. In § 4, we analyse which factors determine the motion type and illustrate the area of space where oscillatory motion is expected to occur. In § 5, we then study the consequences on the trajectory shift and self-diffusion phenomena in the suspension. In the final § 6, we summarize the findings and provide a conclusion.
2 Problem statement and numerical method
2.1 Problem description

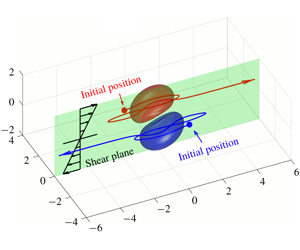
Figure 1. Two capsules flowing in simple shear flow. The reference frame is linked to capsule  $C_{1}$ and the coordinate system is centred on it. The centre of
$C_{1}$ and the coordinate system is centred on it. The centre of 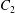 $C_{2}$ is initially positioned at
$C_{2}$ is initially positioned at 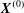 $\boldsymbol{X}^{(0)}$.
$\boldsymbol{X}^{(0)}$.
Two identical spherical capsules 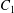 $C_{1}$ and
$C_{1}$ and 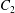 $C_{2}$ (radius
$C_{2}$ (radius  $a$), filled with a Newtonian liquid (viscosity
$a$), filled with a Newtonian liquid (viscosity 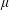 $\unicode[STIX]{x1D707}$, density
$\unicode[STIX]{x1D707}$, density  $\unicode[STIX]{x1D70C}$) and enclosed by a very thin hyper-elastic membrane (surface shear modulus
$\unicode[STIX]{x1D70C}$) and enclosed by a very thin hyper-elastic membrane (surface shear modulus  $G_{s}$ and area dilation modulus
$G_{s}$ and area dilation modulus 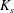 $K_{s}$), are freely suspended in another Newtonian liquid (viscosity
$K_{s}$), are freely suspended in another Newtonian liquid (viscosity  $\unicode[STIX]{x1D707}$, density
$\unicode[STIX]{x1D707}$, density  $\unicode[STIX]{x1D70C}$) and subjected to a simple shear flow with shear rate
$\unicode[STIX]{x1D70C}$) and subjected to a simple shear flow with shear rate 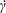 $\dot{\unicode[STIX]{x1D6FE}}$. Inertia effect is neglected. The capsules centroids are denoted
$\dot{\unicode[STIX]{x1D6FE}}$. Inertia effect is neglected. The capsules centroids are denoted 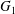 $G_{1}$ and
$G_{1}$ and 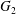 $G_{2}$. We use a reference frame centred on
$G_{2}$. We use a reference frame centred on 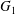 $G_{1}$, that moves with it (figure 1). Our objective is to study the interaction process between the two capsules as they are convected by the flow and, specifically, to compute the evolution of the velocity
$G_{1}$, that moves with it (figure 1). Our objective is to study the interaction process between the two capsules as they are convected by the flow and, specifically, to compute the evolution of the velocity 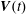 $\boldsymbol{V}(t)$ and position
$\boldsymbol{V}(t)$ and position 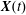 $\boldsymbol{X}(t)$ of
$\boldsymbol{X}(t)$ of 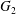 $G_{2}$ with time
$G_{2}$ with time  $t$.
$t$.
The undisturbed flow 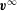 $\boldsymbol{v}^{\infty }$ of the external liquid is given by
$\boldsymbol{v}^{\infty }$ of the external liquid is given by
 $$\begin{eqnarray}v_{1}^{\infty }(\boldsymbol{x})=\dot{\unicode[STIX]{x1D6FE}}x_{2};\quad v_{2}^{\infty }(\boldsymbol{x})=v_{3}^{\infty }(\boldsymbol{x})=0.\end{eqnarray}$$
$$\begin{eqnarray}v_{1}^{\infty }(\boldsymbol{x})=\dot{\unicode[STIX]{x1D6FE}}x_{2};\quad v_{2}^{\infty }(\boldsymbol{x})=v_{3}^{\infty }(\boldsymbol{x})=0.\end{eqnarray}$$Note that, since the problem is inertialess, the flow field has the same expression (2.1) in a laboratory reference frame. The motion of the internal and external fluids is governed by the Stokes equations, with associated boundary conditions given by:
(i) vanishing flow perturbation far from the capsules:
(2.2) $$\begin{eqnarray}\boldsymbol{v}^{ext}(\boldsymbol{x})\rightarrow \boldsymbol{v}^{\infty }(\boldsymbol{x})\quad \text{as }\Vert \boldsymbol{x}-\boldsymbol{x}(G_{\unicode[STIX]{x1D6FC}})\Vert \rightarrow \infty \quad \unicode[STIX]{x1D6FC}=1,2;\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}^{ext}(\boldsymbol{x})\rightarrow \boldsymbol{v}^{\infty }(\boldsymbol{x})\quad \text{as }\Vert \boldsymbol{x}-\boldsymbol{x}(G_{\unicode[STIX]{x1D6FC}})\Vert \rightarrow \infty \quad \unicode[STIX]{x1D6FC}=1,2;\end{eqnarray}$$(ii) at a material point
 $\boldsymbol{x}$ located on the membrane of either capsule (2.3)
$\boldsymbol{x}$ located on the membrane of either capsule (2.3) $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{v}^{ext}(\boldsymbol{x})=\boldsymbol{v}^{int}(\boldsymbol{x})=\dot{\boldsymbol{x}}, & \displaystyle\end{eqnarray}$$(2.4)
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{v}^{ext}(\boldsymbol{x})=\boldsymbol{v}^{int}(\boldsymbol{x})=\dot{\boldsymbol{x}}, & \displaystyle\end{eqnarray}$$(2.4) $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{q}+\unicode[STIX]{x1D6FB}_{s}\boldsymbol{\cdot }\boldsymbol{T}=\mathbf{0}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{q}+\unicode[STIX]{x1D6FB}_{s}\boldsymbol{\cdot }\boldsymbol{T}=\mathbf{0}, & \displaystyle\end{eqnarray}$$
where the superscript 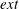 $ext$ or
$ext$ or 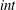 $int$ refers respectively to the suspending fluid or to the capsule internal liquid. The jump of viscous traction across the membranes is
$int$ refers respectively to the suspending fluid or to the capsule internal liquid. The jump of viscous traction across the membranes is 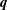 $\boldsymbol{q}$, the in-plane elastic tension tensor in the membrane is denoted
$\boldsymbol{q}$, the in-plane elastic tension tensor in the membrane is denoted 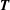 $\boldsymbol{T}$ and
$\boldsymbol{T}$ and 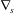 $\unicode[STIX]{x1D6FB}_{s}$ is the surface gradient operator. Equation (2.4) is the membrane equilibrium equation, which expresses the dynamic coupling between the solid membranes and the fluids.
$\unicode[STIX]{x1D6FB}_{s}$ is the surface gradient operator. Equation (2.4) is the membrane equilibrium equation, which expresses the dynamic coupling between the solid membranes and the fluids.
As this fluid–structure interaction problem is now classical, we will only present the main hypotheses used here and refer the reader to the comprehensive review of Barthès-Biesel (Reference Barthès-Biesel2016). The fluid velocity at any point  $\boldsymbol{x}$ is written as a boundary integral on the surfaces
$\boldsymbol{x}$ is written as a boundary integral on the surfaces 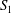 $S_{1}$ and
$S_{1}$ and 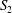 $S_{2}$ of the two capsules (Lac et al. Reference Lac, Morel and Barthès-Biesel2007)
$S_{2}$ of the two capsules (Lac et al. Reference Lac, Morel and Barthès-Biesel2007)
 $$\begin{eqnarray}\boldsymbol{v}(\boldsymbol{x})=\boldsymbol{v}^{\infty }(\boldsymbol{x})-\frac{1}{8\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}}\int _{S_{1}\cup S_{2}}\boldsymbol{J}(\boldsymbol{x},\boldsymbol{y})\boldsymbol{\cdot }\boldsymbol{q}(\boldsymbol{y})\,\text{d}S(\boldsymbol{y}),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}(\boldsymbol{x})=\boldsymbol{v}^{\infty }(\boldsymbol{x})-\frac{1}{8\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}}\int _{S_{1}\cup S_{2}}\boldsymbol{J}(\boldsymbol{x},\boldsymbol{y})\boldsymbol{\cdot }\boldsymbol{q}(\boldsymbol{y})\,\text{d}S(\boldsymbol{y}),\end{eqnarray}$$ where 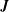 $\boldsymbol{J}$ is the free space Green’s function given by
$\boldsymbol{J}$ is the free space Green’s function given by
 $$\begin{eqnarray}\boldsymbol{J}(\boldsymbol{x},\boldsymbol{y})=\frac{\unicode[STIX]{x1D644}}{\Vert \boldsymbol{x}-\boldsymbol{y}\Vert }+\frac{(\boldsymbol{x}-\boldsymbol{y})\otimes (\boldsymbol{x}-\boldsymbol{y})}{\Vert \boldsymbol{x}-\boldsymbol{y}\Vert ^{3}},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{J}(\boldsymbol{x},\boldsymbol{y})=\frac{\unicode[STIX]{x1D644}}{\Vert \boldsymbol{x}-\boldsymbol{y}\Vert }+\frac{(\boldsymbol{x}-\boldsymbol{y})\otimes (\boldsymbol{x}-\boldsymbol{y})}{\Vert \boldsymbol{x}-\boldsymbol{y}\Vert ^{3}},\end{eqnarray}$$ where  $\unicode[STIX]{x1D644}$ is the identity tensor. The pressure
$\unicode[STIX]{x1D644}$ is the identity tensor. The pressure 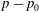 $p-p_{0}$ at a point
$p-p_{0}$ at a point  $\boldsymbol{x}$ is given by
$\boldsymbol{x}$ is given by
 $$\begin{eqnarray}p(\boldsymbol{x})-p_{0}=-\frac{1}{4\unicode[STIX]{x03C0}}\int _{S_{1}\cup S_{2}}\frac{\boldsymbol{q}(\boldsymbol{y})\boldsymbol{\cdot }(\boldsymbol{x}-\boldsymbol{y})}{\Vert \boldsymbol{x}-\boldsymbol{y}\Vert ^{3}}\,\text{d}S(\boldsymbol{y}),\end{eqnarray}$$
$$\begin{eqnarray}p(\boldsymbol{x})-p_{0}=-\frac{1}{4\unicode[STIX]{x03C0}}\int _{S_{1}\cup S_{2}}\frac{\boldsymbol{q}(\boldsymbol{y})\boldsymbol{\cdot }(\boldsymbol{x}-\boldsymbol{y})}{\Vert \boldsymbol{x}-\boldsymbol{y}\Vert ^{3}}\,\text{d}S(\boldsymbol{y}),\end{eqnarray}$$ where  $p_{0}$ denotes the far field pressure.
$p_{0}$ denotes the far field pressure.
The capsule membrane is assumed to be an infinitely thin sheet of a three-dimensional isotropic volume incompressible material that satisfies a neo-Hookean (NH) constitutive law. Bending resistance is neglected. The membrane constitutive law relates the principal elastic tensions (forces per unit arclength measured in the membrane plane) 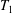 $T_{1}$ and
$T_{1}$ and 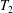 $T_{2}$ to the two principal extension ratios
$T_{2}$ to the two principal extension ratios 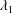 $\unicode[STIX]{x1D706}_{1}$ and
$\unicode[STIX]{x1D706}_{1}$ and 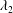 $\unicode[STIX]{x1D706}_{2}$
$\unicode[STIX]{x1D706}_{2}$
 $$\begin{eqnarray}T_{1}=\frac{G_{s}}{\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D706}_{2}}\left[\unicode[STIX]{x1D706}_{1}^{2}-\frac{1}{(\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D706}_{2})^{2}}\right],\end{eqnarray}$$
$$\begin{eqnarray}T_{1}=\frac{G_{s}}{\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D706}_{2}}\left[\unicode[STIX]{x1D706}_{1}^{2}-\frac{1}{(\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D706}_{2})^{2}}\right],\end{eqnarray}$$ with a similar expression for 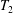 $T_{2}$, where the subscripts 1 and 2 are permuted. For simplicity, we have denoted these principal directions 1 and 2, but they should not be confused with the Cartesian directions in space. The surface shear elastic modulus
$T_{2}$, where the subscripts 1 and 2 are permuted. For simplicity, we have denoted these principal directions 1 and 2, but they should not be confused with the Cartesian directions in space. The surface shear elastic modulus 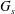 $G_{s}$ and area dilation modulus
$G_{s}$ and area dilation modulus 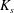 $K_{s}$ are related by
$K_{s}$ are related by  $K_{s}=3G_{s}$ (Barthès-Biesel Reference Barthès-Biesel2016). The corresponding total deformation energy of the membrane of one capsule is given by
$K_{s}=3G_{s}$ (Barthès-Biesel Reference Barthès-Biesel2016). The corresponding total deformation energy of the membrane of one capsule is given by
 $$\begin{eqnarray}W=\frac{G_{s}}{2}\int _{S}\left(\unicode[STIX]{x1D706}_{1}^{2}+\unicode[STIX]{x1D706}_{3}^{2}-3+\frac{1}{\unicode[STIX]{x1D706}_{1}^{2}\unicode[STIX]{x1D706}_{2}^{2}}\right)\,\text{d}S,\end{eqnarray}$$
$$\begin{eqnarray}W=\frac{G_{s}}{2}\int _{S}\left(\unicode[STIX]{x1D706}_{1}^{2}+\unicode[STIX]{x1D706}_{3}^{2}-3+\frac{1}{\unicode[STIX]{x1D706}_{1}^{2}\unicode[STIX]{x1D706}_{2}^{2}}\right)\,\text{d}S,\end{eqnarray}$$ where 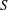 $S$ stands for either
$S$ stands for either 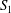 $S_{1}$ or
$S_{1}$ or 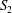 $S_{2}$.
$S_{2}$.
The main parameters are the capillary number
 $$\begin{eqnarray}Ca=\frac{\unicode[STIX]{x1D707}\dot{\unicode[STIX]{x1D6FE}}a}{G_{s}},\end{eqnarray}$$
$$\begin{eqnarray}Ca=\frac{\unicode[STIX]{x1D707}\dot{\unicode[STIX]{x1D6FE}}a}{G_{s}},\end{eqnarray}$$ which measures the relative stiffness of the capsule, and the initial position of  $G_{2}$ at time
$G_{2}$ at time 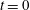 $t=0$, when the flow is suddenly started
$t=0$, when the flow is suddenly started
 $$\begin{eqnarray}\boldsymbol{X}(0)=\boldsymbol{X}^{(0)}=\{X_{1}^{(0)},X_{2}^{(0)},X_{3}^{(0)}\}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{X}(0)=\boldsymbol{X}^{(0)}=\{X_{1}^{(0)},X_{2}^{(0)},X_{3}^{(0)}\}.\end{eqnarray}$$ We shall discuss the typical case where 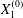 $X_{1}^{(0)}$ and
$X_{1}^{(0)}$ and 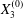 $X_{3}^{(0)}$ are negative while
$X_{3}^{(0)}$ are negative while  $X_{2}^{(0)}$ is positive: the flow of
$X_{2}^{(0)}$ is positive: the flow of 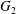 $G_{2}$ occurs from left to right in the trajectory figures. The case
$G_{2}$ occurs from left to right in the trajectory figures. The case 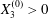 $X_{3}^{(0)}>0$ provides the same results as the typical case since it corresponds to the symmetric configuration with respect to the shear plane. Positive values of
$X_{3}^{(0)}>0$ provides the same results as the typical case since it corresponds to the symmetric configuration with respect to the shear plane. Positive values of 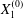 $X_{1}^{(0)}$ and negative ones for
$X_{1}^{(0)}$ and negative ones for 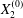 $X_{2}^{(0)}$ correspond to the mirror image of the typical case, with respect to the
$X_{2}^{(0)}$ correspond to the mirror image of the typical case, with respect to the 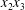 $x_{2}x_{3}$-plane. When the crossing process is completed, the final steady position of
$x_{2}x_{3}$-plane. When the crossing process is completed, the final steady position of 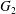 $G_{2}$ is
$G_{2}$ is  $\{X_{1}^{(f)},X_{2}^{(f)},X_{3}^{(f)}\}$. We define the final trajectory shifts of the capsule
$\{X_{1}^{(f)},X_{2}^{(f)},X_{3}^{(f)}\}$. We define the final trajectory shifts of the capsule
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{2}=|X_{2}^{(f)}|-|X_{2}^{(0)}|,\quad \unicode[STIX]{x1D6FF}_{3}=|X_{3}^{(f)}|-|X_{3}^{(0)}|,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{2}=|X_{2}^{(f)}|-|X_{2}^{(0)}|,\quad \unicode[STIX]{x1D6FF}_{3}=|X_{3}^{(f)}|-|X_{3}^{(0)}|,\end{eqnarray}$$ which are computed for 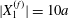 $|X_{1}^{(f)}|=10a$.
$|X_{1}^{(f)}|=10a$.
2.2 Numerical method
The fluid–structure interaction problem is solved by means of the numerical scheme that couples a boundary integral method (BI) to solve the fluid flow and the finite element method (FE) to solve the membrane mechanics (Walter et al. Reference Walter, Salsac, Barthès-Biesel and le Tallec2010; Hu et al. Reference Hu, Salsac and Barthès-Biesel2012). This method is well adapted to Stokes flows and has the advantage of requiring the discretization of the capsule surfaces  $S_{1}$ and
$S_{1}$ and  $S_{2}$ only. It automatically accounts for an unbounded fluid domain. The model inputs are the capillary number
$S_{2}$ only. It automatically accounts for an unbounded fluid domain. The model inputs are the capillary number  $Ca$ and the initial position
$Ca$ and the initial position 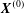 $\boldsymbol{X}^{(0)}$ of capsule
$\boldsymbol{X}^{(0)}$ of capsule 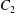 $C_{2}$. Following Lac et al. (Reference Lac, Morel and Barthès-Biesel2007), we use the fact that the two capsules are identical to centre the flow field on the midpoint
$C_{2}$. Following Lac et al. (Reference Lac, Morel and Barthès-Biesel2007), we use the fact that the two capsules are identical to centre the flow field on the midpoint 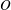 $O$ of
$O$ of 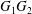 $G_{1}G_{2}$, so that (2.5) can be solved on only one capsule and becomes
$G_{1}G_{2}$, so that (2.5) can be solved on only one capsule and becomes
 $$\begin{eqnarray}\boldsymbol{v}(\boldsymbol{x})=\boldsymbol{v}^{\infty }(\boldsymbol{x})-\frac{1}{8\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}}\int _{S_{2}}[\boldsymbol{J}(\boldsymbol{x},\boldsymbol{y})-\boldsymbol{J}(\boldsymbol{x},-\boldsymbol{y})]\boldsymbol{\cdot }\boldsymbol{q}(\boldsymbol{y})\,\text{d}S(\boldsymbol{y}).\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}(\boldsymbol{x})=\boldsymbol{v}^{\infty }(\boldsymbol{x})-\frac{1}{8\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}}\int _{S_{2}}[\boldsymbol{J}(\boldsymbol{x},\boldsymbol{y})-\boldsymbol{J}(\boldsymbol{x},-\boldsymbol{y})]\boldsymbol{\cdot }\boldsymbol{q}(\boldsymbol{y})\,\text{d}S(\boldsymbol{y}).\end{eqnarray}$$ The capsule surface 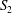 $S_{2}$ is discretized using
$S_{2}$ is discretized using 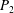 $P_{2}$ triangle elements, in which 6 nodes are allocated at the vertices and the middle of each side. The mesh is generated from the initial spherical shape by projecting a regular icosahedron to the sphere and then subdividing each element subsequently to the desired precision. A mesh of 1280 elements and 2562 nodes has been used in all the simulations, corresponding to a characteristic mesh size
$P_{2}$ triangle elements, in which 6 nodes are allocated at the vertices and the middle of each side. The mesh is generated from the initial spherical shape by projecting a regular icosahedron to the sphere and then subdividing each element subsequently to the desired precision. A mesh of 1280 elements and 2562 nodes has been used in all the simulations, corresponding to a characteristic mesh size 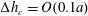 $\unicode[STIX]{x0394}h_{c}=O(0.1a)$. Such a spatial discretization has been shown to lead to a relative error of order
$\unicode[STIX]{x0394}h_{c}=O(0.1a)$. Such a spatial discretization has been shown to lead to a relative error of order 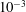 $10^{-3}$ on the Taylor deformation of a single capsule in shear flow (Walter et al. Reference Walter, Salsac, Barthès-Biesel and le Tallec2010). Furthermore, it can withstand some membrane compression without creating any numerical instability (Hu et al. Reference Hu, Salsac and Barthès-Biesel2012). The explicit time iteration is stable only if the time step is such that
$10^{-3}$ on the Taylor deformation of a single capsule in shear flow (Walter et al. Reference Walter, Salsac, Barthès-Biesel and le Tallec2010). Furthermore, it can withstand some membrane compression without creating any numerical instability (Hu et al. Reference Hu, Salsac and Barthès-Biesel2012). The explicit time iteration is stable only if the time step is such that 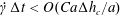 $\dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x0394}t<O(Ca\unicode[STIX]{x0394}h_{c}/a)$ (Walter et al. Reference Walter, Salsac, Barthès-Biesel and le Tallec2010). In the case of a NH membrane and
$\dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x0394}t<O(Ca\unicode[STIX]{x0394}h_{c}/a)$ (Walter et al. Reference Walter, Salsac, Barthès-Biesel and le Tallec2010). In the case of a NH membrane and 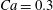 $Ca=0.3$,
$Ca=0.3$, 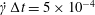 $\dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x0394}t=5\times 10^{-4}$ allows us to compute the capsule trajectory over long times without stability issues. We stop the computation when the distance
$\dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x0394}t=5\times 10^{-4}$ allows us to compute the capsule trajectory over long times without stability issues. We stop the computation when the distance 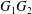 $G_{1}G_{2}$ is larger than
$G_{1}G_{2}$ is larger than 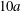 $10a$.
$10a$.
At time 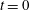 $t=0$,
$t=0$, 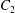 $C_{2}$ (positioned at
$C_{2}$ (positioned at 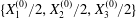 $\{X_{1}^{(0)}/2,X_{2}^{(0)}/2,X_{3}^{(0)}/2\}$) and
$\{X_{1}^{(0)}/2,X_{2}^{(0)}/2,X_{3}^{(0)}/2\}$) and  $C_{1}$ (positioned at
$C_{1}$ (positioned at 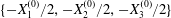 $\{-X_{1}^{(0)}/2,-X_{2}^{(0)}/2,-X_{3}^{(0)}/2\}$) are subjected to the sudden start of the flow. The model follows the motion of the capsule membrane over time. At any time, the model can thus output the position of the surface nodes, from which it is possible to infer, for each capsule, the deformation and elastic tensions in the membrane as well as the position and velocity of the centroid. The knowledge of this velocity allows us to transcript the results in the reference frame linked to
$\{-X_{1}^{(0)}/2,-X_{2}^{(0)}/2,-X_{3}^{(0)}/2\}$) are subjected to the sudden start of the flow. The model follows the motion of the capsule membrane over time. At any time, the model can thus output the position of the surface nodes, from which it is possible to infer, for each capsule, the deformation and elastic tensions in the membrane as well as the position and velocity of the centroid. The knowledge of this velocity allows us to transcript the results in the reference frame linked to  $C_{1}$.
$C_{1}$.
The accuracy of the numerical model is checked by comparing capsules trajectories with those obtained by Lac et al. (Reference Lac, Morel and Barthès-Biesel2007) and Lac & Barthès-Biesel (Reference Lac and Barthès-Biesel2008), and also by assessing the influence of the time step and of the spatial discretization of the capsule membranes (see the Appendix): the conclusion is that the centroid trajectories are accurate to within  $0.05a$.
$0.05a$.
3 Types of capsule interaction: simple crossing (leapfrog) or minuet motion
A major finding of our work is that, depending on the initial position of 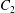 $C_{2}$, there are two types of motion:
$C_{2}$, there are two types of motion:
(i) Simple crossing (also denoted leapfrog):
 $C_{2}$ catches up with
$C_{2}$ catches up with  $C_{1}$, interacts and goes away. The two capsules are not necessarily in the same shear plane.
$C_{1}$, interacts and goes away. The two capsules are not necessarily in the same shear plane.(ii) Minuet motion:
 $C_{2}$ catches up with
$C_{2}$ catches up with  $C_{1}$, interacts, overpasses
$C_{1}$, interacts, overpasses  $C_{1}$, reverses its motion and repeats the process one, two or three times before getting away.
$C_{1}$, reverses its motion and repeats the process one, two or three times before getting away.
The two motions are illustrated and analysed in the following.
3.1 Single interaction: leapfrog motion
As a reference, we consider the situation where the two capsules are in the shear plane on the same streamline (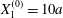 $X_{1}^{(0)}=10a$,
$X_{1}^{(0)}=10a$, 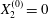 $X_{2}^{(0)}=0$,
$X_{2}^{(0)}=0$, 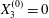 $X_{3}^{(0)}=0$,
$X_{3}^{(0)}=0$,  $Ca=0.3$). Similar computations have been made by Lac et al. (Reference Lac, Morel and Barthès-Biesel2007) for pre-inflated capsules, but only the value of the final trajectory shift is reported. Under Stokes flow conditions, the capsules must remain in this plane. The trajectory of
$Ca=0.3$). Similar computations have been made by Lac et al. (Reference Lac, Morel and Barthès-Biesel2007) for pre-inflated capsules, but only the value of the final trajectory shift is reported. Under Stokes flow conditions, the capsules must remain in this plane. The trajectory of 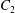 $C_{2}$ is shown in figure 2(a,b) (movie 1 available at https://doi.org/10.1017/jfm.2020.181).
$C_{2}$ is shown in figure 2(a,b) (movie 1 available at https://doi.org/10.1017/jfm.2020.181).

Figure 2. Leapfrog motion of two capsules with their centres in the same shear plane (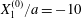 $X_{1}^{(0)}/a=-10$,
$X_{1}^{(0)}/a=-10$, 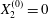 $X_{2}^{(0)}=0$,
$X_{2}^{(0)}=0$, 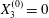 $X_{3}^{(0)}=0$,
$X_{3}^{(0)}=0$, 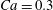 $Ca=0.3$). (a) Three-dimensional view of the trajectory of
$Ca=0.3$). (a) Three-dimensional view of the trajectory of 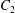 $C_{2}$. (b)
$C_{2}$. (b) 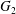 $G_{2}$ trajectory in the shear plane. (c) Three-dimensional view of the deformed capsules at
$G_{2}$ trajectory in the shear plane. (c) Three-dimensional view of the deformed capsules at 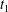 $t_{1}$ when
$t_{1}$ when 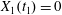 $X_{1}(t_{1})=0$. (d–f)
$X_{1}(t_{1})=0$. (d–f) 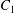 $C_{1}$ intersections with the three coordinates planes at
$C_{1}$ intersections with the three coordinates planes at 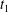 $t_{1}$.
$t_{1}$.

Figure 3. Evolution of 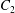 $C_{2}$ velocity during a leapfrog (
$C_{2}$ velocity during a leapfrog ( $X_{1}^{(0)}/a=-10$,
$X_{1}^{(0)}/a=-10$, 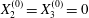 $X_{2}^{(0)}=X_{3}^{(0)}=0$) or minuet (
$X_{2}^{(0)}=X_{3}^{(0)}=0$) or minuet (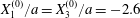 $X_{1}^{(0)}/a=X_{3}^{(0)}/a=-2.6$,
$X_{1}^{(0)}/a=X_{3}^{(0)}/a=-2.6$, 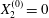 $X_{2}^{(0)}=0$) for
$X_{2}^{(0)}=0$) for 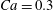 $Ca=0.3$.
$Ca=0.3$.

Figure 4. Pressure and membrane energy evolution during the leapfrog and minuet motions for 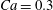 $Ca=0.3$. (a) Pressure
$Ca=0.3$. (a) Pressure 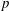 $p$ at the mid-point between
$p$ at the mid-point between 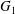 $G_{1}$ and
$G_{1}$ and 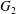 $G_{2}$; (b) membrane elastic energy
$G_{2}$; (b) membrane elastic energy 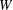 $W$. Leapfrog:
$W$. Leapfrog: 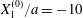 $X_{1}^{(0)}/a=-10$,
$X_{1}^{(0)}/a=-10$, 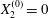 $X_{2}^{(0)}=0$,
$X_{2}^{(0)}=0$, 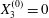 $X_{3}^{(0)}=0$. Minuet:
$X_{3}^{(0)}=0$. Minuet:  $X_{1}^{(0)}/a=-2.6$,
$X_{1}^{(0)}/a=-2.6$, 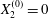 $X_{2}^{(0)}=0$,
$X_{2}^{(0)}=0$,  $X_{3}^{(0)}/a=-2.6$.
$X_{3}^{(0)}/a=-2.6$.
When the flow is started, the two capsules are far enough from each other that they behave as if they were almost alone in the fluid. Within 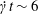 $\dot{\unicode[STIX]{x1D6FE}}t\sim 6$ they reach a roughly ellipsoidal shape around which the membrane rotates, as shown in figure 2(d) (see the review by Barthès-Biesel (Reference Barthès-Biesel2016)). The deformation and rotation of
$\dot{\unicode[STIX]{x1D6FE}}t\sim 6$ they reach a roughly ellipsoidal shape around which the membrane rotates, as shown in figure 2(d) (see the review by Barthès-Biesel (Reference Barthès-Biesel2016)). The deformation and rotation of  $C_{1}$ lead to a stresslet that creates a small velocity field and a small depression. This perturbation displaces
$C_{1}$ lead to a stresslet that creates a small velocity field and a small depression. This perturbation displaces  $C_{2}$ along the velocity gradient in the direction that moves it towards
$C_{2}$ along the velocity gradient in the direction that moves it towards 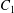 $C_{1}$, as shown in figure 2(b). Note that this phenomenon is the opposite of the one observed by Doddi & Bagchi (Reference Doddi and Bagchi2008) when inertia is taken into account. As a consequence,
$C_{1}$, as shown in figure 2(b). Note that this phenomenon is the opposite of the one observed by Doddi & Bagchi (Reference Doddi and Bagchi2008) when inertia is taken into account. As a consequence,  $V_{2}(t)>0$ for
$V_{2}(t)>0$ for  $t>0$ and
$t>0$ and 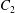 $C_{2}$ is convected towards
$C_{2}$ is convected towards  $C_{1}$, as shown in figure 2(a,b). The only way for
$C_{1}$, as shown in figure 2(a,b). The only way for 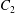 $C_{2}$ to pass
$C_{2}$ to pass  $C_{1}$ is to ‘jump’ over it in the
$C_{1}$ is to ‘jump’ over it in the  $x_{1}x_{2}$-plane (thus the term ‘leapfrog motion’). The fact that the motion is constrained to the shear plane leads to a high velocity difference
$x_{1}x_{2}$-plane (thus the term ‘leapfrog motion’). The fact that the motion is constrained to the shear plane leads to a high velocity difference  $\Vert \boldsymbol{V}-\boldsymbol{v}^{\infty }\Vert /\dot{\unicode[STIX]{x1D6FE}}a$ in the
$\Vert \boldsymbol{V}-\boldsymbol{v}^{\infty }\Vert /\dot{\unicode[STIX]{x1D6FE}}a$ in the 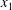 $x_{1}$- and
$x_{1}$- and 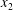 $x_{2}$-directions (figure 3). The evolution of the pressure at the midpoint between
$x_{2}$-directions (figure 3). The evolution of the pressure at the midpoint between 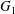 $G_{1}$ and
$G_{1}$ and 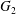 $G_{2}$ (2.7) can also explain the interaction phenomenon: indeed, as
$G_{2}$ (2.7) can also explain the interaction phenomenon: indeed, as 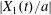 $|X_{1}(t)/a|$ decreases, the pressure in the lubrication film between the two capsules increases (figure 4a) and pushes
$|X_{1}(t)/a|$ decreases, the pressure in the lubrication film between the two capsules increases (figure 4a) and pushes 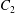 $C_{2}$ in the
$C_{2}$ in the  $x_{2}$-direction, along which the maximum displacement of
$x_{2}$-direction, along which the maximum displacement of 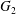 $G_{2}$ is
$G_{2}$ is 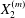 $X_{2}^{(m)}$. As
$X_{2}^{(m)}$. As  $C_{2}$ overtakes
$C_{2}$ overtakes 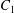 $C_{1}$, the widening of the lubrication film leads to a depression (figure 4a), which decreases
$C_{1}$, the widening of the lubrication film leads to a depression (figure 4a), which decreases 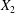 $X_{2}$, until a final steady value
$X_{2}$, until a final steady value 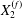 $X_{2}^{(f)}$ is reached when the two capsules are far apart (
$X_{2}^{(f)}$ is reached when the two capsules are far apart (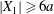 $|X_{1}|\geqslant 6a$, in this case). The final trajectory shift
$|X_{1}|\geqslant 6a$, in this case). The final trajectory shift 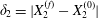 $\unicode[STIX]{x1D6FF}_{2}=|X_{2}^{(f)}-X_{2}^{(0)}|$ is
$\unicode[STIX]{x1D6FF}_{2}=|X_{2}^{(f)}-X_{2}^{(0)}|$ is  $0.9a$, and is equal to the one found by Lac et al. under the same flow situation for a 5 % pre-inflation. The finite value of
$0.9a$, and is equal to the one found by Lac et al. under the same flow situation for a 5 % pre-inflation. The finite value of 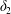 $\unicode[STIX]{x1D6FF}_{2}$ indicates that the two capsule interaction leads to self-diffusion effects in a dilute suspension of capsules. The deformed profiles of
$\unicode[STIX]{x1D6FF}_{2}$ indicates that the two capsule interaction leads to self-diffusion effects in a dilute suspension of capsules. The deformed profiles of 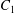 $C_{1}$ (equivalently of
$C_{1}$ (equivalently of 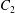 $C_{2}$) in the
$C_{2}$) in the 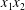 $x_{1}x_{2}$-,
$x_{1}x_{2}$-, 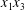 $x_{1}x_{3}$- and
$x_{1}x_{3}$- and 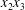 $x_{2}x_{3}$-planes are shown in figure 2(d–f) at time
$x_{2}x_{3}$-planes are shown in figure 2(d–f) at time 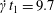 $\dot{\unicode[STIX]{x1D6FE}}t_{1}=9.7$, when the two capsules cross, which we define by
$\dot{\unicode[STIX]{x1D6FE}}t_{1}=9.7$, when the two capsules cross, which we define by  $X_{1}(t_{1})=0$. Figure 2(d,f) shows that there is indeed a thin lubrication film between the two capsules (which corroborates the pressure build-up) and that the two capsules are highly deformed. The global deformation can be assessed through the membrane elastic energy
$X_{1}(t_{1})=0$. Figure 2(d,f) shows that there is indeed a thin lubrication film between the two capsules (which corroborates the pressure build-up) and that the two capsules are highly deformed. The global deformation can be assessed through the membrane elastic energy  $W$ given by (2.9). The value of
$W$ given by (2.9). The value of 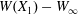 $W(X_{1})-W_{\infty }$, where
$W(X_{1})-W_{\infty }$, where 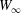 $W_{\infty }$ is the deformation energy of a single capsule, allows us to estimate the intensity of the mechanical interaction between the two capsules. During the close interaction, the two capsules undergo large transient deformation, leading to a peak in
$W_{\infty }$ is the deformation energy of a single capsule, allows us to estimate the intensity of the mechanical interaction between the two capsules. During the close interaction, the two capsules undergo large transient deformation, leading to a peak in 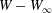 $W-W_{\infty }$ (figure 4b). The separation process leads to some deformation oscillations, until a final steady state is reached, which is identical to the single capsule one, elastic energy wise (figure 4b).
$W-W_{\infty }$ (figure 4b). The separation process leads to some deformation oscillations, until a final steady state is reached, which is identical to the single capsule one, elastic energy wise (figure 4b).
3.2 Minuet motion

Figure 5. Minuet of two capsules (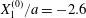 $X_{1}^{(0)}/a=-2.6$,
$X_{1}^{(0)}/a=-2.6$, 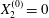 $X_{2}^{(0)}=0$,
$X_{2}^{(0)}=0$, 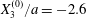 $X_{3}^{(0)}/a=-2.6$,
$X_{3}^{(0)}/a=-2.6$, 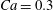 $Ca=0.3$). (a) Three-dimensional view of the trajectory of
$Ca=0.3$). (a) Three-dimensional view of the trajectory of 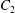 $C_{2}$. (b) Projections of
$C_{2}$. (b) Projections of 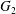 $G_{2}$ trajectories in the
$G_{2}$ trajectories in the 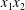 $x_{1}x_{2}$- and
$x_{1}x_{2}$- and 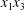 $x_{1}x_{3}$-planes. (c–e)
$x_{1}x_{3}$-planes. (c–e) 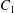 $C_{1}$ profile intersections with the three coordinates planes at times
$C_{1}$ profile intersections with the three coordinates planes at times 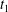 $t_{1}$ and
$t_{1}$ and 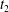 $t_{2}$ when
$t_{2}$ when 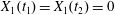 $X_{1}(t_{1})=X_{1}(t_{2})=0$.
$X_{1}(t_{1})=X_{1}(t_{2})=0$.
We now consider the case 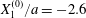 $X_{1}^{(0)}/a=-2.6$,
$X_{1}^{(0)}/a=-2.6$, 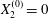 $X_{2}^{(0)}=0$,
$X_{2}^{(0)}=0$, 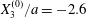 $X_{3}^{(0)}/a=-2.6$,
$X_{3}^{(0)}/a=-2.6$, 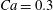 $Ca=0.3$, where capsule
$Ca=0.3$, where capsule 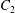 $C_{2}$ is located off the shear plane and can thus move freely in space: this leads to trajectories that are completely different from the ones described above. As in the previous case, the rotation of
$C_{2}$ is located off the shear plane and can thus move freely in space: this leads to trajectories that are completely different from the ones described above. As in the previous case, the rotation of 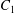 $C_{1}$ displaces
$C_{1}$ displaces  $G_{2}$ along the velocity gradient, so that
$G_{2}$ along the velocity gradient, so that 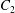 $C_{2}$ is convected towards
$C_{2}$ is convected towards 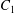 $C_{1}$. The three-dimensional trajectory of
$C_{1}$. The three-dimensional trajectory of  $C_{2}$ is shown in figure 5(a), where the two capsules are shown in their initial positions (movie 2). In order to get a clearer grasp of the process, we analyse the trajectories of the projections of
$C_{2}$ is shown in figure 5(a), where the two capsules are shown in their initial positions (movie 2). In order to get a clearer grasp of the process, we analyse the trajectories of the projections of 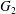 $G_{2}$ in the
$G_{2}$ in the 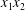 $x_{1}x_{2}$- and
$x_{1}x_{2}$- and  $x_{1}x_{3}$-planes in figure 5(b). As
$x_{1}x_{3}$-planes in figure 5(b). As 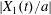 $|X_{1}(t)/a|$ decreases, the pressure increases slightly (figure 4a): this leads to a slight increase in both
$|X_{1}(t)/a|$ decreases, the pressure increases slightly (figure 4a): this leads to a slight increase in both 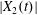 $|X_{2}(t)|$ and
$|X_{2}(t)|$ and 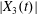 $|X_{3}(t)|$ (figure 5b), which allows enough space for capsule
$|X_{3}(t)|$ (figure 5b), which allows enough space for capsule  $C_{2}$ to pass
$C_{2}$ to pass 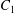 $C_{1}$ by moving around the
$C_{1}$ by moving around the 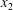 $x_{2}$-axis (insets in figure 5a). Correspondingly, the maximum displacement
$x_{2}$-axis (insets in figure 5a). Correspondingly, the maximum displacement 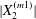 $|X_{2}^{(m1)}|$ is smaller than in the leapfrog situation. Similarly, the velocity difference
$|X_{2}^{(m1)}|$ is smaller than in the leapfrog situation. Similarly, the velocity difference 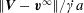 $\Vert \boldsymbol{V}-\boldsymbol{v}^{\infty }\Vert /\dot{\unicode[STIX]{x1D6FE}}a$ remains small while occurring in all three directions, as shown in figure 3. The energy variation
$\Vert \boldsymbol{V}-\boldsymbol{v}^{\infty }\Vert /\dot{\unicode[STIX]{x1D6FE}}a$ remains small while occurring in all three directions, as shown in figure 3. The energy variation 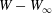 $W-W_{\infty }$ is also very small (figure 4b), which indicates that there is little mechanical interaction between the capsules. This point is further corroborated by the quasi-superposition of the deformed profiles of
$W-W_{\infty }$ is also very small (figure 4b), which indicates that there is little mechanical interaction between the capsules. This point is further corroborated by the quasi-superposition of the deformed profiles of 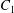 $C_{1}$ at time
$C_{1}$ at time  $t_{1}$ when
$t_{1}$ when  $X_{1}(t_{1})=0$, and when it is alone in the flow (figure 5c–e).
$X_{1}(t_{1})=0$, and when it is alone in the flow (figure 5c–e).
As the capsules separate, the small depression (figure 4a) leads to a negative displacement along the 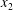 $x_{2}$-axis, which takes
$x_{2}$-axis, which takes  $G_{2}$ into the reverse flow region and entices
$G_{2}$ into the reverse flow region and entices  $C_{2}$ to move back towards
$C_{2}$ to move back towards 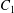 $C_{1}$. The pressure is still negative when the reversal takes place, so that
$C_{1}$. The pressure is still negative when the reversal takes place, so that 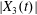 $|X_{3}(t)|$ decreases. As a consequence, there is not enough space for
$|X_{3}(t)|$ decreases. As a consequence, there is not enough space for 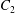 $C_{2}$ to move around
$C_{2}$ to move around 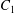 $C_{1}$ in a
$C_{1}$ in a 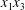 $x_{1}x_{3}$-plane and a sideways leapfrog motion takes place, which is qualitatively similar to the one that occurs in the shear plane, as described in the previous section: there is a significant pressure build-up in the lubrication film, followed by a depression as the capsules part (figure 4a). The pressure variation leads to an increase of
$x_{1}x_{3}$-plane and a sideways leapfrog motion takes place, which is qualitatively similar to the one that occurs in the shear plane, as described in the previous section: there is a significant pressure build-up in the lubrication film, followed by a depression as the capsules part (figure 4a). The pressure variation leads to an increase of 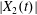 $|X_{2}(t)|$ up to a value
$|X_{2}(t)|$ up to a value  $|X_{2}^{(m2)}|$, which is large enough to allow the further decrease to the final displacement
$|X_{2}^{(m2)}|$, which is large enough to allow the further decrease to the final displacement 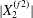 $|X_{2}^{(f2)}|$, without crossing into a reverse flow region. At time
$|X_{2}^{(f2)}|$, without crossing into a reverse flow region. At time 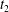 $t_{2}$ when
$t_{2}$ when 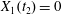 $X_{1}(t_{2})=0$, the two capsules are closer than at time
$X_{1}(t_{2})=0$, the two capsules are closer than at time  $t_{1}$ and thus undergo a transient deformation, as appears in figure 5(a) (inset) and in figure 5(d,e). Correspondingly, the mechanical energy
$t_{1}$ and thus undergo a transient deformation, as appears in figure 5(a) (inset) and in figure 5(d,e). Correspondingly, the mechanical energy 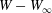 $W-W_{\infty }$ undergoes a transient variation, which, however, is much smaller than the one that occurs when the capsules cross in the shear plane (figure 4b). We deduce that minuet motion is less energy consuming than leapfrog motion.
$W-W_{\infty }$ undergoes a transient variation, which, however, is much smaller than the one that occurs when the capsules cross in the shear plane (figure 4b). We deduce that minuet motion is less energy consuming than leapfrog motion.

Figure 6. Minuet with multiple reversals for 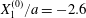 $X_{1}^{(0)}/a=-2.6$,
$X_{1}^{(0)}/a=-2.6$,  $X_{2}^{(0)}=0$,
$X_{2}^{(0)}=0$,  $X_{3}^{(0)}/a=-2.6$,
$X_{3}^{(0)}/a=-2.6$, 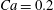 $Ca=0.2$. The instants of close interaction when
$Ca=0.2$. The instants of close interaction when 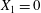 $X_{1}=0$ are denoted
$X_{1}=0$ are denoted 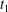 $t_{1}$,
$t_{1}$, 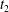 $t_{2}$ and
$t_{2}$ and 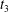 $t_{3}$ in chronological order. (a) Three-dimensional view of the trajectory of
$t_{3}$ in chronological order. (a) Three-dimensional view of the trajectory of  $C_{2}$. (b,c) Projections of
$C_{2}$. (b,c) Projections of 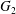 $G_{2}$ trajectories in the
$G_{2}$ trajectories in the 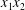 $x_{1}x_{2}$- and
$x_{1}x_{2}$- and 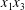 $x_{1}x_{3}$-planes. (d) Three-dimensional profiles at close interaction.
$x_{1}x_{3}$-planes. (d) Three-dimensional profiles at close interaction.
If we now start with the same initial conditions ( $X_{1}^{(0)}/a=-2.6$,
$X_{1}^{(0)}/a=-2.6$, 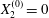 $X_{2}^{(0)}=0$,
$X_{2}^{(0)}=0$, 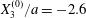 $X_{3}^{(0)}/a=-2.6$) but reduce the capsule deformability by setting
$X_{3}^{(0)}/a=-2.6$) but reduce the capsule deformability by setting  $Ca=0.2$, two reversals occur, as shown in figure 6 (movies 3 and 4). The first reversal is essentially the same as for
$Ca=0.2$, two reversals occur, as shown in figure 6 (movies 3 and 4). The first reversal is essentially the same as for 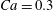 $Ca=0.3$. However, when the capsules cross again at time
$Ca=0.3$. However, when the capsules cross again at time 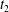 $t_{2}$, there is still enough space to allow crossing around the
$t_{2}$, there is still enough space to allow crossing around the 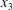 $x_{3}$-axis. Furthermore, the displacement along the
$x_{3}$-axis. Furthermore, the displacement along the  $x_{2}$-axis is still small (
$x_{2}$-axis is still small (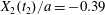 $X_{2}(t_{2})/a=-0.39$), compared to the one observed for
$X_{2}(t_{2})/a=-0.39$), compared to the one observed for  $Ca=0.3$ (
$Ca=0.3$ (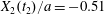 $X_{2}(t_{2})/a=-0.51$), so that the pressure induced trajectory shift forces
$X_{2}(t_{2})/a=-0.51$), so that the pressure induced trajectory shift forces  $G_{2}$ to cross again into the reverse flow region: the capsule is thus convected again towards
$G_{2}$ to cross again into the reverse flow region: the capsule is thus convected again towards  $C_{1}$. During the third crossing, since
$C_{1}$. During the third crossing, since 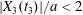 $|X_{3}(t_{3})|/a<2$, the capsule has to do a sideways leapfrog motion that leads to a displacement
$|X_{3}(t_{3})|/a<2$, the capsule has to do a sideways leapfrog motion that leads to a displacement 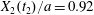 $X_{2}(t_{2})/a=0.92$, that is large enough to accommodate the trajectory shift without changing the flow direction of the capsule: the latter finally goes back in the direction where it came from. Note that, at time
$X_{2}(t_{2})/a=0.92$, that is large enough to accommodate the trajectory shift without changing the flow direction of the capsule: the latter finally goes back in the direction where it came from. Note that, at time 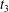 $t_{3}$, the two capsules undergo a significant transient deformation, due to a strong interaction. This phenomenon is unexpected in view of the fairly large initial distance between the capsules.
$t_{3}$, the two capsules undergo a significant transient deformation, due to a strong interaction. This phenomenon is unexpected in view of the fairly large initial distance between the capsules.
4 What factors determine the motion type?
The type of motion (leapfrog or minuet) is determined by the evolution of 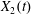 $X_{2}(t)$ after crossing, since it is a change of sign of
$X_{2}(t)$ after crossing, since it is a change of sign of 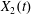 $X_{2}(t)$ that causes reversal of motion. At crossing, the film pressure displaces
$X_{2}(t)$ that causes reversal of motion. At crossing, the film pressure displaces 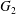 $G_{2}$ along the velocity gradient, to a maximum value
$G_{2}$ along the velocity gradient, to a maximum value 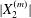 $|X_{2}^{(m)}|$. After crossing, the separation process and the subsequent depression lead to a displacement
$|X_{2}^{(m)}|$. After crossing, the separation process and the subsequent depression lead to a displacement 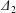 $\unicode[STIX]{x1D6E5}_{2}$ of
$\unicode[STIX]{x1D6E5}_{2}$ of 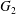 $G_{2}$ back to the
$G_{2}$ back to the  $x_{1}$-axis. For leapfrog motion, the trajectory shift is easily identified as
$x_{1}$-axis. For leapfrog motion, the trajectory shift is easily identified as 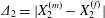 $\unicode[STIX]{x1D6E5}_{2}=|X_{2}^{(m)}-X_{2}^{(f)}|$ (see figure 2b). When reversal occurs, the film pressure decrease also leads to a trajectory shift
$\unicode[STIX]{x1D6E5}_{2}=|X_{2}^{(m)}-X_{2}^{(f)}|$ (see figure 2b). When reversal occurs, the film pressure decrease also leads to a trajectory shift 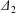 $\unicode[STIX]{x1D6E5}_{2}$, which is difficult to evaluate in a simple fashion. However, since
$\unicode[STIX]{x1D6E5}_{2}$, which is difficult to evaluate in a simple fashion. However, since 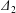 $\unicode[STIX]{x1D6E5}_{2}$ is a consequence of the separation process, we can surmise that it follows an evolution similar to the one found in leapfrog motion in the shear plane, i.e. that it decreases when the capsule separation
$\unicode[STIX]{x1D6E5}_{2}$ is a consequence of the separation process, we can surmise that it follows an evolution similar to the one found in leapfrog motion in the shear plane, i.e. that it decreases when the capsule separation  $|X_{2}^{(0)}|$ and/or
$|X_{2}^{(0)}|$ and/or 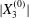 $|X_{3}^{(0)}|$ increase and when the capsule deformability
$|X_{3}^{(0)}|$ increase and when the capsule deformability  $Ca$ increases (Lac et al. Reference Lac, Morel and Barthès-Biesel2007; Lac & Barthès-Biesel Reference Lac and Barthès-Biesel2008; Pranay et al. Reference Pranay, Anekal, Hernandez-Ortiz and Graham2010; Omori et al. Reference Omori, Ishikawa, Imai and Yamaguchi2013; Gires et al. Reference Gires, Srivastav, Misbah, Podgorski and Coupier2014). We conclude that, whenever
$Ca$ increases (Lac et al. Reference Lac, Morel and Barthès-Biesel2007; Lac & Barthès-Biesel Reference Lac and Barthès-Biesel2008; Pranay et al. Reference Pranay, Anekal, Hernandez-Ortiz and Graham2010; Omori et al. Reference Omori, Ishikawa, Imai and Yamaguchi2013; Gires et al. Reference Gires, Srivastav, Misbah, Podgorski and Coupier2014). We conclude that, whenever 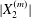 $|X_{2}^{(m)}|$ is less than
$|X_{2}^{(m)}|$ is less than 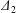 $\unicode[STIX]{x1D6E5}_{2}$, reverse motion is to be expected. The main parameters that determine the values of
$\unicode[STIX]{x1D6E5}_{2}$, reverse motion is to be expected. The main parameters that determine the values of 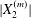 $|X_{2}^{(m)}|$ and of
$|X_{2}^{(m)}|$ and of 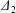 $\unicode[STIX]{x1D6E5}_{2}$, are the initial capsule separation
$\unicode[STIX]{x1D6E5}_{2}$, are the initial capsule separation 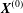 $\boldsymbol{X}^{(0)}$ and the capillary number
$\boldsymbol{X}^{(0)}$ and the capillary number  $Ca$. We now study their influence separately.
$Ca$. We now study their influence separately.
4.1 Effect of the initial capsule separation  $\boldsymbol{X}^{(0)}$
$\boldsymbol{X}^{(0)}$

Figure 7. Effect of the initial position 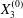 $X_{3}^{(0)}$ on the capsule trajectory for
$X_{3}^{(0)}$ on the capsule trajectory for  $Ca=0.3$,
$Ca=0.3$, 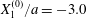 $X_{1}^{(0)}/a=-3.0$ and
$X_{1}^{(0)}/a=-3.0$ and 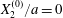 $X_{2}^{(0)}/a=0$. Projections of
$X_{2}^{(0)}/a=0$. Projections of 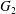 $G_{2}$ trajectories in the
$G_{2}$ trajectories in the  $x_{1}x_{2}$-plane (a) and in the
$x_{1}x_{2}$-plane (a) and in the 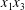 $x_{1}x_{3}$-plane (b). When
$x_{1}x_{3}$-plane (b). When 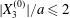 $|X_{3}^{(0)}|/a\leqslant 2$, capsule
$|X_{3}^{(0)}|/a\leqslant 2$, capsule 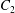 $C_{2}$ has not enough room to move around
$C_{2}$ has not enough room to move around 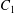 $C_{1}$: it overpasses it with a sideways leapfrog motion.
$C_{1}$: it overpasses it with a sideways leapfrog motion.
The effect of the initial offset  $|X_{3}^{(0)}|$ from the shear plane is shown for
$|X_{3}^{(0)}|$ from the shear plane is shown for 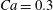 $Ca=0.3$,
$Ca=0.3$, 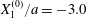 $X_{1}^{(0)}/a=-3.0$ and
$X_{1}^{(0)}/a=-3.0$ and 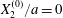 $X_{2}^{(0)}/a=0$ in figure 7. When
$X_{2}^{(0)}/a=0$ in figure 7. When  $|X_{3}^{(0)}|$ is small (e.g.
$|X_{3}^{(0)}|$ is small (e.g.  $|X_{3}^{(0)}/a|\leqslant 2$), the situation is close to the one when the two capsules are in the same shear plane. Correspondingly, they undergo a sideways leapfrog motion with a displacement
$|X_{3}^{(0)}/a|\leqslant 2$), the situation is close to the one when the two capsules are in the same shear plane. Correspondingly, they undergo a sideways leapfrog motion with a displacement 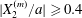 $|X_{2}^{(m)}/a|\geqslant 0.4$, which is large enough to allow direct crossing (figure 7a). For a larger offset
$|X_{2}^{(m)}/a|\geqslant 0.4$, which is large enough to allow direct crossing (figure 7a). For a larger offset 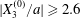 $|X_{3}^{(0)}/a|\geqslant 2.6$,
$|X_{3}^{(0)}/a|\geqslant 2.6$, 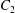 $C_{2}$ has room to move around
$C_{2}$ has room to move around 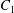 $C_{1}$ in an
$C_{1}$ in an 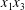 $x_{1}x_{3}$-plane: then the displacement
$x_{1}x_{3}$-plane: then the displacement 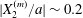 $|X_{2}^{(m)}/a|\sim 0.2$ is small (figure 7a), and thus reversal motion occurs during separation. As
$|X_{2}^{(m)}/a|\sim 0.2$ is small (figure 7a), and thus reversal motion occurs during separation. As 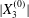 $|X_{3}^{(0)}|$ increases, the influence of
$|X_{3}^{(0)}|$ increases, the influence of 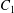 $C_{1}$ decreases and the two capsules have almost no relative velocity. The motion shown in figure 7 for
$C_{1}$ decreases and the two capsules have almost no relative velocity. The motion shown in figure 7 for 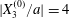 $|X_{3}^{(0)}/a|=4$ is near the limit of what can be reasonably computed: indeed, the capsule reaches
$|X_{3}^{(0)}/a|=4$ is near the limit of what can be reasonably computed: indeed, the capsule reaches 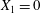 $X_{1}=0$ at time
$X_{1}=0$ at time  $\dot{\unicode[STIX]{x1D6FE}}t_{1}=50$ at the first crossing, and at time
$\dot{\unicode[STIX]{x1D6FE}}t_{1}=50$ at the first crossing, and at time  $\dot{\unicode[STIX]{x1D6FE}}t_{2}=266$ at the second crossing. We conclude that the minuet motion is slow.
$\dot{\unicode[STIX]{x1D6FE}}t_{2}=266$ at the second crossing. We conclude that the minuet motion is slow.

Figure 8. Effect of the initial position 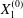 $X_{1}^{(0)}$ on the capsule trajectory for
$X_{1}^{(0)}$ on the capsule trajectory for 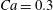 $Ca=0.3$,
$Ca=0.3$,  $X_{2}^{(0)}/a=0$ and
$X_{2}^{(0)}/a=0$ and  $X_{3}^{(0)}/a=-2.6$. Projections of
$X_{3}^{(0)}/a=-2.6$. Projections of 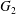 $G_{2}$ trajectories in the
$G_{2}$ trajectories in the 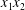 $x_{1}x_{2}$-plane (a) and in the
$x_{1}x_{2}$-plane (a) and in the 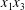 $x_{1}x_{3}$-plane (b). When
$x_{1}x_{3}$-plane (b). When 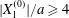 $|X_{1}^{(0)}|/a\geqslant 4$, capsule
$|X_{1}^{(0)}|/a\geqslant 4$, capsule 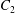 $C_{2}$ has moved sufficiently across the streamlines that it can overpass
$C_{2}$ has moved sufficiently across the streamlines that it can overpass 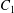 $C_{1}$ with a sideways leapfrog motion.
$C_{1}$ with a sideways leapfrog motion.
We now turn to the effect of the initial distance 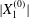 $|X_{1}^{(0)}|$ on the trajectory of
$|X_{1}^{(0)}|$ on the trajectory of 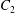 $C_{2}$, as shown in figure 8 for
$C_{2}$, as shown in figure 8 for 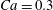 $Ca=0.3$,
$Ca=0.3$, 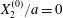 $X_{2}^{(0)}/a=0$ and
$X_{2}^{(0)}/a=0$ and 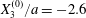 $X_{3}^{(0)}/a=-2.6$. Note that, since
$X_{3}^{(0)}/a=-2.6$. Note that, since 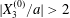 $|X_{3}^{(0)}/a|>2$,
$|X_{3}^{(0)}/a|>2$,  $C_{2}$ has room to move around
$C_{2}$ has room to move around 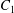 $C_{1}$ in an
$C_{1}$ in an 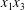 $x_{1}x_{3}$-plane. However, the far field perturbation created by
$x_{1}x_{3}$-plane. However, the far field perturbation created by 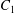 $C_{1}$ is a stresslet, which varies as the square of the inverse distance
$C_{1}$ is a stresslet, which varies as the square of the inverse distance 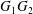 $G_{1}G_{2}$. It is this perturbation that displaces
$G_{1}G_{2}$. It is this perturbation that displaces 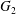 $G_{2}$ along the
$G_{2}$ along the 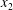 $x_{2}$-axis and gives
$x_{2}$-axis and gives 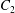 $C_{2}$ the small relative approach velocity, which leads to crossing. This perturbation velocity varies as
$C_{2}$ the small relative approach velocity, which leads to crossing. This perturbation velocity varies as 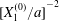 $[X_{1}^{(0)}/a]^{-2}$ when
$[X_{1}^{(0)}/a]^{-2}$ when 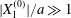 $|X_{1}^{(0)}|/a\gg 1$ (
$|X_{1}^{(0)}|/a\gg 1$ ( $|X_{1}^{(0)}|/a>4$ in this particular case). Even though it is small, its prolonged effect over a long time leads to a significant
$|X_{1}^{(0)}|/a>4$ in this particular case). Even though it is small, its prolonged effect over a long time leads to a significant 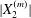 $|X_{2}^{(m)}|$ displacement and thus to a sideways leapfrog motion. Note that the initial position
$|X_{2}^{(m)}|$ displacement and thus to a sideways leapfrog motion. Note that the initial position 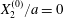 $X_{2}^{(0)}/a=0$ is unstable when the capsules interact. However, when the initial distance
$X_{2}^{(0)}/a=0$ is unstable when the capsules interact. However, when the initial distance 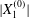 $|X_{1}^{(0)}|$ becomes of order
$|X_{1}^{(0)}|$ becomes of order  $a$ (e.g.
$a$ (e.g. 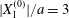 $|X_{1}^{(0)}|/a=3$), the displacement
$|X_{1}^{(0)}|/a=3$), the displacement 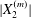 $|X_{2}^{(m)}|$ has no time to build up and remains small: then reversal occurs.
$|X_{2}^{(m)}|$ has no time to build up and remains small: then reversal occurs.
Similar situations of capsule interaction have been considered by Lac & Barthès-Biesel (Reference Lac and Barthès-Biesel2008), who did not report any motion reversal, even when they studied three-dimensional motions with non-zero values of 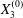 $X_{3}^{(0)}$. This is due to the fact that they started with
$X_{3}^{(0)}$. This is due to the fact that they started with  $X_{2}^{(0)}/a\geqslant 0.5$ and
$X_{2}^{(0)}/a\geqslant 0.5$ and 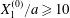 $X_{1}^{(0)}/a\geqslant 10$, values which were too large for minuet to occur.
$X_{1}^{(0)}/a\geqslant 10$, values which were too large for minuet to occur.
4.2 Effect of capsule deformability

Figure 9. Phase diagrams for motion type: (a) motion type as a function of  $Ca$ and
$Ca$ and 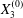 $X_{3}^{(0)}$ for
$X_{3}^{(0)}$ for 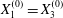 $X_{1}^{(0)}=X_{3}^{(0)}$ and
$X_{1}^{(0)}=X_{3}^{(0)}$ and 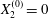 $X_{2}^{(0)}=0$. The points represent the positions of
$X_{2}^{(0)}=0$. The points represent the positions of 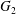 $G_{2}$ at rest:
$G_{2}$ at rest:  $\times$ one oscillation,
$\times$ one oscillation, 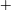 $+$ two oscillations, ♦ three oscillations. (b) Motion type as a function of
$+$ two oscillations, ♦ three oscillations. (b) Motion type as a function of  $Ca$ and
$Ca$ and  $X_{2}^{(0)}$ for
$X_{2}^{(0)}$ for 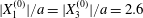 $|X_{1}^{(0)}|/a=|X_{3}^{(0)}|/a=2.6$.
$|X_{1}^{(0)}|/a=|X_{3}^{(0)}|/a=2.6$.
Under given flow conditions, the capsule deformability is accounted for by the capillary number  $Ca$ and increases with it. Some global results are presented in the form of phase diagrams. For
$Ca$ and increases with it. Some global results are presented in the form of phase diagrams. For 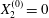 $X_{2}^{(0)}=0$ and
$X_{2}^{(0)}=0$ and 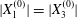 $|X_{1}^{(0)}|=|X_{3}^{(0)}|$, the effect of varying the initial capsule separation and deformability is shown in figure 9(a). Minuet thus occurs approximately for
$|X_{1}^{(0)}|=|X_{3}^{(0)}|$, the effect of varying the initial capsule separation and deformability is shown in figure 9(a). Minuet thus occurs approximately for 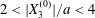 $2<|X_{3}^{(0)}|/a<4$. For
$2<|X_{3}^{(0)}|/a<4$. For  $|X_{3}^{(0)}|/a>4\sim 5$, the capsule separation is so large that the relative velocity is very small and the capsule doublet configuration remains essentially stationary. The effect of
$|X_{3}^{(0)}|/a>4\sim 5$, the capsule separation is so large that the relative velocity is very small and the capsule doublet configuration remains essentially stationary. The effect of  $Ca$ is complex: for a typical separation
$Ca$ is complex: for a typical separation 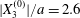 $|X_{3}^{(0)}|/a=2.6$ and up to
$|X_{3}^{(0)}|/a=2.6$ and up to 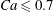 $Ca\leqslant 0.7$, a minuet takes place with one reversal for moderate values of deformability (
$Ca\leqslant 0.7$, a minuet takes place with one reversal for moderate values of deformability ( $0.2<Ca<0.7$) or two (or more) reversals when
$0.2<Ca<0.7$) or two (or more) reversals when 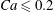 $Ca\leqslant 0.2$. This transition from one to two reversals when
$Ca\leqslant 0.2$. This transition from one to two reversals when  $Ca$ is reduced has been illustrated in § 3.2. However, for large capsule deformability (
$Ca$ is reduced has been illustrated in § 3.2. However, for large capsule deformability (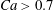 $Ca>0.7$), no motion reversal occurs: the capsules are so deformed and tilted towards the flow direction, that, when they overpass, their trajectory perturbation is small. The effect of
$Ca>0.7$), no motion reversal occurs: the capsules are so deformed and tilted towards the flow direction, that, when they overpass, their trajectory perturbation is small. The effect of  $X_{2}^{(0)}$ is shown in figure 9(b) for the typical case
$X_{2}^{(0)}$ is shown in figure 9(b) for the typical case 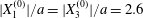 $|X_{1}^{(0)}|/a=|X_{3}^{(0)}|/a=2.6$. Minuet occurs only for small values of
$|X_{1}^{(0)}|/a=|X_{3}^{(0)}|/a=2.6$. Minuet occurs only for small values of 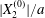 $|X_{2}^{(0)}|/a$ and moderate
$|X_{2}^{(0)}|/a$ and moderate  $Ca$, i.e. for small relative velocities between two capsules with moderate deformability. This limited range of minuet motion explains why it had not been detected before.
$Ca$, i.e. for small relative velocities between two capsules with moderate deformability. This limited range of minuet motion explains why it had not been detected before.
Note that the inherent deformability of a capsule, even when  $Ca$ is very small, makes it different from a rigid sphere. Consequently, it is impossible to find permanent capsule doublets like those predicted by Batchelor & Green (Reference Batchelor and Green1972b) for two spheres freely suspended in simple shear flow: indeed, such doublets can occur only for perfect spheres, as pointed out by the authors.
$Ca$ is very small, makes it different from a rigid sphere. Consequently, it is impossible to find permanent capsule doublets like those predicted by Batchelor & Green (Reference Batchelor and Green1972b) for two spheres freely suspended in simple shear flow: indeed, such doublets can occur only for perfect spheres, as pointed out by the authors.
4.3 Region of minuet motion

Figure 10. Domain of doublet formation around capsule 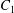 $C_{1}$ for
$C_{1}$ for 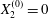 $X_{2}^{(0)}=0$,
$X_{2}^{(0)}=0$, 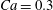 $Ca=0.3$ and a NH membrane. The sphere of radius
$Ca=0.3$ and a NH membrane. The sphere of radius  $2a$ is a steric exclusion area, while the grey zone between the spheres of radii
$2a$ is a steric exclusion area, while the grey zone between the spheres of radii 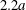 $2.2a$ and
$2.2a$ and 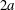 $2a$ is an exclusion region, that leaves a space
$2a$ is an exclusion region, that leaves a space 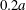 $0.2a$ between the two capsules. The points represent the positions of
$0.2a$ between the two capsules. The points represent the positions of 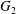 $G_{2}$ at rest, and the symbols indicate the motion type:
$G_{2}$ at rest, and the symbols indicate the motion type:  $\times$ minuet, ▫ leapfrog, ♢ steady doublet. The position of the boundary between the two domains for
$\times$ minuet, ▫ leapfrog, ♢ steady doublet. The position of the boundary between the two domains for 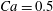 $Ca=0.5$ is indicated by a dash line.
$Ca=0.5$ is indicated by a dash line.
The domain around 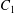 $C_{1}$, where long term doublets are formed, is illustrated in figure 10 for
$C_{1}$, where long term doublets are formed, is illustrated in figure 10 for  $Ca=0.3$. The sphere of radius
$Ca=0.3$. The sphere of radius 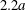 $2.2a$ centred on
$2.2a$ centred on 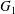 $G_{1}$ is an exclusion region, that leaves a space
$G_{1}$ is an exclusion region, that leaves a space 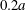 $0.2a$ between the two capsules. When
$0.2a$ between the two capsules. When 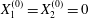 $X_{1}^{(0)}=X_{2}^{(0)}=0$, the capsule doublet separated by
$X_{1}^{(0)}=X_{2}^{(0)}=0$, the capsule doublet separated by 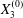 $X_{3}^{(0)}$, remains stationary. Whenever the centre of capsule
$X_{3}^{(0)}$, remains stationary. Whenever the centre of capsule 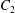 $C_{2}$ is located in the yellow area, the two capsules will cross once (leapfrog motion) and separate. In the green area, the two capsules will remain close and oscillate a few times before eventually separating. For
$C_{2}$ is located in the yellow area, the two capsules will cross once (leapfrog motion) and separate. In the green area, the two capsules will remain close and oscillate a few times before eventually separating. For 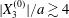 $|X_{3}^{(0)}|/a\gtrsim 4$, the interaction becomes weak, so that the doublet configuration remains essentially stationary. The minuet domain shown in figure 10 is in fact three-dimensional and extends in the
$|X_{3}^{(0)}|/a\gtrsim 4$, the interaction becomes weak, so that the doublet configuration remains essentially stationary. The minuet domain shown in figure 10 is in fact three-dimensional and extends in the 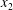 $x_{2}$-direction over a small distance of order 0.06a for
$x_{2}$-direction over a small distance of order 0.06a for 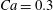 $Ca=0.3$ (see figure 9b). When
$Ca=0.3$ (see figure 9b). When  $Ca$ is decreased, the boundary between leapfrog and minuet motions does not change appreciatively, but the thickness of the three-dimensional minuet domain increases. Conversely, as shown in figure 10, when
$Ca$ is decreased, the boundary between leapfrog and minuet motions does not change appreciatively, but the thickness of the three-dimensional minuet domain increases. Conversely, as shown in figure 10, when  $Ca$ increases, the boundary is tilted towards the
$Ca$ increases, the boundary is tilted towards the 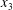 $x_{3}$-axis and the minuet domain thickness decreases. Note that for
$x_{3}$-axis and the minuet domain thickness decreases. Note that for 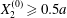 $X_{2}^{(0)}\geqslant 0.5a$, the whole region would be yellow (apart from the exclusion area).
$X_{2}^{(0)}\geqslant 0.5a$, the whole region would be yellow (apart from the exclusion area).
An important consequence of the minuet motion is linked to the fact that it tends to push together two capsules that were initially distant and not expected to interact much. This point is illustrated in figure 6 where the initial separation 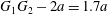 $G_{1}G_{2}-2a=1.7a$ is decreased during crossing to a film with thickness approximately
$G_{1}G_{2}-2a=1.7a$ is decreased during crossing to a film with thickness approximately 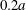 $0.2a$, which is thin enough to lead to potential physico-chemical interactions or damage.
$0.2a$, which is thin enough to lead to potential physico-chemical interactions or damage.
4.4 Effect of the membrane constitutive equation

Figure 11. Interaction process of two capsules with a NH membrane or a SK membrane for 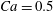 $Ca=0.5$,
$Ca=0.5$, 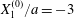 $X_{1}^{(0)}/a=-3$,
$X_{1}^{(0)}/a=-3$, 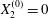 $X_{2}^{(0)}=0$,
$X_{2}^{(0)}=0$, 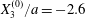 $X_{3}^{(0)}/a=-2.6$. (a) The NH capsule does a sideways leapfrog motion, while the SK capsule does a motion reversal. (b) Deformed profiles of the capsule
$X_{3}^{(0)}/a=-2.6$. (a) The NH capsule does a sideways leapfrog motion, while the SK capsule does a motion reversal. (b) Deformed profiles of the capsule 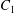 $C_{1}$ at time
$C_{1}$ at time 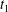 $t_{1}$ defined by
$t_{1}$ defined by 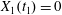 $X_{1}(t_{1})=0$.
$X_{1}(t_{1})=0$.
It is of interest to assess the influence of the wall constitutive law, as all the above results have been obtained for a neo-Hookean membrane. In particular, it is possible to assume that the principal tensions and elongations are related by the Skalak law (SK) (Skalak et al. Reference Skalak, Tozeren, Zarda and Chien1973), which reads
 $$\begin{eqnarray}T_{1}=\frac{G_{s}}{\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D706}_{2}}[\unicode[STIX]{x1D706}_{1}^{2}(\unicode[STIX]{x1D706}_{1}^{2}-1)+C\unicode[STIX]{x1D706}_{1}^{2}\unicode[STIX]{x1D706}_{2}^{2}(\unicode[STIX]{x1D706}_{1}^{2}\unicode[STIX]{x1D706}_{2}^{2}-1)].\end{eqnarray}$$
$$\begin{eqnarray}T_{1}=\frac{G_{s}}{\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D706}_{2}}[\unicode[STIX]{x1D706}_{1}^{2}(\unicode[STIX]{x1D706}_{1}^{2}-1)+C\unicode[STIX]{x1D706}_{1}^{2}\unicode[STIX]{x1D706}_{2}^{2}(\unicode[STIX]{x1D706}_{1}^{2}\unicode[STIX]{x1D706}_{2}^{2}-1)].\end{eqnarray}$$ The surface shear elastic modulus is  $G_{s}$ and the area dilation modulus is given by
$G_{s}$ and the area dilation modulus is given by 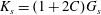 $K_{s}=(1+2C)G_{s}$. The two laws (2.8) and (4.1) predict the same small deformation behaviour for
$K_{s}=(1+2C)G_{s}$. The two laws (2.8) and (4.1) predict the same small deformation behaviour for  $C=1$, but for large deformations, the NH law is strain softening, whereas SK law is strain hardening (Barthès-Biesel, Diaz & Dhenin Reference Barthès-Biesel, Diaz and Dhenin2002). Correspondingly, for the same value of
$C=1$, but for large deformations, the NH law is strain softening, whereas SK law is strain hardening (Barthès-Biesel, Diaz & Dhenin Reference Barthès-Biesel, Diaz and Dhenin2002). Correspondingly, for the same value of  $Ca$, the deformation of a single capsule in simple shear flow is larger for a NH membrane than for a SK one (Barthès-Biesel Reference Barthès-Biesel2016).
$Ca$, the deformation of a single capsule in simple shear flow is larger for a NH membrane than for a SK one (Barthès-Biesel Reference Barthès-Biesel2016).
We can then expect that the transition between a leapfrog and a minuet motion will happen for values of  $Ca$ that will be different for capsules with SK or NH membranes. In order to verify this prediction, we model the interaction of two capsules enclosed either by a SK membrane (
$Ca$ that will be different for capsules with SK or NH membranes. In order to verify this prediction, we model the interaction of two capsules enclosed either by a SK membrane ( $C=1$) or a NH membrane, in the case
$C=1$) or a NH membrane, in the case  $X_{1}^{(0)}/a=-3.0$,
$X_{1}^{(0)}/a=-3.0$,  $X_{2}^{(0)}=0$,
$X_{2}^{(0)}=0$,  $X_{3}^{(0)}/a=-2.6$ and
$X_{3}^{(0)}/a=-2.6$ and 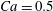 $Ca=0.5$. As shown in figure 11(a), the NH capsules do a sideways leapfrog motion whereas the SK capsules undergo one oscillation and reverse their direction of motion. The explanation for this difference of behaviour is linked to the fact that the NH capsule is more deformed than the SK one (figure 11b), and that its trajectory displacement
$Ca=0.5$. As shown in figure 11(a), the NH capsules do a sideways leapfrog motion whereas the SK capsules undergo one oscillation and reverse their direction of motion. The explanation for this difference of behaviour is linked to the fact that the NH capsule is more deformed than the SK one (figure 11b), and that its trajectory displacement 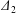 $\unicode[STIX]{x1D6E5}_{2}$ is thus small enough to prevent it from going into the reverse flow region.
$\unicode[STIX]{x1D6E5}_{2}$ is thus small enough to prevent it from going into the reverse flow region.
5 Global effects: trajectory shift and doublet duration
5.1 Trajectory shift
When two capsules with a NH membrane are in the same shear plane ( $X_{3}^{(0)}/a=0$), it is a well-established fact that, after crossing, the two capsules are irreversibly displaced from their initial trajectory: for a given value of
$X_{3}^{(0)}/a=0$), it is a well-established fact that, after crossing, the two capsules are irreversibly displaced from their initial trajectory: for a given value of  $Ca$, the trajectory shift
$Ca$, the trajectory shift 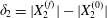 $\unicode[STIX]{x1D6FF}_{2}=|X_{2}^{(f)}|-|X_{2}^{(0)}|$ is maximum for
$\unicode[STIX]{x1D6FF}_{2}=|X_{2}^{(f)}|-|X_{2}^{(0)}|$ is maximum for 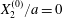 $X_{2}^{(0)}/a=0$, decreases when
$X_{2}^{(0)}/a=0$, decreases when 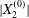 $|X_{2}^{(0)}|$ increases and becomes almost zero for
$|X_{2}^{(0)}|$ increases and becomes almost zero for 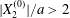 $|X_{2}^{(0)}|/a>2$ (Lac & Barthès-Biesel Reference Lac and Barthès-Biesel2008; Pranay et al. Reference Pranay, Anekal, Hernandez-Ortiz and Graham2010; Omori et al. Reference Omori, Ishikawa, Imai and Yamaguchi2013; Gires et al. Reference Gires, Srivastav, Misbah, Podgorski and Coupier2014). The effect of
$|X_{2}^{(0)}|/a>2$ (Lac & Barthès-Biesel Reference Lac and Barthès-Biesel2008; Pranay et al. Reference Pranay, Anekal, Hernandez-Ortiz and Graham2010; Omori et al. Reference Omori, Ishikawa, Imai and Yamaguchi2013; Gires et al. Reference Gires, Srivastav, Misbah, Podgorski and Coupier2014). The effect of 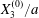 $X_{3}^{(0)}/a$ is mostly reported for the case
$X_{3}^{(0)}/a$ is mostly reported for the case 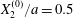 $X_{2}^{(0)}/a=0.5$: then
$X_{2}^{(0)}/a=0.5$: then 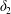 $\unicode[STIX]{x1D6FF}_{2}$ is maximum for
$\unicode[STIX]{x1D6FF}_{2}$ is maximum for 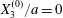 $X_{3}^{(0)}/a=0$, decreasing to almost zero for
$X_{3}^{(0)}/a=0$, decreasing to almost zero for 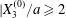 $|X_{3}^{(0)}/a\geqslant 2$ (Lac & Barthès-Biesel Reference Lac and Barthès-Biesel2008; Gires et al. Reference Gires, Srivastav, Misbah, Podgorski and Coupier2014). The trajectory shift along the vorticity direction
$|X_{3}^{(0)}/a\geqslant 2$ (Lac & Barthès-Biesel Reference Lac and Barthès-Biesel2008; Gires et al. Reference Gires, Srivastav, Misbah, Podgorski and Coupier2014). The trajectory shift along the vorticity direction  $\unicode[STIX]{x1D6FF}_{3}=|X_{3}^{(f)}|-|X_{3}^{(0)}|$ is small and less than
$\unicode[STIX]{x1D6FF}_{3}=|X_{3}^{(f)}|-|X_{3}^{(0)}|$ is small and less than 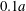 $0.1a$ (see also figure 15). The effect of
$0.1a$ (see also figure 15). The effect of  $Ca$ is small and does not change the findings. The influence of the membrane constitutive law on the leapfrog motion in the shear plane was studied by Pranay et al. (Reference Pranay, Anekal, Hernandez-Ortiz and Graham2010), who compared the effect of a NH or SK law (
$Ca$ is small and does not change the findings. The influence of the membrane constitutive law on the leapfrog motion in the shear plane was studied by Pranay et al. (Reference Pranay, Anekal, Hernandez-Ortiz and Graham2010), who compared the effect of a NH or SK law (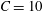 $C=10$) on the trajectory shift
$C=10$) on the trajectory shift  $\unicode[STIX]{x1D6FF}_{2}$. They found that, for the same
$\unicode[STIX]{x1D6FF}_{2}$. They found that, for the same  $Ca$,
$Ca$, 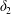 $\unicode[STIX]{x1D6FF}_{2}$ is larger for a SK law than for a NH one: this is due to the high apparent rigidity of the SK law, linked to a high value of the area dilation modulus.
$\unicode[STIX]{x1D6FF}_{2}$ is larger for a SK law than for a NH one: this is due to the high apparent rigidity of the SK law, linked to a high value of the area dilation modulus.

Figure 12. Irreversible trajectory shifts 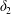 $\unicode[STIX]{x1D6FF}_{2}$ and
$\unicode[STIX]{x1D6FF}_{2}$ and 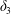 $\unicode[STIX]{x1D6FF}_{3}$, computed at
$\unicode[STIX]{x1D6FF}_{3}$, computed at  $|X_{1}^{(f)}|/a=10$, as a function of
$|X_{1}^{(f)}|/a=10$, as a function of 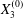 $X_{3}^{(0)}$ (
$X_{3}^{(0)}$ (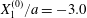 $X_{1}^{(0)}/a=-3.0$,
$X_{1}^{(0)}/a=-3.0$,  $X_{2}^{(0)}=0$,
$X_{2}^{(0)}=0$, 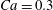 $Ca=0.3$). Open symbols correspond to leapfrog motion, filled ones to minuet motion. The dash-dot line corresponds to the results of Lac & Barthès-Biesel (Reference Lac and Barthès-Biesel2008), obtained for
$Ca=0.3$). Open symbols correspond to leapfrog motion, filled ones to minuet motion. The dash-dot line corresponds to the results of Lac & Barthès-Biesel (Reference Lac and Barthès-Biesel2008), obtained for 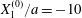 $X_{1}^{(0)}/a=-10$,
$X_{1}^{(0)}/a=-10$, 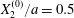 $X_{2}^{(0)}/a=0.5$ and
$X_{2}^{(0)}/a=0.5$ and 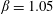 $\unicode[STIX]{x1D6FD}=1.05$.
$\unicode[STIX]{x1D6FD}=1.05$.
The new results for 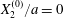 $X_{2}^{(0)}/a=0$ are illustrated for
$X_{2}^{(0)}/a=0$ are illustrated for 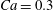 $Ca=0.3$ in figure 12, where they are compared with the results of Lac & Barthès-Biesel (Reference Lac and Barthès-Biesel2008), obtained for
$Ca=0.3$ in figure 12, where they are compared with the results of Lac & Barthès-Biesel (Reference Lac and Barthès-Biesel2008), obtained for 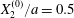 $X_{2}^{(0)}/a=0.5$. For
$X_{2}^{(0)}/a=0.5$. For  $X_{3}^{(0)}/a\leqslant 2$ when a leapfrog motion occurs, the shift
$X_{3}^{(0)}/a\leqslant 2$ when a leapfrog motion occurs, the shift 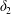 $\unicode[STIX]{x1D6FF}_{2}$ decreases with
$\unicode[STIX]{x1D6FF}_{2}$ decreases with 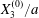 $X_{3}^{(0)}/a$ and is approximately 50 % larger for
$X_{3}^{(0)}/a$ and is approximately 50 % larger for 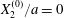 $X_{2}^{(0)}/a=0$ than for
$X_{2}^{(0)}/a=0$ than for 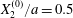 $X_{2}^{(0)}/a=0.5$ (figure 12a): this is in agreement with the previously reported evolution of
$X_{2}^{(0)}/a=0.5$ (figure 12a): this is in agreement with the previously reported evolution of  $\unicode[STIX]{x1D6FF}_{2}$ with
$\unicode[STIX]{x1D6FF}_{2}$ with  $X_{2}^{(0)}/a$ and
$X_{2}^{(0)}/a$ and 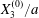 $X_{3}^{(0)}/a$. However, when the doublet motion evolves from leapfrog to minuet, a bifurcation takes place for
$X_{3}^{(0)}/a$. However, when the doublet motion evolves from leapfrog to minuet, a bifurcation takes place for 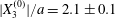 $|X_{3}^{(0)}|/a=2.1\pm 0.1$:
$|X_{3}^{(0)}|/a=2.1\pm 0.1$: 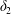 $\unicode[STIX]{x1D6FF}_{2}$ jumps to values that are approximately one order of magnitude larger than the ones that would be expected from the previous
$\unicode[STIX]{x1D6FF}_{2}$ jumps to values that are approximately one order of magnitude larger than the ones that would be expected from the previous  $X_{2}^{(0)}/a=0.5$ results or from the prolongation of the leapfrog curve for
$X_{2}^{(0)}/a=0.5$ results or from the prolongation of the leapfrog curve for  $\unicode[STIX]{x1D6FF}_{2}$.
$\unicode[STIX]{x1D6FF}_{2}$.
Similarly, whereas the shift 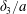 $\unicode[STIX]{x1D6FF}_{3}/a$ remains small during the leapfrog motion, it becomes large and negative for
$\unicode[STIX]{x1D6FF}_{3}/a$ remains small during the leapfrog motion, it becomes large and negative for 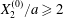 $X_{2}^{(0)}/a\geqslant 2$ (figure 12b). This means that, at the end of the interaction process, the capsule
$X_{2}^{(0)}/a\geqslant 2$ (figure 12b). This means that, at the end of the interaction process, the capsule 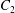 $C_{2}$ is nearer the shear plane
$C_{2}$ is nearer the shear plane 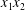 $x_{1}x_{2}$ than when the flow started. The minuet motion thus leads to a shift
$x_{1}x_{2}$ than when the flow started. The minuet motion thus leads to a shift  $\unicode[STIX]{x1D6FF}_{3}$ along the vorticity direction, which tends to reduce the initial distance between the two capsules, in opposition to a diffusive effect. But since the capsule separation in the
$\unicode[STIX]{x1D6FF}_{3}$ along the vorticity direction, which tends to reduce the initial distance between the two capsules, in opposition to a diffusive effect. But since the capsule separation in the 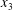 $x_{3}$-direction is reduced, a sideways leapfrog motion takes place, with a resulting large value of
$x_{3}$-direction is reduced, a sideways leapfrog motion takes place, with a resulting large value of  $\unicode[STIX]{x1D6FF}_{2}$, and thus diffusive effects along the shear gradient direction. Decreasing
$\unicode[STIX]{x1D6FF}_{2}$, and thus diffusive effects along the shear gradient direction. Decreasing  $Ca$ does not change much the above results. However, when the capsule deformability increases, the bifurcation occurs for increasingly large values of
$Ca$ does not change much the above results. However, when the capsule deformability increases, the bifurcation occurs for increasingly large values of  $|X_{3}^{(0)}|/a$ and is difficult to compute as the minuet becomes very slow (see § 5.2).
$|X_{3}^{(0)}|/a$ and is difficult to compute as the minuet becomes very slow (see § 5.2).
The influence of the membrane law is shown in figure 13: the SK capsule undergoes a leapfrog motion for 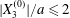 $|X_{3}^{(0)}|/a\leqslant 2$ and then makes a minuet for
$|X_{3}^{(0)}|/a\leqslant 2$ and then makes a minuet for 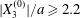 $|X_{3}^{(0)}|/a\geqslant 2.2$. The evolutions of
$|X_{3}^{(0)}|/a\geqslant 2.2$. The evolutions of 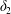 $\unicode[STIX]{x1D6FF}_{2}$ are almost superimposed for a NH membrane (
$\unicode[STIX]{x1D6FF}_{2}$ are almost superimposed for a NH membrane (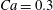 $Ca=0.3$) and for a SK membrane (
$Ca=0.3$) and for a SK membrane (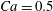 $Ca=0.5$). When the SK capsule deformability increases to
$Ca=0.5$). When the SK capsule deformability increases to 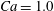 $Ca=1.0$, the transition between leapfrog and minuet motions occurs further away, around
$Ca=1.0$, the transition between leapfrog and minuet motions occurs further away, around  $|X_{3}^{(0)}|/a\sim 3.5$. We can then conclude that, indeed, the effect of a strain hardening membrane would just be to shift the results to larger values of
$|X_{3}^{(0)}|/a\sim 3.5$. We can then conclude that, indeed, the effect of a strain hardening membrane would just be to shift the results to larger values of  $Ca$, without changing the essence of the interaction process.
$Ca$, without changing the essence of the interaction process.

Figure 13. Trajectory shift 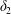 $\unicode[STIX]{x1D6FF}_{2}$ as a function of
$\unicode[STIX]{x1D6FF}_{2}$ as a function of 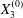 $X_{3}^{(0)}$ for different membranes constitutive laws (
$X_{3}^{(0)}$ for different membranes constitutive laws (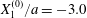 $X_{1}^{(0)}/a=-3.0$,
$X_{1}^{(0)}/a=-3.0$,  $X_{2}^{(0)}=0$). The solid line corresponds to a neo-Hookean membrane with
$X_{2}^{(0)}=0$). The solid line corresponds to a neo-Hookean membrane with 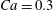 $Ca=0.3$ (figure 12). The dashed lines correspond to a Skalak membrane (
$Ca=0.3$ (figure 12). The dashed lines correspond to a Skalak membrane (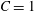 $C=1$); ○
$C=1$); ○ 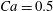 $Ca=0.5$, ▫
$Ca=0.5$, ▫  $Ca=1.0$. Open symbols: leapfrog motion; filled symbols: minuet motion.
$Ca=1.0$. Open symbols: leapfrog motion; filled symbols: minuet motion.
5.2 Doublet duration

Figure 14. Effect of  $Ca$,
$Ca$, 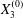 $X_{3}^{(0)}$ and constitutive law on the times
$X_{3}^{(0)}$ and constitutive law on the times  $\dot{\unicode[STIX]{x1D6FE}}t_{1}$ and
$\dot{\unicode[STIX]{x1D6FE}}t_{1}$ and 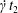 $\dot{\unicode[STIX]{x1D6FE}}t_{2}$ of first and second crossings (
$\dot{\unicode[STIX]{x1D6FE}}t_{2}$ of first and second crossings (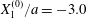 $X_{1}^{(0)}/a=-3.0$ and
$X_{1}^{(0)}/a=-3.0$ and 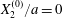 $X_{2}^{(0)}/a=0$).
$X_{2}^{(0)}/a=0$).

Figure 15. Projection of  $G_{2}$ trajectories for
$G_{2}$ trajectories for 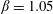 $\unicode[STIX]{x1D6FD}=1.05$,
$\unicode[STIX]{x1D6FD}=1.05$, 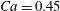 $Ca=0.45$ and different initial positions. Capsule
$Ca=0.45$ and different initial positions. Capsule  $C_{2}$ starts from
$C_{2}$ starts from 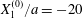 $X_{1}^{(0)}/a=-20$,
$X_{1}^{(0)}/a=-20$, 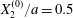 $X_{2}^{(0)}/a=0.5$ and different
$X_{2}^{(0)}/a=0.5$ and different 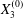 $X_{3}^{(0)}$. The comparison between the results of Lac & Barthès-Biesel (symbols) and the present results (lines) shows very good agreement.
$X_{3}^{(0)}$. The comparison between the results of Lac & Barthès-Biesel (symbols) and the present results (lines) shows very good agreement.
The minuet motion, when it occurs, is very slow, as shown in figure 14 for 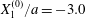 $X_{1}^{(0)}/a=-3.0$ and
$X_{1}^{(0)}/a=-3.0$ and  $X_{2}^{(0)}/a=0$. The time
$X_{2}^{(0)}/a=0$. The time  $\dot{\unicode[STIX]{x1D6FE}}t_{1}$, at which the first crossing occurs, increases with the separation
$\dot{\unicode[STIX]{x1D6FE}}t_{1}$, at which the first crossing occurs, increases with the separation 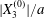 $|X_{3}^{(0)}|/a$, but does not depend on
$|X_{3}^{(0)}|/a$, but does not depend on  $Ca$, the membrane law or the type of motion (leapfrog or minuet). The fact that
$Ca$, the membrane law or the type of motion (leapfrog or minuet). The fact that 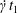 $\dot{\unicode[STIX]{x1D6FE}}t_{1}$ increases with
$\dot{\unicode[STIX]{x1D6FE}}t_{1}$ increases with 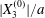 $|X_{3}^{(0)}|/a$ is due to the fact that the relative velocity of
$|X_{3}^{(0)}|/a$ is due to the fact that the relative velocity of 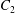 $C_{2}$, which is initially zero, builds up from a flow perturbation (due to
$C_{2}$, which is initially zero, builds up from a flow perturbation (due to 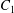 $C_{1}$), the intensity of which decreases with the square of the distance between the two capsules. The time
$C_{1}$), the intensity of which decreases with the square of the distance between the two capsules. The time 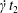 $\dot{\unicode[STIX]{x1D6FE}}t_{2}$ of the second crossing is quite large and increases significantly with capsule deformability and distance.
$\dot{\unicode[STIX]{x1D6FE}}t_{2}$ of the second crossing is quite large and increases significantly with capsule deformability and distance.
This means that the two capsules remain close to each other for a long time, while drifting slowly. When 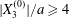 $|X_{3}^{(0)}|/a\geqslant 4$,
$|X_{3}^{(0)}|/a\geqslant 4$,  $\dot{\unicode[STIX]{x1D6FE}}t_{2}$ becomes too large to be reliably computed (the values of
$\dot{\unicode[STIX]{x1D6FE}}t_{2}$ becomes too large to be reliably computed (the values of  $\dot{\unicode[STIX]{x1D6FE}}t_{2}$ for
$\dot{\unicode[STIX]{x1D6FE}}t_{2}$ for 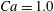 $Ca=1.0$ and a SK membrane are very high, and are included here to illustrate the phenomenon).
$Ca=1.0$ and a SK membrane are very high, and are included here to illustrate the phenomenon).
6 Discussion and conclusion
The situation that we have studied pertains to a semi-dilute suspension of capsules that is suddenly put in motion by a simple shear flow. The novel aspect of our work is that we consider a pair of nearby capsules with their centres in (or near) the plane normal to the velocity gradient (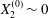 $X_{2}^{(0)}\sim 0$). This capsule configuration had never been studied before, because it entails long computations. Indeed, the only results on capsule interaction off the shear plane had been obtained for capsules with a significant relative velocity, which prevented minuet from occurring and which led to weak capsule interactions and small trajectory displacement.
$X_{2}^{(0)}\sim 0$). This capsule configuration had never been studied before, because it entails long computations. Indeed, the only results on capsule interaction off the shear plane had been obtained for capsules with a significant relative velocity, which prevented minuet from occurring and which led to weak capsule interactions and small trajectory displacement.
When 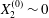 $X_{2}^{(0)}\sim 0$, the important results are:
$X_{2}^{(0)}\sim 0$, the important results are:
(i) The capsule pair can remain stable for a long time, while dancing a minuet.
(ii) When they separate, the capsules can reverse direction.
(iii) When one or more oscillations occur, the irreversible trajectory shift is large.
(iv) This minuet dance progressively leads the capsules to closely interact and deform significantly.
(v) The less deformable the capsule, the more prone it is to do a minuet.
(vi) The zone where a minuet can occur has been identified.
During the close interaction, the film thickness between the two capsules is of the order of 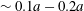 ${\sim}0.1a-0.2a$. For small capsules, this may lead to physico-chemical interaction.
${\sim}0.1a-0.2a$. For small capsules, this may lead to physico-chemical interaction.
In order to make the problem consistent, we considered as an initial condition a suspension of spherical capsules at rest, and suddenly started the flow. When the capsules are pre-deformed to the profile that they would have if they were alone in the flow, we have verified that they take the same motion (leapfrog or minuet) as if they were initially spherical: the only difference is that, for pre-deformed capsules, the first close interaction happens 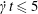 $\dot{\unicode[STIX]{x1D6FE}}t\leqslant 5$ earlier than for spherical capsules. It follows that the minuet interaction is not restricted to the transient start of the flow of a suspension. For example, from figure 6, we note that, at the end of the interaction, when
$\dot{\unicode[STIX]{x1D6FE}}t\leqslant 5$ earlier than for spherical capsules. It follows that the minuet interaction is not restricted to the transient start of the flow of a suspension. For example, from figure 6, we note that, at the end of the interaction, when 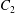 $C_{2}$ is located at
$C_{2}$ is located at 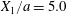 $X_{1}/a=5.0$,
$X_{1}/a=5.0$, 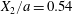 $X_{2}/a=0.54$,
$X_{2}/a=0.54$, 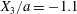 $X_{3}/a=-1.1$, it has almost recovered its equilibrium shape. Suppose that
$X_{3}/a=-1.1$, it has almost recovered its equilibrium shape. Suppose that 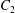 $C_{2}$ then meets a new capsule
$C_{2}$ then meets a new capsule  $C_{3}$, located in the vicinity of
$C_{3}$, located in the vicinity of 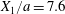 $X_{1}/a=7.6$,
$X_{1}/a=7.6$, 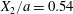 $X_{2}/a=0.54$,
$X_{2}/a=0.54$, 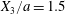 $X_{3}/a=1.5$. Being in the same relative configuration as
$X_{3}/a=1.5$. Being in the same relative configuration as 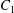 $C_{1}$ and
$C_{1}$ and 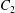 $C_{2}$ were at time
$C_{2}$ were at time  $t=0$, capsules
$t=0$, capsules  $C_{2}$ and
$C_{2}$ and 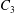 $C_{3}$ will do a minuet. We can thus expect minuet motions in semi-dilute suspensions.
$C_{3}$ will do a minuet. We can thus expect minuet motions in semi-dilute suspensions.
In conclusion, we have shown a novel and unexpected effect in the pair interaction of two capsules, that depends on the relative position of the two particles. It would be interesting to check experimentally the existence of long lasting capsule doublets that do a minuet motion.
Acknowledgements
This work was supported by the European Research Council (ERC) Consolidator grant (MultiphysMicroCaps, no. 772191), by the National Natural Science Foundation of China (no. 11402084) and by the China Scholarship Council (Visiting Scholar Scholarship of X.-Q.H.).
Declaration of interests
The authors report no conflict of interest.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2020.181.
Appendix
The results of the BI–FE model (1280 elements) are first compared to those obtained by Lac et al. (Reference Lac, Morel and Barthès-Biesel2007) and Lac & Barthès-Biesel (Reference Lac and Barthès-Biesel2008) for two pre-inflated capsules with a NH membrane and radius 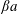 $\unicode[STIX]{x1D6FD}a$, where
$\unicode[STIX]{x1D6FD}a$, where 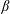 $\unicode[STIX]{x1D6FD}$ is the inflation ratio. The pre-stress is created by means of an internal pressure
$\unicode[STIX]{x1D6FD}$ is the inflation ratio. The pre-stress is created by means of an internal pressure  $p_{0}$, which leads to an isotropic elastic tension
$p_{0}$, which leads to an isotropic elastic tension 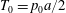 $T_{0}=p_{0}a/2$, given by Laplace’s law. For a neo-Hookean membrane,
$T_{0}=p_{0}a/2$, given by Laplace’s law. For a neo-Hookean membrane,  $T_{0}=6G_{s}(\unicode[STIX]{x1D6FD}-1)$ in the limit of small inflation. The trajectories of
$T_{0}=6G_{s}(\unicode[STIX]{x1D6FD}-1)$ in the limit of small inflation. The trajectories of 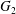 $G_{2}$ obtained with the two methods show very good agreement, as illustrated in figure 15 for
$G_{2}$ obtained with the two methods show very good agreement, as illustrated in figure 15 for 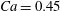 $Ca=0.45$.
$Ca=0.45$.

Figure 16. Effect of numerical parameters on the 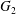 $G_{2}$ trajectory, projected on the
$G_{2}$ trajectory, projected on the 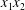 $x_{1}x_{2}$- and
$x_{1}x_{2}$- and 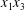 $x_{1}x_{3}$-planes for SK membranes, for
$x_{1}x_{3}$-planes for SK membranes, for  $Ca=0.5$,
$Ca=0.5$, 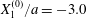 $X_{1}^{(0)}/a=-3.0$,
$X_{1}^{(0)}/a=-3.0$,  $X_{2}^{(0)}/a=0$,
$X_{2}^{(0)}/a=0$,  $X_{3}^{(0)}/a=-2.4$. (a,b) Effect of time step for 1280 elements. (c,d) Effect of mesh refinement for
$X_{3}^{(0)}/a=-2.4$. (a,b) Effect of time step for 1280 elements. (c,d) Effect of mesh refinement for 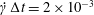 $\dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x0394}t=2\times 10^{-3}$.
$\dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x0394}t=2\times 10^{-3}$.
As the minuet motion is a novel phenomenon, which occurs over fairly long times, it is of importance to verify that the trajectories do not suffer from error accumulation over time. The test case consists of two capsules enclosed by a SK membrane ( $C=1$) with
$C=1$) with 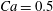 $Ca=0.5$,
$Ca=0.5$, 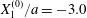 $X_{1}^{(0)}/a=-3.0$,
$X_{1}^{(0)}/a=-3.0$, 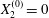 $X_{2}^{(0)}=0$ and
$X_{2}^{(0)}=0$ and 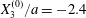 $X_{3}^{(0)}/a=-2.4$. As shown in figure 13, those capsules undergo a minuet with one reversal. The choice of a SK law rather than a NH one enables us to use larger values of
$X_{3}^{(0)}/a=-2.4$. As shown in figure 13, those capsules undergo a minuet with one reversal. The choice of a SK law rather than a NH one enables us to use larger values of  $Ca$, and thus larger time steps for similar trajectories. As shown in figure 16(a) for 1280 elements on the capsule surfaces, decreasing the time step
$Ca$, and thus larger time steps for similar trajectories. As shown in figure 16(a) for 1280 elements on the capsule surfaces, decreasing the time step 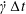 $\dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x0394}t$ from
$\dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x0394}t$ from 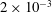 $2\times 10^{-3}$ to
$2\times 10^{-3}$ to 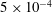 $5\times 10^{-4}$ has no effect on the trajectory. Conversely, we keep the same time step
$5\times 10^{-4}$ has no effect on the trajectory. Conversely, we keep the same time step  $\dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x0394}t=2\times 10^{-3}$ and compare the trajectories obtained with two spatial meshes with 1280 or 5120 elements, corresponding to mesh sizes
$\dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x0394}t=2\times 10^{-3}$ and compare the trajectories obtained with two spatial meshes with 1280 or 5120 elements, corresponding to mesh sizes 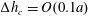 $\unicode[STIX]{x0394}h_{c}=O(0.1a)$ and
$\unicode[STIX]{x0394}h_{c}=O(0.1a)$ and  $O(0.05a)$, respectively. As shown in figure 16(b), the trajectories differ by at most one (fine) mesh size at the interaction point. We conclude that the trajectories that are presented in this study using 1280 elements and
$O(0.05a)$, respectively. As shown in figure 16(b), the trajectories differ by at most one (fine) mesh size at the interaction point. We conclude that the trajectories that are presented in this study using 1280 elements and 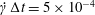 $\dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x0394}t=5\times 10^{-4}$, are reliable and that the final trajectory shifts
$\dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x0394}t=5\times 10^{-4}$, are reliable and that the final trajectory shifts 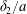 $\unicode[STIX]{x1D6FF}_{2}/a$ and
$\unicode[STIX]{x1D6FF}_{2}/a$ and  $\unicode[STIX]{x1D6FF}_{3}/a$ have an error of the order of
$\unicode[STIX]{x1D6FF}_{3}/a$ have an error of the order of  $0.05a$.
$0.05a$.