Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T07:02:40.614Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimum power consumption for drag reduction on a circular cylinder by tangential surface motion

Published online by Cambridge University Press:  09 January 2013

Ratnesh K. Shukla  and
Jaywant H. Arakeri
Ratnesh K. Shukla*
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore 560012, India
Jaywant H. Arakeri
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore 560012, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the effect of a prescribed tangential velocity on the drag force on a circular cylinder in a spanwise uniform cross flow. Using a combination of theoretical and numerical techniques we make an attempt at determining the optimal tangential velocity profiles which will reduce the drag force acting on the cylindrical body while minimizing the net power consumption characterized through a non-dimensional power loss coefficient (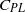${C}_{\mathit{PL}} $). A striking conclusion of our analysis is that the tangential velocity associated with the potential flow, which completely suppresses the drag force, is not optimal for both small and large, but finite Reynolds number. When inertial effects are negligible (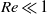$\mathit{Re}\ll 1$), theoretical analysis based on two-dimensional Oseen equations gives us the optimal tangential velocity profile which leads to energetically efficient drag reduction. Furthermore, in the limit of zero Reynolds number (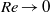$\mathit{Re}\ensuremath{\rightarrow} 0$), minimum power loss is achieved for a tangential velocity profile corresponding to a shear-free perfect slip boundary. At finite 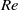$\mathit{Re}$, results from numerical simulations indicate that perfect slip is not optimum and a further reduction in drag can be achieved for reduced power consumption. A gradual increase in the strength of a tangential velocity which involves only the first reflectionally symmetric mode leads to a monotonic reduction in drag and eventual thrust production. Simulations reveal the existence of an optimal strength for which the power consumption attains a minima. At a Reynolds number of 100, minimum value of the power loss coefficient (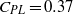${C}_{\mathit{PL}} = 0. 37$) is obtained when the maximum in tangential surface velocity is about one and a half times the free stream uniform velocity corresponding to a percentage drag reduction of approximately 77 %; 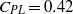${C}_{\mathit{PL}} = 0. 42$ and 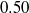$0. 50$ for perfect slip and potential flow cases, respectively. Our results suggest that potential flow tangential velocity enables energetically efficient propulsion at all Reynolds numbers but optimal drag reduction only for 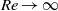$\mathit{Re}\ensuremath{\rightarrow} \infty $. The two-dimensional strategy of reducing drag while minimizing net power consumption is shown to be effective in three dimensions via numerical simulation of flow past an infinite circular cylinder at a Reynolds number of 300. Finally a strategy of reducing drag, suitable for practical implementation and amenable to experimental testing, through piecewise constant tangential velocities distributed along the cylinder periphery is proposed and analysed.

JFM classification

Flow Control: Drag reduction Flow Control: Flow Control Biological Fluid Dynamics: Propulsion
Type
Papers
Information
Journal of Fluid Mechanics , Volume 715 , 25 January 2013 , pp. 597 - 641
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. 1968 Handbook of Mathematical Functions. Dover.Google Scholar
Arakeri, J. H. & Shukla, R. K. 2012 A unified view of energetic efficiency in active drag reduction, thrust generation and self-propulsion through a loss coefficient with some applications. J. Fluid Struct. (submitted).CrossRefGoogle Scholar
Auteri, F., Parolini, N. & Quartapelle, L. 2002 Numerical investigation on the stability of singular driven cavity flow. J. Comput. Phys. 183, 1–25.CrossRefGoogle Scholar
Barkley, D. & Henderson, R. D. 1996 Three-dimensional floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Beaudoin, J.-F., Cadot, O., Aider, J.-L. & Wesfreid, J.-E. 2006 Drag reduction of a bluff body using adaptive control methods. Phys. Fluids 18, 085107.Google Scholar
Bechert, D. W., Hage, W. & Brusek, M. 1996 Drag reduction with the slip wall. AIAA J. 34 (5), 1072–1074.CrossRefGoogle Scholar
Bergmann, M. & Cordier, L. 2008 Optimal control of the cylinder wake in the laminar regime by trust-region methods and POD reduced-order models. J. Comput. Phys. 227, 7813–7840.Google Scholar
Bergmann, M., Cordier, L. & Brancher, J.-P. 2005 Optimal rotary control of the cylinder wake using proper orthogonal decomposition reduced-order model. Phys. Fluids 17, 097101.CrossRefGoogle Scholar
Bergmann, M., Cordier, L. & Brancher, J.-P. 2006 On the generation of a reverse von Karman street for the controlled cylinder wake in the laminar regime. Phys. Fluids 18, 028101.Google Scholar
Blackburn, H. M., Elston, J. R. & Sheridan, J. 1999 Bluff-body propulsion produced by combined rotary and translational oscillation. Phys. Fluids 11, 4–6.Google Scholar
Blanco, A. & Magnaudet, J. 1995 The structure of the axisymmetric high-Reynolds number flow around an ellipsoidal bubble of fixed shape. Phys. Fluids 7, 1265–1274.Google Scholar
Botella, O. & Peyret, R. 1998 Benchmark spectral results on the lid-driven cavity flow. Comput. Fluids 27, 421–433.CrossRefGoogle Scholar
Chan, A. S., Dewey, P. A., Jameson, A., Liang, C. & Smits, A. J. 2011 Vortex suppression and drag reduction in the wake of counter-rotating cylinders. J. Fluid Mech. 679, 343–382.Google Scholar
Choi, B. & Choi, H. 2000 Drag reduction with a sliding wall in flow over a circular cylinder. AIAA J. 38 (4), 715–717.Google Scholar
Choi, S., Choi, H. & Kang, S. 2002 Characteristics of flow over a rotationally oscillating cylinder at low Reynolds number. Phys. Fluids 14, 2767–2777.Google Scholar
Choi, H., Jeon, W.-P. & Kim, J. 2008 Control of flow over a bluff body. Annu. Rev. Fluid Mech. 40, 113–139.CrossRefGoogle Scholar
Dennis, S. C. R. & Chang, G.-Z. 1970 Numerical solutions for steady flow past a circular cylinder at Reynolds numbers up to 100. J. Fluid Mech. 42, 471–489.Google Scholar
Dong, S., Triantafyllou, G. S. & Karniadakis, G. E. 2008 Elimination of vortex streets in bluff-body flows. Phys. Rev. Lett. 100, 204501.Google Scholar
Happel, J. & Brenner, H. 1965 Low Reynolds Number Hydrodynamics. Prentice-Hall.Google Scholar
He, J.-W., Glowinski, R., Metcalfe, R., Nordlander, A. & Periaux, J. 2000 Active control and drag optimization for flow past a circular cylinder. I. Oscillatory cylinder rotation. J. Comput. Phys. 163, 83–117.Google Scholar
Henderson, R. D. 1994 Unstructured spectral element methods: parallel algorithms and simulations. PhD thesis, Princeton University.Google Scholar
Homescu, C., Navon, I. M. & Li, Z. 2002 Suppression of vortex shedding for flow around a circular cylinder using optimal control. Intl J. Numer. Meth. Fluids 38, 43–69.Google Scholar
Hugues, S. & Randriamampianina, A. 1998 An improved projection scheme applied to pseudospectral methods for the incompressible Navier–Stokes equations. Intl J Numer. Meth. Fluids 28, 501–521.Google Scholar
Jeon, S. & Choi, H. 2005 Suboptimal feedback control for drag reduction in flow over a sphere. Bull. Am. Phys. Soc.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Joseph, D. D., Funada, T. & Wang, J. 2007 Potential Flows of Viscous and Viscoelastic Fluids. Cambridge University Press.CrossRefGoogle Scholar
Karniadakis, G. E. & Choi, K.-S. 2003 Mechanisms on transverse motions in turbulent wall flows. Annu. Rev. Fluid Mech. 35, 45–62.Google Scholar
Kim, J. & Choi, H. 2005 Distributed forcing of flow over a circular cylinder. Phys. Fluids 17, 033103.Google Scholar
Kleiser, L. & Schumann, U. 1980 Treatment of incompressibility and boundary conditions in 3-D numerical spectral simulations of plane channel flows. Proceedings, 3rd GAMM Conference on Numerical Methods in Fluid Mechanics, pp. 165–169.Google Scholar
Koplik, J. & Banavar, J. R. 1995 Corner flow in the sliding plate problem. Phys. Fluids 7, 3118–3125.Google Scholar
Kumar, S., Gonzalez, B. & Probst, O. 2011 Flow past two rotating cylinders. Phys. Fluids 23, 014102.Google Scholar
Lamb, H. 1932 Hydrodynamics. Cambridge University Press.Google Scholar
Lauga, E. & Powers, T. R. 2009 The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 72, 096601.Google Scholar
Leal, L. G. 1989 Vorticity transport and wake structure for bluff bodies at finite Reynolds number. Phys. Fluids 1, 124–131.CrossRefGoogle Scholar
Legendre, D., Lauga, E. & Magnaudet, J. 2009 Influence of slip on the dynamics of two-dimensional wakes. J. Fluid Mech. 633, 437–447.Google Scholar
Leschziner, M. A., Choi, H. & Choi, K.-S. 2011 Flow-control approaches to drag reduction in aerodynamics: progress and prospects. Phil. Trans. R. Soc. A 369, 1349–1351.CrossRefGoogle ScholarPubMed
Leshansky, A. M., Kenneth, O., Gat, O. & Avron, J. E. 2007 A frictionless microswimmer. New J. Phys. Fluids 9, 145.Google Scholar
Lighthill, M. J. 1952 On the squirming motion of nearly spherical deformable bodies through liquids at very small Reynolds numbers. Commun. Pure Appl. Maths 5, 109–118.Google Scholar
Liu, C., Zheng, X. & Sung, C. H. 1998 Preconditioned multigrid methods for unsteady incompressible flows. J. Comput. Phys. 139, 35–57.Google Scholar
Magnaudet, J. & Eames, I. 2000 The motion of high-Reynolds-number bubbles in inhomogeneous flows. Annu. Rev. Fluid Mech. 32, 659–708.Google Scholar
Milano, M. & Koumoutsakos, P. 2002 A clustering genetic algorithm for cylinder drag optimization. J. Comput. Phys. 175, 79–107.Google Scholar
Mittal, R. & Balachandar, S. 1996 Direct numerical simulation of flow past elliptic cylinders. J. Comput. Phys. 124, 351–367.Google Scholar
Mittal, S. & Kumar, B. 2003 Flow past a rotating cylinder. J. Fluid Mech. 476, 303–334.CrossRefGoogle Scholar
Modi, V. J. 1997 Moving surface boundary-layer control: a review. J. Fluid. Struct. 11, 627–663.Google Scholar
Moore, D. W. 1963 The boundary layer on a spherical gas bubble. J. Fluid Mech. 16, 161–176.Google Scholar
Muralidhar, P., Ferrer, N., Daniello, R. & Rothstein, J. P. 2011 Influence of slip on the flow past superhydrophobic circular cylinders. J. Fluid Mech. 680, 459–476.Google Scholar
Nazarinia, M., Jacono, D. L., Thompson, M. C. & Sheridan, J. 2009 The three-dimensional wake of a cylinder undergoing a combination of translational and rotational oscillation in a quiescent fluid. Phys. Fluids 21, 064101.Google Scholar
Nie, X., Robbins, M. O. & Chen, S. 2006 Resolving singular forces in cavity flow: multiscale modelling from atomic to millimetre scales. Phys. Rev. Lett. 96, 134501.Google Scholar
Peyret, R. 2001 Spectral Methods for Incompressible Viscous Flow. Springer.Google Scholar
Poncet, P. 2004 Topological aspects of three-dimensional wakes behind rotary oscillating cylinders. J. Fluid Mech. 517, 27–53.Google Scholar
Poncet, P., Hildebrand, R., Cottet, G.-H. & Koumoutsakos, P. 2008 Spatially distributed control for optimal drag reduction of the flow past a circular cylinder. J. Fluid Mech. 599, 111–120.Google Scholar
Poncet, P. & Koumoutsakos, P. 2005 Optimization of vortex shedding in 3-D wakes using belt actuators. Intl J. Offshore Polar Engng 15, 1–7.Google Scholar
Prandtl, L. & Tietjens, O. G. 1957 Applied Hydro- and Aerodynamics. Dover.Google Scholar
Protas, B. & Styczek, A. 2002 Optimal rotary control of the cylinder wake in the laminar regime. Phys. Fluids 14, 2073–2087.CrossRefGoogle Scholar
Purcell, E. M. 1977 Life at low Reynolds number. Am. J. Phys. 45, 3–11.Google Scholar
Qian, T. & Wang, X.-P. 2005 Driven cavity flow: from molecular dynamics to continuum hydrodynamics. SIAM Multiscale Model. Simul. 3, 749–763.Google Scholar
Rothstein, J. P. 2010 Slip on superhydrophobic surfaces. Annu. Rev. Fluid Mech. 42, 89–109.Google Scholar
Schlichting, H. 1960 Boundary Layer Theory. McGraw-Hill.Google Scholar
Shiels, D. & Leonard, A. 2001 Investigation of a drag reduction on a circular cylinder in rotary oscillation. J. Fluid Mech. 431, 297–322.CrossRefGoogle Scholar
Shukla, R. K., Tatineni, M. & Zhong, X. 2007 Very high-order compact finite difference schemes on non-uniform grids for incompressible Navier–Stokes equations. J. Comput. Phys. 224, 1064–1094.Google Scholar
Shukla, R. K. & Zhong, X. 2005 Derivation of high-order compact finite difference schemes for non-uniform grid using polynomial interpolation. J. Comput. Phys. 204, 404–429.Google Scholar
Sneddon, I. N. 1966 Mixed boundary value problems in potential theory. John Wiley & Sons.Google Scholar
Spalart, P. R. & McLean, J. D. 2011 Drag reduction: enticing turbulence, and then an industry. Phil. Trans. R. Soc. A 369, 1556–1569.Google Scholar
Stone, H. A. & Samuel, A. D. T. 1996 Propulsion of microorganisms by surface distortions. Phys. Rev. Lett. 77, 4102–4104.Google Scholar
Taylor, G. I. 1952 The action of waving cylindrical tails in propelling microscopic organisms. Proc. R. Soc. A 211, 225–239.Google Scholar
Thiria, B., Goujon-Durand, S. & Wesfreid, J. E. 2006 The wake of a cylinder performing rotary oscillations. J. Fluid Mech. 560, 123–147.Google Scholar
Tokumaru, P. T. & Dimotakis, P. E. 1991 Rotary oscillation control of a cylinder wake. J. Fluid Mech. 224, 77–90.CrossRefGoogle Scholar
Tomotika, S. & Aoi, T. 1950 The steady flow of viscous fluid past a sphere and circular cylinder at small Reynolds numbers. Q. J. Mech. Appl. Maths 3, 140–161.Google Scholar
Veysey, J. & Goldenfeld, N. 2007 Simple viscous flows: from boundary layers to the renormalization group. Rev. Mod. Phys. 79, 883–927.Google Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.Google Scholar
Yoon, H. S., Kim, J. H., Chun, H. H. & Choi, H. J. 2007 Laminar flow past two rotating circular cylinders in a side-by-side arrangement. Phys. Fluids 19, 128103.Google Scholar
You, D. & Moin, P. 2007 Effects of hydrophobic surfaces on the drag and lift of a circular cylinder. Phys. Fluids 19, 081701.CrossRefGoogle Scholar