Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T05:43:53.993Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimal multi-scale dynamics of near-wall turbulence

Published online by Cambridge University Press:  26 February 2021

Patrick Doohan Open the ORCID record for Patrick Doohan [Opens in a new window] ,
Ashley P. Willis Open the ORCID record for Ashley P. Willis [Opens in a new window]  and
Yongyun Hwang Open the ORCID record for Yongyun Hwang [Opens in a new window]
Patrick Doohan
Affiliation:
Department of Aeronautics, Imperial College London, LondonSW7 2AZ, UK
Ashley P. Willis
Affiliation:
School of Mathematics and Statistics, University of Sheffield, SheffieldS3 7RH, UK
Yongyun Hwang*
Affiliation:
Department of Aeronautics, Imperial College London, LondonSW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

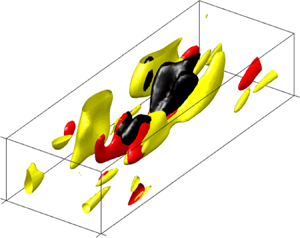
Recent numerical experiments have shown that the temporal dynamics of isolated energy-containing eddies in the hierarchy of wall-bounded turbulence are governed by the self-sustaining process (SSP). However, high-Reynolds-number turbulence is a multi-scale phenomenon and exhibits interaction between the structures of different scales, but the dynamics of such multi-scale flows are poorly understood. In this study, the temporal dynamics of near-wall turbulent flow with two integral length scales of motion are investigated using a shear stress-driven flow model (Doohan et al., J. Fluid Mech., vol. 874, 2019, pp. 606–638), with a focus on identifying scale interaction processes through the governing equations and relating these to the SSPs at each scale. It is observed that the dynamics of the energy cascade from large to small scales is entirely determined by the large-scale SSP and the timing of the corresponding inter-scale turbulent transport coincides with the large-scale streak breakdown stage. Furthermore, the characteristic time scales of the resulting small-scale dissipation match those of the large-scale SSP, indicative of non-equilibrium turbulent dissipation dynamics. A new scale interaction process is identified, namely that the transfer of wall-normal energy from large to small scales drives small-scale turbulent production via the Orr mechanism. While the main outcome of this driving process appears to be the transient amplification of localised small-scale velocity structures and their subsequent dissipation, it also has an energising effect on the small-scale SSP. Finally, the feeding of energy from small to large scales is impelled by the small-scale SSP and coincides with the small-scale streak instability stage. The streamwise feeding process seems to be related to the subharmonic sinuous streak instability mode in particular and leads to the formation of the wall-reaching part of high-speed large-scale streaks.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulence theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 913 , 25 April 2021 , A8
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Afzal, N. 1984 Mesolayer theory for turbulent flows. AIAA J. 22 (3), 437–439.CrossRefGoogle Scholar
Agostini, L. & Leschziner, M. 2016 Predicting the response of small-scale near-wall turbulence to large-scale outer motions. Phys. Fluids 28 (1), 015107.CrossRefGoogle Scholar
del Alamo, J.C. & Jimenez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.CrossRefGoogle Scholar
del Álamo, J.C., Jimenez, J., Zandonade, P. & Moser, R.D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.CrossRefGoogle Scholar
Alizard, F. 2015 Linear stability of optimal streaks in the log-layer of turbulent channel flows. Phys. Fluids 27 (10), 105103.CrossRefGoogle Scholar
Baars, W.J. & Marusic, I. 2020 a Data-driven decomposition of the streamwise turbulence kinetic energy in boundary layers. Part 1. Energy spectra. J. Fluid Mech. 882, A25.CrossRefGoogle Scholar
Baars, W.J. & Marusic, I. 2020 b Data-driven decomposition of the streamwise turbulence kinetic energy in boundary layers. Part 2. Integrated energy and ${A}_1$. J. Fluid Mech. 882, A26.CrossRefGoogle Scholar
Berkooz, G., Holmes, P. & Lumley, J.L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25 (1), 539–575.CrossRefGoogle Scholar
Bewley, T.R. 2014 Numerical Renaissance: Simulation, Optimization, & Control. Renaissance Press.Google Scholar
Butler, K.M. & Farrell, B.F. 1993 Optimal perturbations and streak spacing in wall-bounded turbulent shear flow. Phys. Fluids A: Fluid Dyn. 5 (3), 774–777.CrossRefGoogle Scholar
Cafiero, G. & Vassilicos, J.C. 2019 Non-equilibrium turbulence scalings and self-similarity in turbulent planar jets. Proc. R. Soc. A 475 (2225), 20190038.CrossRefGoogle ScholarPubMed
Cassinelli, A., de Giovanetti, M. & Hwang, Y. 2017 Streak instability in near-wall turbulence revisited. J. Turbul. 18 (5), 443–464.CrossRefGoogle Scholar
Cheng, C., Li, W., Lozano-Durán, A. & Liu, H. 2019 Identity of attached eddies in turbulent channel flows with bidimensional empirical mode decomposition. J. Fluid Mech. 870, 1037–1071.CrossRefGoogle ScholarPubMed
Cho, M., Hwang, Y. & Choi, H. 2018 Scale interactions and spectral energy transfer in turbulent channel flow. J. Fluid Mech. 854, 474–504.CrossRefGoogle Scholar
Cimarelli, A., De Angelis, E., Jimenez, J. & Casciola, C.M. 2016 Cascades and wall-normal fluxes in turbulent channel flows. J. Fluid Mech. 796, 417–436.CrossRefGoogle Scholar
Doohan, P., Willis, A.P. & Hwang, Y. 2019 Shear stress-driven flow: the state space of near-wall turbulence as ${R}e_\tau \rightarrow \infty$. J. Fluid Mech. 874, 606–638.CrossRefGoogle Scholar
Duvvuri, S. & McKeon, B.J. 2015 Triadic scale interactions in a turbulent boundary layer. J. Fluid Mech. 767, R4.CrossRefGoogle Scholar
Eckhardt, B. & Zammert, S. 2018 Small scale exact coherent structures at large Reynolds numbers in plane Couette flow. Nonlinearity 31 (2), R66.CrossRefGoogle Scholar
Encinar, M.P. & Jiménez, J. 2020 Momentum transfer by linearised eddies in turbulent channel flows (submitted).CrossRefGoogle Scholar
de Giovanetti, M., Hwang, Y. & Choi, H. 2016 Skin-friction generation by attached eddies in turbulent channel flow. J. Fluid Mech. 808, 511–538.CrossRefGoogle Scholar
de Giovanetti, M., Sung, H.J. & Hwang, Y. 2017 Streak instability in turbulent channel flow: the seeding mechanism of large-scale motions. J. Fluid Mech. 832, 483–513.CrossRefGoogle Scholar
Goto, S. & Vassilicos, J.C. 2015 Energy dissipation and flux laws for unsteady turbulence. Phys. Lett. A 379 (16–17), 1144–1148.CrossRefGoogle Scholar
Hamilton, J.M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.CrossRefGoogle Scholar
Hellström, L., Marusic, I. & Smits, A.J. 2016 Self-similarity of the large-scale motions in turbulent pipe flow. J. Fluid Mech. 792, R1.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. A: Math. Phys. Engng Sci. 365 (1852), 647–664.CrossRefGoogle ScholarPubMed
Hwang, Y. 2013 Near-wall turbulent fluctuations in the absence of wide outer motions. J. Fluid Mech. 723, 264–288.CrossRefGoogle Scholar
Hwang, Y. 2015 Statistical structure of self-sustaining attached eddies in turbulent channel flow. J. Fluid Mech. 767, 254–289.CrossRefGoogle Scholar
Hwang, Y. 2016 Mesolayer of attached eddies in turbulent channel flow. Phys. Rev. Fluids 1 (6), 064401.CrossRefGoogle Scholar
Hwang, Y. & Bengana, Y. 2016 Self-sustaining process of minimal attached eddies in turbulent channel flow. J. Fluid Mech. 795, 708–738.CrossRefGoogle Scholar
Hwang, Y. & Cossu, C. 2010 a Linear non-normal energy amplification of harmonic and stochastic forcing in the turbulent channel flow. J. Fluid Mech. 664, 51–73.CrossRefGoogle Scholar
Hwang, Y. & Cossu, C. 2010 b Self-sustained process at large scales in turbulent channel flow. Phys. Rev. Lett. 105 (4), 044505.CrossRefGoogle ScholarPubMed
Hwang, Y. & Cossu, C. 2011 Self-sustained processes in the logarithmic layer of turbulent channel flows. Phys. Fluids 23 (6), 061702.CrossRefGoogle Scholar
Hwang, J. & Sung, H.J. 2018 Wall-attached structures of velocity fluctuations in a turbulent boundary layer. J. Fluid Mech. 856, 958–983.CrossRefGoogle Scholar
Jiménez, J. 2013 How linear is wall-bounded turbulence? Phys. Fluids 25 (11), 110814.CrossRefGoogle Scholar
Jiménez, J. 2015 Direct detection of linearized bursts in turbulence. Phys. Fluids 27 (6), 065102.CrossRefGoogle Scholar
Jimenez, J. & Hoyas, S. 2008 Turbulent fluctuations above the buffer layer of wall-bounded flows. J. Fluid Mech. 611, 215–236.CrossRefGoogle Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.CrossRefGoogle Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.CrossRefGoogle Scholar
von Kármán, T. 1930 Mechanische änlichkeit und turbulenz. In Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse, pp. 58–76 (English translation NACA TM 611).Google Scholar
Kawata, T. & Alfredsson, P.H. 2018 Inverse interscale transport of the Reynolds shear stress in plane Couette turbulence. Phys. Rev. Lett. 120 (24), 244501.CrossRefGoogle ScholarPubMed
Kawata, T. & Alfredsson, P.H. 2019 Scale interactions in turbulent rotating planar Couette flow: insight through the Reynolds stress transport. J. Fluid Mech. 879, 255–295.CrossRefGoogle Scholar
Kim, J. 1989 On the structure of pressure fluctuations in simulated turbulent channel flow. J. Fluid Mech. 205, 421–451.CrossRefGoogle Scholar
Kim, J. & Moin, P. 1985 Application of a fractional-step method to incompressible Navier–Stokes equations. J. Comput. Phys. 59 (2), 308–323.CrossRefGoogle Scholar
Klewicki, J.C. 2013 Self-similar mean dynamics in turbulent wall flows. J. Fluid Mech. 718, 596–621.CrossRefGoogle Scholar
Kolmogorov, A.N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. C. R. Acad. Sci. URSS 30, 301–305.Google Scholar
Lee, M. & Moser, R.D. 2019 Spectral analysis of the budget equation in turbulent channel flows at high Reynolds number. J. Fluid Mech. 860, 886–938.CrossRefGoogle Scholar
Long, R.R. & Chen, T. 1981 Experimental evidence for the existence of the ‘mesolayer’ in turbulent systems. J. Fluid Mech. 105, 19–59.CrossRefGoogle Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Time-resolved evolution of coherent structures in turbulent channels: characterization of eddies and cascades. J. Fluid Mech. 759, 432–471.CrossRefGoogle Scholar
Marusic, I. & Kunkel, G.J. 2003 Streamwise turbulence intensity formulation for flat-plate boundary layers. Phys. Fluids 15 (8), 2461–2464.CrossRefGoogle Scholar
Marusic, I., Monty, J.P., Hultmark, M. & Smits, A.J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.CrossRefGoogle Scholar
McKeon, B.J. 2019 Self-similar hierarchies and attached eddies. Phys. Rev. Fluids 4 (8), 082601.CrossRefGoogle Scholar
McKeon, B.J. & Sharma, A.S. 2010 A critical-layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.CrossRefGoogle Scholar
Mizuno, Y. 2016 Spectra of energy transport in turbulent channel flows for moderate Reynolds numbers. J. Fluid Mech. 805, 171–187.CrossRefGoogle Scholar
Moarref, R., Sharma, A.S., Tropp, J.A. & McKeon, B.J. 2013 Model-based scaling of the streamwise energy density in high-Reynolds-number turbulent channels. J. Fluid Mech. 734, 275–316.CrossRefGoogle Scholar
Nedić, J., Vassilicos, J.C. & Ganapathisubramani, B. 2013 Axisymmetric turbulent wakes with new nonequilibrium similarity scalings. Phys. Rev. Lett. 111 (14), 144503.CrossRefGoogle ScholarPubMed
Orr, W.M. 1907 The stability or instability of the steady motions of a perfect liquid and of a viscous liquid. Part I: a perfect liquid. Proc. R. Irish Acad. A 27, 9–68.Google Scholar
Park, J., Hwang, Y. & Cossu, C. 2011 On the stability of large-scale streaks in turbulent Couette and Poiseulle flows. C. R. Méc. 339 (1), 1–5.CrossRefGoogle Scholar
Pujals, G., García-Villalba, M., Cossu, C. & Depardon, S. 2009 A note on optimal transient growth in turbulent channel flows. Phys. Fluids 21 (1), 015109.CrossRefGoogle Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.CrossRefGoogle Scholar
Tomkins, C.D. & Adrian, R.J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.CrossRefGoogle Scholar
Townsend, A.A.R. 1980 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Vadarevu, S.B., Symon, S., Illingworth, S.J. & Marusic, I. 2019 Coherent structures in the linearized impulse response of turbulent channel flow. J. Fluid Mech. 863, 1190–1203.CrossRefGoogle Scholar
Vassilicos, J.C. 2015 Dissipation in turbulent flows. Annu. Rev. Fluid Mech. 47, 95–114.CrossRefGoogle Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9 (4), 883–900.CrossRefGoogle Scholar
Wei, T., Fife, P., Klewicki, J.C. & McMurtry, P. 2005 Properties of the mean momentum balance in turbulent boundary layer, pipe and channel flows. J. Fluid Mech. 522, 303–327.CrossRefGoogle Scholar
Yang, Q., Willis, A.P. & Hwang, Y. 2018 Energy production and self-sustained turbulence at the Kolmogorov scale in Couette flow. J. Fluid Mech. 834, 531–554.CrossRefGoogle Scholar
Yang, Q., Willis, A.P. & Hwang, Y. 2019 Exact coherent states of attached eddies in channel flow. J. Fluid Mech. 862, 1029–1059.CrossRefGoogle Scholar
Zhang, C. & Chernyshenko, S.I. 2016 Quasisteady quasihomogeneous description of the scale interactions in near-wall turbulence. Phys. Rev. Fluids 1 (1), 014401.CrossRefGoogle Scholar