Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-28T22:31:57.610Z Has data issue: false hasContentIssue false
  • English
  • Français

Meridional dynamics of grounded abyssal water masses on a sloping bottom in a mid-latitude 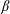$\unicode[STIX]{x1D6FD}$-plane

Published online by Cambridge University Press:  26 February 2018

Gordon E. Swaters Open the ORCID record for Gordon E. Swaters [Opens in a new window]
Get access Rights & Permissions [Opens in a new window]

Abstract

Observations, numerical simulations and theoretical scaling arguments suggest that in mid-latitudes, away from the source regions and the equator, the meridional transport of abyssal water masses along a continental slope corresponds to planetary geostrophic flows that are gravity- or density-driven and topographically steered. We investigate these dynamics using a nonlinear reduced-gravity model that can describe grounded abyssal meridional flow over sloping topography that crosses the planetary vorticity gradient. Exact nonlinear steady and time-dependent solutions are obtained. The general steady theory is illustrated for a non-parallel equatorward flow that possesses a single along-slope grounding along the upslope flank of the current (complementing previous work). Four specific nonlinear time-dependent solutions are described. Two initial-value problems are solved exactly. The first initial configuration corresponds to an equatorward abyssal flow that has no cross-slope shear in the along-slope velocity and possesses a single grounding along the upslope flank of the current. The nonlinear time-dependent evolution of this initial current into a non-parallel shear flow is described. The second initial condition corresponds to an isolated radially symmetric grounded abyssal pool or dome. The nonlinear time-dependent evolution of this abyssal dome, which propagates equatorward with unsteady along- and cross-slope velocities while deforming into an elliptically shaped abyssal dome with 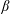$\unicode[STIX]{x1D6FD}$-induced diminishing height, is described. Finally, the nonlinear time-dependent boundary-value problem can be solved exactly in which the in-flow boundary condition on the poleward boundary of the mid-latitude domain corresponds to a time-dependent abyssal current with both an upslope and downslope grounding. Two specific time-dependent boundary conditions are examined. The first corresponds to a time-limited surge in the equatorward volume transport in the abyssal current along the poleward boundary. The second configuration corresponds to the nonlinear evolution of a finite-amplitude downslope plume or loop that forms in the abyssal current that is reminiscent of those seen in baroclinic instability simulations.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Ocean circulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 841 , 25 April 2018 , pp. 674 - 701
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, D. & Killworth, P. D. 1979 Non-linear propagation of long Rossby waves. Deep-Sea Res. 26, 1033–1050.Google Scholar
Armi, L. & D’Asaro, E. 1980 Flow structures of the benthic ocean. J. Geophys. Res. 85 (C1), 469–483.Google Scholar
Baehr, J., Cunnningham, S., Haak, H., Heimbach, P., Kanzow, T. & Marotzke, J. 2009 Observed and simulated estimates of the meridional overturning circulation at 26. 5° N in the Atlantic. Ocean Sci. 5, 575–589.Google Scholar
Choboter, P. G. & Swaters, G. E. 2004 Shallow water modeling of Antarctic Bottom Water crossing the equator. J. Geophys. Res. 109, C03038.Google Scholar
Cunningham, S. A., Kanzow, T., Rayner, D., Baringer, M. O., Johns, W. E., Marotzke, J., Longworth, H. R., Grant, E. M., Hirschi, J. J. M. & Beal, L. M. 2007 Temporal variability of the Atlantic meridional overturning circulation at 26. 5° N. Science 317, 935–938.Google Scholar
Dewar, W. K. 1987 Planetary shock waves. J. Phys. Oceanogr. 17, 470–482.Google Scholar
Edwards, C. A. & Pedlosky, J. 1998 Dynamics of nonlinear cross-equatorial flow. Part I. Potential vorticity transformation. J. Phys. Oceanogr. 28, 2382–2406.Google Scholar
Edwards, N. R., Willmott, A. J. & Killworth, P. D. 1998 On the role of topography and wind stress on the stability of the thermohaline circulation. J. Phys. Oceanogr. 28, 756–778.Google Scholar
Fischer, J. & Schott, F. A. 1997 Seasonal transport variability of the deep western boundary current in the equatorial Atlantic. J. Geophys. Res. 102, 27751–27769.CrossRefGoogle Scholar
Houghton, R. W., Schlitz, R., Beardsley, R. C., Butman, B. & Chamberlin, J. L. 1982 The middle Atlantic bight cool pool: evolution of the temperature structure during summer 1979. J. Phys. Oceanogr. 12, 1019–1029.2.0.CO;2>CrossRefGoogle Scholar
Joyce, T. M., Dunworth-Baker, J., Pickart, R. S. & Waterman, S. 2005 On the deep western boundary current south of Cape Cod. Deep-Sea Res. 52, 615–625.Google Scholar
Kim, A., Swaters, G. E. & Sutherland, B. R. 2014 Cross-equatorial flow of grounded abyssal ocean currents. Geophys. Astrophys. Fluid Dyn. 108, 363–386.Google Scholar
MacCready, P. 1994 Frictional decay of abyssal boundary currents. J. Mar. Res. 52, 197–217.Google Scholar
Nof, D. 1983 The translation of isolated cold eddies on a sloping bottom. Deep-Sea Res. 30, 171–182.Google Scholar
Ou, H. W. & Houghton, R. 1982 A model of the summer progression of the cold-pool temperature in the middle Atlantic bight. J. Phys. Oceanogr. 12, 1030–1036.Google Scholar
Pedlosky, J. 1987 Geophysical Fluid Dynamics. Springer.Google Scholar
Spall, M. A. 1994 Wave-induced abyssal recirculations. J. Mar. Res. 52, 1051–1080.Google Scholar
Swaters, G. E. 1991 On the baroclinic instability of cold-core coupled density fronts on a sloping continental shelf. J. Fluid Mech. 224, 361–382.Google Scholar
Swaters, G. E. 1998 Numerical simulations of the baroclinic dynamics of density-driven coupled fronts and eddies on a sloping bottom. J. Geophys. Res. 103 (C2), 2945–2961.Google Scholar
Swaters, G. E. 2003 Baroclinic characteristics of frictionally destabilized abyssal overflows. J. Fluid Mech. 489, 349–379.Google Scholar
Swaters, G. E. 2006a The meridional flow of source-driven abyssal currents in a stratified basin with topography. Part I. Model development and dynamical characteristics. J. Phys. Oceanogr. 36, 335–355.Google Scholar
Swaters, G. E. 2006b The meridional flow of source-driven abyssal currents in a stratified basin with topography. Part II. Numerical simulation. J. Phys. Oceanogr. 36, 356–375.CrossRefGoogle Scholar
Swaters, G. E. 2009 Mixed bottom-friction–Kelvin–Helmholtz destabilization of source-driven abyssal overflows in the ocean. J. Fluid Mech. 489, 349–379.Google Scholar
Swaters, G. E. 2013 Flow of grounded abyssal ocean currents along zonally-varying topography on a rotating sphere. Geophys. Astrophys. Fluid Dyn. 107, 564–586.Google Scholar
Swaters, G. E. 2015a Midlatitude-equatorial dynamics of a grounded deep western boundary current. Part I. Midlatitude flow and the transition to the equatorial region. J. Phys. Oceanogr. 45, 2457–2469.Google Scholar
Swaters, G. E. 2015b Midlatitude-equatorial dynamics of a grounded deep western boundary current. Part II. Cross-equatorial dynamics. J. Phys. Oceanogr. 45, 2470–2483.CrossRefGoogle Scholar
Swaters, G. E. 2017 Internal dissipative boundary layers in the cross-equatorial flow of a grounded deep western boundary current. Geophys. Astrophys. Fluid Dyn. 111, 91–114.Google Scholar
Swaters, G. E. 2018 Hamiltonian structure and a variational principle for grounded abyssal flow on a sloping bottom in a mid-latitude 𝛽-plane. Stud. Appl. Maths (submitted).CrossRefGoogle Scholar
Wright, D. G. & Willmott, A. J. 1992 Buoyancy driven abyssal circulation in a circumpolar basin. J. Phys. Oceanogr. 22, 139–154.Google Scholar