Article contents
Mechanisms and models of particle drag enhancements in turbulent environments
Published online by Cambridge University Press: 23 March 2023
Abstract
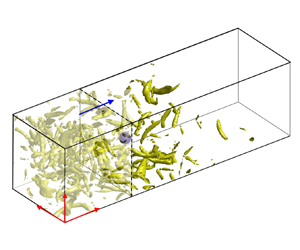
This study conducts direct numerical simulations of free-streaming turbulence passing over individual fixed particles and particle arrays of different number densities. The purpose is to investigate the changes in the mean particle drag due to turbulent environments and the responsible mechanisms. It is confirmed that turbulent environments significantly enhance the particle drag relative to the standard drag in a uniform flow, and the nonlinear dependency of the drag force on the instantaneous incoming flow velocity is insufficient to explain the enhancement. Two mechanisms of particle–turbulence interactions are found to be responsible for the particle drag enhancements. The first mechanism is the enlarged pressure drops on the particle surface, mainly governed by the large scales in turbulent flows. The second mechanism is the increased viscous stresses on the particle surface, dominated by the small scales that enhance the mixing of the low- and high-speed fluids across the particle boundary layer. In terms of quantitative drag enhancement predictions, more general models accounting for the anisotropy of the turbulence are proposed, which fit well with both the simulation data generated in this study and those reported in the literature. Finally, by measuring the drag forces of laminar and turbulent flows passing over arrays of particles, it is found that the overall particle drag increases with decreasing particle–particle relative gap distance. However, the relative enhancement due to turbulence decreases with the particle–particle relative gap distance.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
REFERENCES
- 3
- Cited by



