Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-12-01T02:27:04.475Z Has data issue: false hasContentIssue false
  • English
  • Français

Mechanical energy budget and mixing efficiency for a radiatively heated ice-covered waterbody

Published online by Cambridge University Press:  03 August 2018

Hugo N. Ulloa Open the ORCID record for Hugo N. Ulloa [Opens in a new window] ,
Alfred Wüest  and
Damien Bouffard
Hugo N. Ulloa*
Affiliation:
Physics of Aquatic Systems Laboratory (APHYS) – Margaretha Kamprad Chair, École Polytechnique Fédérale de Lausanne, CH-1014 Lausanne, Switzerland
Alfred Wüest
Affiliation:
Physics of Aquatic Systems Laboratory (APHYS) – Margaretha Kamprad Chair, École Polytechnique Fédérale de Lausanne, CH-1014 Lausanne, Switzerland Eawag, Swiss Federal Institute of Aquatic Science and Technology, Aquatic Physics Group, Department of Surface Waters – Research and Management, Seestrasse 79, CH-6047 Kastanienbaum, Switzerland
Damien Bouffard
Affiliation:
Eawag, Swiss Federal Institute of Aquatic Science and Technology, Aquatic Physics Group, Department of Surface Waters – Research and Management, Seestrasse 79, CH-6047 Kastanienbaum, Switzerland
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Ice-covered waterbodies are far from being quiescent systems. In this paper, we investigate ice-covered freshwater basins heated by solar radiation that penetrates across waters with temperatures below or near the temperature of maximum density. In this scenario, solar radiation sets a radiative buoyancy flux, 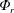$\unicode[STIX]{x1D6F7}_{r}$, that forces increments of temperature/density in the upper fluid volume, which can become gravitationally unstable and drive convection. The goal of this study is twofold. We first focus on formulating the mechanical energy budget, putting emphasis on the conversion of 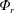$\unicode[STIX]{x1D6F7}_{r}$ to available potential energy, 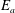$E_{a}$. We find that 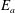$E_{a}$ results from a competition among 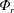$\unicode[STIX]{x1D6F7}_{r}$ and the irreversible mixing controlled by the diapycnal and the laminar mixing rates, respectively. Secondly, and based on the above result, we introduce an integral formulation of the mixing efficiency to quantify the rate of mixing over the relevant time scale $\unicode[STIX]{x1D70F}$, 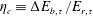$\unicode[STIX]{x1D702}_{c}\equiv \unicode[STIX]{x0394}E_{b,\unicode[STIX]{x1D70F}}/E_{r,\unicode[STIX]{x1D70F}}$, where 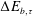$\unicode[STIX]{x0394}E_{b,\unicode[STIX]{x1D70F}}$ and 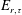$E_{r,\unicode[STIX]{x1D70F}}$ are the change of background potential energy and the time-integrated 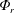$\unicode[STIX]{x1D6F7}_{r}$ over $\unicode[STIX]{x1D70F}$. The above definition is applied to estimate 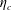$\unicode[STIX]{x1D702}_{c}$ for the first time, finding an approximate value of 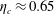$\unicode[STIX]{x1D702}_{c}\approx 0.65$. This result suggests that radiatively heated ice-covered waterbodies might be subject to high mixing rates. Overall, the present work provides a framework to examine energetics and mixing in ice-covered waters.

JFM classification

Convection: Convection in cavities Geophysical and Geological Flows: Ice sheets Mixing: Turbulent mixing
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 852 , 10 October 2018 , R1
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barkan, R., Winters, K. & Llewellyn Smith, S. 2013 Rotating horizontal convection. J. Fluid Mech. 723, 556–586.Google Scholar
Bouffard, D., Zdorovennova, G., Bogdanov, S., Efremova, T., Lavanchy, S., Palshin, N., Terzhevik, A., Råman Vinnå, L., Volkov, S., Wüest, A., Zdorovennov, R. & Ulloa, H. N. 2018 How to quantify under-ice convection dynamics in lakes. Implication for life under the ice. Inland Waters (accepted under revision).Google Scholar
Bouffard, D., Zdorovennov, R. E., Zdorovennova, G. E., Pasche, N., Wüest, A. & Terzhevik, A. Y. 2016 Ice-covered Lake Onega: effects of radiation on convection and internal waves. Hydrobiologia 780 (1), 21–36.Google Scholar
Davies Wykes, M. & Dalziel, S. 2014 Efficient mixing in stratified flows: experimental study of a Rayleigh–Taylor unstable interface within an otherwise stable stratification. J. Fluid Mech. 756, 1027–1057.Google Scholar
Davies Wykes, M., Hughes, G. & Dalziel, S. 2015 On the meaning of mixing efficiency for buoyancy-driven mixing in stratified turbulent flows. J. Fluid Mech. 781, 261–275.Google Scholar
Farmer, D. M. 1975 Penetrative convection in the absence of mean shear. Q. J. R. Meteorol. Soc. 101 (430), 869–891.Google Scholar
Forrest, A. L., Laval, B. E., Pieters, R. & Lim, D. S. S. 2013 A cyclonic gyre in an ice-covered lake. Limnol. Oceanogr. 58 (1), 363–375.Google Scholar
Gayen, B., Griffiths, R. & Hughes, G. 2014 Stability transitions and turbulence in horizontal convection. J. Fluid Mech. 751, 698–724.Google Scholar
Gregg, M. C., D’Asaro, E. A., Riley, J. J. & Kunze, E. 2018 Mixing efficiency in the ocean. Annu. Rev. Mar. Sci. 10 (1), 443–473.Google Scholar
Hughes, G., Gayen, B. & Griffiths, R. 2013 Available potential energy in Rayleigh–Bénard convection. J. Fluid Mech. 729.Google Scholar
Jonas, T., Terzhevik, A. Y., Mironov, D. V. & Wüest, A. 2003 Radiatively driven convection in an ice-covered lake investigated by using temperature microstructure technique. J. Geophys. Res. 108, 3183.Google Scholar
Kirillin, G. B., Forrest, A. L., Graves, K. E., Fischer, A., Engelhardt, C. & Laval, B. E. 2015 Axisymmetric circulation driven by marginal heating in ice-covered lakes. Geophys. Res. Lett. 42 (8), 2893–2900.Google Scholar
Kirillin, G., Leppäranta, M., Terzhevik, A., Granin, N., Bernhardt, J., Engelhardt, C., Efremova, T., Golosov, S., Palshin, N., Sherstyankin, P., Zdorovennova, G. & Zdorovennov, R. 2012 Physics of seasonally ice-covered lakes: a review. Aquat. Sci. 74 (4), 659–682.Google Scholar
MacKay, M. D., Verseghy, D. L., Fortin, V. & Rennie, M. D. 2017 Wintertime simulations of a boreal lake with the Canadian Small Lake Model. J. Hydrometeorol. 18 (8), 2143–2160.Google Scholar
Manins, P. C. & Turner, J. S. 1978 The relation between the flux ratio and energy ratio in convectively mixed layers. Q. J. R. Meteorol. Soc. 104 (439), 39–44.Google Scholar
Mashayek, A., Salehipour, H., Bouffard, D., Caulfield, C. P., Ferrari, R., Nikurashin, M., Peltier, W. R. & Smyth, W. D. 2017 Efficiency of turbulent mixing in the abyssal ocean circulation. Geophys. Res. Lett. 44 (12), 6296–6306.Google Scholar
Mironov, D., Terzhevik, A., Kirillin, G., Jonas, T., Malm, J. & Farmer, D. 2002 Radiatively driven convection in ice-covered lakes: observations, scaling, and a mixed layer model. J. Geophys. Res. 107 (C4), 3032.Google Scholar
Peltier, W. R. & Caulfield, C. P. 2003 Mixing efficiency in stratified shear flows. Annu. Rev. Fluid Mech. 35 (1), 135–167.Google Scholar
Rizk, W., Kirillin, G. & Leppäranta, M. 2014 Basin-scale circulation and heat fluxes in ice-covered lakes. Limnol. Oceanogr. 59 (2), 445–464.Google Scholar
Salonen, K., Pulkkanen, M., Salmi, P. & Griffiths, R. W. 2014 Interannual variability of circulation under spring ice in a boreal lake. Limnol. Oceanogr. 59 (6), 2121–2132.Google Scholar
Sohail, T., Gayen, B. & Hogg, A. M. 2018 Convection enhances mixing in the Southern Ocean. Geophys. Res. Lett. 45 (9), 4198–4207.Google Scholar
Tailleux, R. 2009 On the energetics of stratified turbulent mixing, irreversible thermodynamics, Boussinesq models and the ocean heat engine controversy. J. Fluid Mech. 638, 339–382.Google Scholar
Vreugdenhil, C. A., Gayen, B. & Griffiths, R. W. 2016 Mixing and dissipation in a geostrophic buoyancy-driven circulation. J. Geophys. Res. 121 (8), 6076–6091.Google Scholar
Wells, M. G. & Sherman, B. 2001 Stratification produced by surface cooling in lakes with significant shallow regions. Limnol. Oceanogr. 46 (7), 1747–1759.Google Scholar
Winters, K., Lombard, P., Riley, J. & D’Asaro, E. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 289, 115–128.Google Scholar
Wüest, A. & Lorke, A. 2003 Small-scale hydrodynamics in lakes. Annu. Rev. Fluid Mech. 35 (1), 373–412.Google Scholar
Yang, B., Young, J., Brown, L. & Wells, M. 2017 High-frequency observations of temperature and dissolved oxygen reveal under-ice convection in a large lake. Geophys. Res. Lett. 44 (24), 12218–12226.Google Scholar