Hostname: page-component-599cfd5f84-v8j7l Total loading time: 0 Render date: 2025-01-07T08:01:07.341Z Has data issue: false hasContentIssue false
  • English
  • Français

Measurement of negative thermophoretic force

Published online by Cambridge University Press:  19 September 2016

Ryan W. Bosworth ,
A. L. Ventura ,
A. D. Ketsdever  and
S. F. Gimelshein
Ryan W. Bosworth
Affiliation:
Department of Mechanical and Aerospace Engineering, University of Colorado – Colorado Springs, Colorado Springs, CO 80918, USA
A. L. Ventura
Affiliation:
Department of Mechanical and Aerospace Engineering, University of Colorado – Colorado Springs, Colorado Springs, CO 80918, USA
A. D. Ketsdever*
Affiliation:
Department of Mechanical and Aerospace Engineering, University of Colorado – Colorado Springs, Colorado Springs, CO 80918, USA
S. F. Gimelshein
Affiliation:
Gimel Inc., 2417 Carol Park Place, Montrose, CA 91020, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

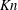The rarefied gas flow phenomenon of thermophoresis is studied experimentally on a macroscopic spherical particle with a diameter of 5.1 cm for pressures ranging from 0.01 to 10 Pa (Knudsen numbers $Kn$ from 10 to 0.01, respectively). Size scaling with matching Knudsen numbers makes the results applicable to microscale particles such as aerosol droplets at atmospheric pressure. Two sets of measurements are presented. The first set, complemented by numerical modelling based on the solution of the ellipsoidal statistical Bhatnagar–Gross–Krook kinetic equation, is focused on a spherical particle of high thermal conductivity in close proximity to a heated wall. The second set is conducted for the same particle placed in a linear thermal gradient established between two parallel walls. Results show the first reproducible measurements of negative thermophoretic force acting on a spherical particle in the direction from cold to hot, with values of the order of 5 % of the maximum hot to cold force production.

JFM classification

Rarefied Gas Flow: Kinetic theory Rarefied Gas Flow: Molecular dynamics Rarefied Gas Flow: Rarefied Gas Flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 805 , 25 October 2016 , pp. 207 - 221
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bakanov, S. P. & Deryagin, B. V. 1959 On the theory of thermal precipitation of highly disperse aerosol systems. Kolloidn. Z. 21 (4), 377–384.Google Scholar
Beresnev, S. & Chernyak, V. 1995 Thermophoresis of a spherical particle in a rarefied gas: numerical analysis based on the model kinetic equations. Phys. Fluids 7 (7), 1743–1756.Google Scholar
Cercignani, C. 1975 Theory and Application of the Boltzmann Equation. Scottish Academic Press.Google Scholar
Crookes, W. 1874 On attraction and repulsion resulting from radiation. Phil. Trans. R. Soc. Lond. 164, 501–527.Google Scholar
Dwyer, H. A. 1967 Thirteen-moment theory of the thermal force on a spherical particle. Phys. Fluids 10 (5), 976–984.Google Scholar
Epstein, P. S. 1929 Zur Theorie des Radiometers. Z. Phys. A 54 (7–8), 537–563.Google Scholar
Gallis, M. A., Torczynski, J. R. & Rader, D. J. 2001 An approach for simulating the transport of spherical particles in a rarefied gas flow via the direct simulation Monte Carlo method. Phys. Fluids 13 (11), 3482–3492.Google Scholar
Ivanov, M. S., Markelov, G. N., Gimelshein, S. F., Mishina, L. V., Krylov, A. N. & Grechko, N. V. 1998 High-altitude capsule aerodynamics with real gas effects. J. Spacecr. Rockets 35 (1), 16–22.Google Scholar
Jamison, A. J., Ketsdever, A. D. & Muntz, E. P. 2002 Gas dynamic calibration of a nano-newton thrust stand. Rev. Sci. Instrum. 73 (10), 3629–3637.Google Scholar
Ketsdever, A., Gimelshein, N., Gimelshein, S. & Selden, N. 2012 Radiometric phenomena: from the 19th to the 21st century. Vacuum 86 (11), 1644–1662.Google Scholar
Li, W. & Davis, E. J. 1995 The effects of gas and particle properties on thermophoresis. Science 26 (7), 1085–1099.Google Scholar
Loyalka, S. K. 1971 Kinetic theory of thermal transpiration and mechanocaloric effect. I. J. Chem. Phys. 55 (9), 4497–4503.Google Scholar
Loyalka, S. K. 1992 Thermophoretic force on a single particle. I: numerical solution of the linearized Boltzmann equation. J. Aero. Sci. 23 (3), 291–300.Google Scholar
Maxwell, J. C. 1879 On stresses in rarified gases arising from inequalities of temperature. Phil. Trans. R. Soc. Lond. 11, 231–256.Google Scholar
Mieussens, L. 2000 Discrete-velocity models and numerical schemes for the Boltzmann–BGK equation in plane and axisymmetric geometries. J. Comput. Phys. 162 (2), 429–466.Google Scholar
Onishi, Y. 1972 Effect of accommodation coefficient on thermal creep flow of rarefied gas. Trans. Japan. Soc. Aeronaut. Space Sci. 15 (29), 117–123.Google Scholar
Phillips, W. F. 1972 Thermal force on spherical particles in a rarefied gas. Phys. Fluids 15 (1972), 999–1003.Google Scholar
Selden, N., Ngalande, C., Gimelshein, N., Gimelshein, S. & Ketsdever, A. 2009a Origins of radiometric forces on a circular vane with a temperature gradient. J. Fluid Mech. 634, 419–431.Google Scholar
Selden, N., Ngalande, C., Gimelshein, S., Muntz, E. P., Alexeenko, A. & Ketsdever, A. 2009b Area and edge effects in radiometric forces. Phys. Rev. E 79 (4), 1–6.Google Scholar
Sharipov, F. 2015 Rarefied Gas Dynamics: Fundamentals for Research and Practice. Wiley.Google Scholar
Sone, Y. 1972 A flow induced by thermal stress in rarefied gas. J. Phys. Soc. Japan 33 (1), 232–236.Google Scholar
Sone, Y. & Aoki, K. 1977 Forces on a spherical particle in a slightly rarefied gas. Prog. Astronaut. Aeronaut. 51, 417–433.Google Scholar
Sone, Y. & Aoki, K. 1981 Negative thermophoresis: thermal stress slip flow around a spherical particle in a rarefied gas. In Rarefied Gas Dynamics; International Symposium (ed. Fisher, S. S.), pp. 489–503. American Institute of Aeronautics and Astronautics.Google Scholar
Sone, Y. & Aoki, K. 1983 A similarity solution of the linearized Boltzmann equation with application to thermophoresis of a spherical particle. J. Méc. Théor. Appl. 2, 3–12.Google Scholar
Takata, S., Aoki, K. & Sone, Y. 1994 Thermophoresis of a sphere with a uniform temperature: numerical analysis of the Boltzmann equation for hard-sphere molecules. In Rarefied Gas Dynamics: Theory and Simulations (ed. Weaver, D. P. & Shizgal, B. D.), Progress in Astronautics and Aeronautics, vol. 159, pp. 626–639. AIAA.Google Scholar
Tyndall, J. 1870 On dust and disease. Proc. R. Inst. 6, 3.Google Scholar
Ventura, A., Gimelshein, N., Gimelshein, S. & Ketsdever, A. 2013 Effect of vane thickness on radiometric force. J. Fluid Mech. 735, 684–704.Google Scholar
Ventura, A., Ketsdever, A., Webb, R., Alexeenko, A., Gimelshein, N. & Gimelshein, S. 2012 Repulsion and attraction caused by radiometric forces. In Rarefied Gas Dynamics (ed. Mareschal, M. & Santos, A.), AIP Conf. Proc., vol. 1501, pp. 727–734. American Institute of Physics.Google Scholar
Wadsworth, D. C., Gimelshein, N. E., Gimelshein, S. F. & Wysong, I. J. 2008 Assessment of translational anisotropy in rarefied flows using kinetic approaches. In Rarefied Gas Dynamics (ed. Abe, T.), AIP Conf. Proc., vol. 1084, pp. 206–211. American Institute of Physics.Google Scholar
Waldmann, L. 1959 Über die Kraft eines inhomogenen Gases auf kleine suspendierte Kugeln. Z. Naturforsch. 14 (A), 589–599.Google Scholar
Yamamoto, K. & Ishihara, Y. 1988 Thermophoresis of a spherical particle in a rarefied gas of a transition regime. Phys. Fluids 31 (12), 3618–3624.Google Scholar
Young, J. B. 2011 Thermophoresis of a spherical particle: reassessment, clarification, and new analysis. Aerosol Sci. Technol. 45 (8), 927–948.Google Scholar
Zheng, F. 2002 Thermophoresis of spherical and non-spherical particles: a review of theories and experiments. Adv. Colloid Interface Sci. 97, 255–278.Google Scholar