Article contents
Mean flow stability analysis of oscillating jet experiments
Published online by Cambridge University Press: 19 September 2014
Abstract
Linear stability analysis (LSA) is applied to the mean flow of an oscillating round jet with the aim of investigating the robustness and accuracy of mean flow stability wave models. The jet’s axisymmetric mode is excited at the nozzle lip through a sinusoidal modulation of the flow rate at amplitudes ranging from 0.1 % to 100 %. The instantaneous flow field is measured via particle image velocimetry (PIV) and decomposed into a mean and periodic part utilizing proper orthogonal decomposition (POD). Local LSA is applied to the measured mean flow adopting a weakly non-parallel flow approach. The resulting global perturbation field is carefully compared with the measurements in terms of spatial growth rate, phase velocity, and phase and amplitude distribution. It is shown that the stability wave model accurately predicts the excited flow oscillations during their entire growth phase and during a large part of their decay phase. The stability wave model applies over a wide range of forcing amplitudes, showing no pronounced sensitivity to the strength of nonlinear saturation. The upstream displacement of the neutral point and the successive reduction of gain with increasing forcing amplitude is very well captured by the stability wave model. At very strong forcing (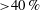 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{>}40\, \%$), the flow becomes essentially stable to the axisymmetric mode. For these extreme cases, the prediction deteriorates from the measurements due to an interaction of the forced wave with the geometric confinement of the nozzle. Moreover, the model fails far downstream in a region where energy is transferred from the oscillation back to the mean flow. This study supports previously conducted mean flow stability analysis of self-excited flow oscillations in the cylinder wake and in the vortex breakdown bubble and extends the methodology to externally forced convectively unstable flows. The high accuracy of mean flow stability wave models as demonstrated here is of great importance for the analysis of coherent structures in turbulent shear flows.
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{>}40\, \%$), the flow becomes essentially stable to the axisymmetric mode. For these extreme cases, the prediction deteriorates from the measurements due to an interaction of the forced wave with the geometric confinement of the nozzle. Moreover, the model fails far downstream in a region where energy is transferred from the oscillation back to the mean flow. This study supports previously conducted mean flow stability analysis of self-excited flow oscillations in the cylinder wake and in the vortex breakdown bubble and extends the methodology to externally forced convectively unstable flows. The high accuracy of mean flow stability wave models as demonstrated here is of great importance for the analysis of coherent structures in turbulent shear flows.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 44
- Cited by


