Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-08T02:26:05.076Z Has data issue: false hasContentIssue false
  • English
  • Français

Maximum drop radius and critical Weber number for splashing in the dynamical Leidenfrost regime

Published online by Cambridge University Press:  30 August 2016

Guillaume Riboux  and
José Manuel Gordillo
Guillaume Riboux*
Affiliation:
Área de Mecánica de Fluidos, Departamento de Ingeniería Aeroespacial y Mecánica de Fluidos, Universidad de Sevilla, Avenida de los Descubrimientos s/n 41092, Sevilla, Spain
José Manuel Gordillo
Affiliation:
Área de Mecánica de Fluidos, Departamento de Ingeniería Aeroespacial y Mecánica de Fluidos, Universidad de Sevilla, Avenida de los Descubrimientos s/n 41092, Sevilla, Spain
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

At room temperature, when a drop impacts against a smooth solid surface at a velocity above the so-called critical velocity for splashing, the drop loses its integrity and fragments into tiny droplets violently ejected radially outwards. Below this critical velocity, the drop simply spreads over the substrate. 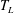Splashing is also reported to occur for solid substrate temperatures above the Leidenfrost temperature, $T_{L}$, for which a vapour layer prevents the drop from touching the solid. In this case, the splashing morphology differs from the one reported at room temperature because, thanks to the presence of the gas layer, the shear stresses acting on the liquid can be neglected. Our purpose here is to predict, for wall temperatures above 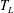$T_{L}$, the critical Weber number for splashing as well as the maximum spreading radius. First, making use of boundary integral simulations, we calculate both the time evolution of the liquid velocity as well as the height of the sheet which is ejected tangentially to the substrate. These results are then used as boundary conditions for the one-dimensional mass and momentum equations describing the dynamics of the rim limiting the expanding liquid sheet. Our predictions for both the maximum spreading radius and for the critical Weber number for splashing are in good agreement with experimental observations.

JFM classification

Drops and Bubbles: Breakup/coalescence Drops and Bubbles: Drops and Bubbles Drops and Bubbles: Drops
Type
Papers
Information
Journal of Fluid Mechanics , Volume 803 , 25 September 2016 , pp. 516 - 527
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agbaglah, G., Josserand, C. & Zaleski, S. 2013 Longitudinal instability of a liquid rim. Phys. Fluids 25, 022103.CrossRefGoogle Scholar
Culick, F. E. C. 1960 Comments on a ruptured soap film. J. Appl. Phys. 31 (1274), 1128–1129.CrossRefGoogle Scholar
Duez, C., Ybert, C., Clanet, C. & Bocquet, L. 2007 Making a splash with water repellency. Nat. Phys. 3, 180–183.CrossRefGoogle Scholar
Eggers, J., Fontelos, M. A., Josserand, C. & Zaleski, S. 2010 Drop dynamics after impact on a solid wall: theory and simulations. Phys. Fluids 22 (6), 062101.CrossRefGoogle Scholar
Eggers, J. & Villermaux, E. 2008 Physics of liquid jets. Rep. Prog. Phys. 71, 036601.CrossRefGoogle Scholar
Gordillo, J. M. & Gekle, S. 2010 Generation and breakup of worthington jets after cavity collapse. Part 2. Tip breakup of stretched jets. J. Fluid Mech. 663, 193–330.CrossRefGoogle Scholar
Josserand, C. & Thoroddsen, S. T. 2016 Drop impact on a solid surface. Annu. Rev. Fluid Mech. 48, 365–391.CrossRefGoogle Scholar
Lastakowski, H., Boyer, F., Biance, A.-L., Pirat, C. & Ybert, C. 2014 Bridging local to global dynamics of drop impact onto solid substrates. J. Fluid Mech. 747, 103–118.CrossRefGoogle Scholar
Riboux, G. & Gordillo, J. M. 2014 Experiments of drops impacting a smooth solid surface: a model of the critical impact speed for drop splashing. Phys. Rev. Lett. 113, 024507.Google Scholar
Riboux, G. & Gordillo, J. M. 2015 The diameters and velocities of the droplets ejected after splashing. J. Fluid Mech. 772, 630–648.CrossRefGoogle Scholar
Rodríguez–Rodríguez, J., Gordillo, J. M. & Martínez–Bazán, C. 2006 Breakup time and morphology of drops and bubbles in a high-Reynolds-number flow. J. Fluid Mech. 548, 69–86.CrossRefGoogle Scholar
Roisman, I. V. 2009 Inertia dominated drop collisions. Part II. An analytical solution of the Navier–Stokes equations for a spreading viscous film. Phys. Fluids 21, 052104.CrossRefGoogle Scholar
Shirota, M., van Limbeek, M. J., Sun, C., Prosperetti, A. & Lohse, D. 2016 Dynamic Leidenfrost effect: relevant time- and length-scales. Phys. Rev. Lett. 116, 064501.CrossRefGoogle ScholarPubMed
Staat, H. J. J., Tran, T., Geerdink, B., Riboux, G., Sun, C., Gordillo, J. M. & Lohse, D. 2015 Phase diagram for droplet impact on superheated surfaces. J. Fluid Mech. 779 (R3), 1–12.CrossRefGoogle Scholar
Taylor, G. I. 1959 The dynamics of thin sheets of fluid. Part II. Waves on fluid sheets. Proc. R. Soc. Lond. A 253 (1274), 296–312.Google Scholar
Tran, T., Staat, H. J. J., Susarrey–Arce, A., Foertsch, T. C., van Houselt, A., Gardeniers, H. J. G. E., Prosperetti, A., Lohse, D. & Sun, C. 2013 Droplet impact on superheated micro-structured surfaces. Soft Matt. 9, 3272–3282.CrossRefGoogle Scholar
Tran, T., Staat, H. J. J., Prosperetti, A., Sun, C. & Lohse, D. 2012 Drop impact on superheated surfaces. Phys. Rev. Lett. 108, 036101.CrossRefGoogle ScholarPubMed
Villermaux, E. & Bossa, B. 2011 Drop fragmentation on impact. J. Fluid Mech. 668, 412–435.CrossRefGoogle Scholar
Wagner, H. 1932 Phenomena associated with impacts and sliding on liquid surfaces. Z. Angew. Math. Mech. 12, 193–215.CrossRefGoogle Scholar
Wilderman, H., Visser, C. W., Sun, C. & Lohse, D. 2016 On the spreading of impacting drops. J. Fluid Mech. (submitted) arXiv:1602.03782.Google Scholar
Xu, L., Zhang, W. W & Nagel, S. R. 2005 Drop splashing on a dry smooth surface. Phys. Rev. Lett. 94, 184505.CrossRefGoogle ScholarPubMed