Hostname: page-component-669899f699-ggqkh Total loading time: 0 Render date: 2025-04-26T09:48:27.273Z Has data issue: false hasContentIssue false
  • English
  • Français

Mapping the properties of wake-induced vibration on a circular cylinder

Published online by Cambridge University Press:  13 December 2024

Ke Lin Open the ORCID record for Ke Lin [Opens in a new window] ,
Yuankun Sun ,
Hongyuan Liu ,
Yunpeng Zhu ,
Jiasong Wang ,
Michael S. Triantafyllou Open the ORCID record for Michael S. Triantafyllou [Opens in a new window]  and
Dixia Fan Open the ORCID record for Dixia Fan [Opens in a new window]
Ke Lin
Affiliation:
Department of Engineering Mechanics, School of Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, PR China
Yuankun Sun
Affiliation:
Ocean University of China, College of Engineering, Qingdao 266100, PR China
Hongyuan Liu
Affiliation:
Zhejiang University-Westlake University Joint Training, Zhejiang University, Hangzhou 310027, PR China Key Laboratory of Coastal Environment and Resources of Zhejiang Province, School of Engineering, Westlake University, Hangzhou, Zhejiang 310030, PR China
Yunpeng Zhu
Affiliation:
Zhejiang University-Westlake University Joint Training, Zhejiang University, Hangzhou 310027, PR China Key Laboratory of Coastal Environment and Resources of Zhejiang Province, School of Engineering, Westlake University, Hangzhou, Zhejiang 310030, PR China
Jiasong Wang*
Affiliation:
Department of Engineering Mechanics, School of Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, PR China Key Laboratory of Hydrodynamics of Ministry of Education, Shanghai Jiao Tong University, Shanghai 200240, PR China
Michael S. Triantafyllou
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute Technology, Cambridge, MA 02139, USA
Dixia Fan*
Affiliation:
Key Laboratory of Coastal Environment and Resources of Zhejiang Province, School of Engineering, Westlake University, Hangzhou, Zhejiang 310030, PR China Institute of Advanced Technology, Westlake Institute for Advanced Study, Hangzhou, Zhejiang 310024, PR China
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

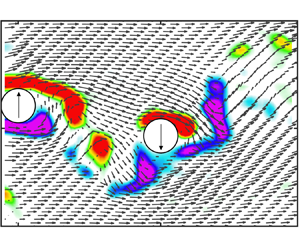
This study conducts experimental investigations into wake-induced vibration (WIV) of a circular cylinder placed downstream of an oscillating cylinder. Surprisingly, it is observed that the previously identified WIV phenomenon, characterized by a sustained increase in amplitude at higher reduced velocities, does not occur when the upstream cylinder oscillates at large amplitudes. Instead, a different phenomenon, which we refer to as the ‘wake-captured vibration’, becomes dominant. The experiments reveal a negative correlation between the vortex-induced vibration amplitude response of the upstream cylinder and the WIV amplitude response of the downstream cylinder. Through a quasi-steady and linear instability analysis, the study demonstrates that the previously proposed wake-displacement mechanism may not be applicable for predicting the cylinder WIV response in the wake of an oscillating body. This is because the lift force gradients across the wake, measured through stationary cylinder experiments, decrease significantly when the upstream cylinder vibrates at higher amplitudes. Consequently, actively controlled vibration experiments are conducted to systematically map the hydrodynamic properties of the downstream cylinder vibrating in the wake of an oscillating cylinder. The findings align with observations from free-vibration experiments, and help to explain the amplitude and frequency response of WIV. Additionally, wake visualization through particle image velocimetry is conducted to provide further insights into the complex wake and vortex–body interactions.

JFM classification

Aerodynamics: Flow-structure interactions Vortex Flows: Vortex shedding Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1001 , 25 December 2024 , A33
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Armin, M., Khorasanchi, M. & Day, S. 2018 Wake interference of two identical oscillating cylinders in tandem: an experimental study. Ocean Engng 166, 311–323.CrossRefGoogle Scholar
Assi, G.R.S., Bearman, P.W., Carmo, B.S., Meneghini, J.R., Sherwin, S.J. & Willden, R.H.J. 2013 The role of wake stiffness on the wake-induced vibration of the downstream cylinder of a tandem pair. J. Fluid Mech. 718, 210–245.CrossRefGoogle Scholar
Assi, G.R.S., Bearman, P.W. & Meneghini, J.R. 2010 On the wake-induced vibration of tandem circular cylinders: the vortex interaction excitation mechanism. J. Fluid Mech. 661, 365–401.CrossRefGoogle Scholar
Bao, Y., Huang, C., Zhou, D., Tu, J. & Han, Z. 2012 Two-degree-of-freedom flow-induced vibrations on isolated and tandem cylinders with varying natural frequency ratios. J. Fluids Struct. 35, 50–75.CrossRefGoogle Scholar
Bokaian, A. & Geoola, F. 1984 Wake-induced galloping of two interfering circular cylinders. J. Fluid Mech. 146, 383–415.CrossRefGoogle Scholar
Borazjani, I. & Sotiropoulos, F. 2009 Vortex-induced vibrations of two cylinders in tandem arrangement in the proximity-wake interference region. J. Fluid Mech. 621, 321–364.CrossRefGoogle ScholarPubMed
Brika, D. & Laneville, A. 1999 The flow interaction between a stationary cylinder and a downstream flexible cylinder. J. Fluids Struct. 13 (5), 579–606.CrossRefGoogle Scholar
Carberry, J., Sheridan, J. & Rockwell, D. 2005 Controlled oscillations of a cylinder: forces and wake modes. J. Fluid Mech. 538, 31–69.CrossRefGoogle Scholar
Den Hartog, J.P. 1985 Mechanical Vibrations. Courier Corporation.Google Scholar
Fan, D. & Triantafyllou, M.S. 2022 Vortex-induced forces of crossflow and inline oscillating bluff bodies at moderate Reynolds numbers. Mar. Struct. 86, 103305.CrossRefGoogle Scholar
Fan, D., Wang, Z., Triantafyllou, M.S. & Karniadakis, G.E. 2019 Mapping the properties of the vortex-induced vibrations of flexible cylinders in uniform oncoming flow. J. Fluid Mech. 881, 815–858.CrossRefGoogle Scholar
Granger, S. & Païdoussis, M.P. 1996 An improvement to the quasi-steady model with application to cross-flow-induced vibration of tube arrays. J. Fluid Mech. 320, 163–184.CrossRefGoogle Scholar
Griffith, M.D., Jacono, D.L., Sheridan, J. & Leontini, J.S. 2017 Flow-induced vibration of two cylinders in tandem and staggered arrangements. J. Fluid Mech. 833, 98–130.CrossRefGoogle Scholar
Hover, F.S. & Triantafyllou, M.S. 2001 Galloping response of a cylinder with upstream wake interference. J. Fluids Struct. 15 (3–4), 503–512.CrossRefGoogle Scholar
Hu, Z., Wang, J. & Sun, Y. 2020 a Cross-flow vibrations of two identical elastically mounted cylinders in tandem arrangement using wind tunnel experiment. Ocean Engng 209, 107501.CrossRefGoogle Scholar
Hu, Z., Wang, J. & Sun, Y. 2020 b Flow-induced vibration of one-fixed-one-free tandem arrangement cylinders with different mass-damping ratios using wind tunnel experiment. J. Fluids Struct. 96, 103019.CrossRefGoogle Scholar
Jing, H., Huang, F., He, X. & Cai, C. 2021 Wake-induced vibrations of tandem flexible cable models in a wind tunnel. Ocean Engng 233, 109188.CrossRefGoogle Scholar
Khalak, A. & Williamson, C.H.K. 1997 Investigation of relative effects of mass and damping in vortex-induced vibration of a circular cylinder. J. Wind Engng Ind. Aerodyn. 69, 341–350.CrossRefGoogle Scholar
Kim, S., Alam, M.M., Sakamoto, H. & Zhou, Y. 2009 Flow-induced vibrations of two circular cylinders in tandem arrangement, part 1: characteristics of vibration. J. Wind Engng Ind. Aerodyn. 97 (5–6), 304–311.CrossRefGoogle Scholar
Lam, K.M. & To, A.P. 2003 Interference effect of an upstream larger cylinder on the lock-in vibration of a flexibly mounted circular cylinder. J. Fluids Struct. 17 (8), 1059–1078.CrossRefGoogle Scholar
Lin, K., Fan, D. & Wang, J. 2020 a Dynamic response and hydrodynamic coefficients of a cylinder oscillating in crossflow with an upstream wake interference. Ocean Engng 209, 107520.CrossRefGoogle Scholar
Lin, K., Wang, J., Fan, D. & Triantafyllou, M.S. 2021 Flow-induced cross-flow vibrations of long flexible cylinder with an upstream wake interference. Phys. Fluids 33 (6), 065104.CrossRefGoogle Scholar
Lin, K., Wang, J., Zheng, H. & Sun, Y. 2020 b Numerical investigation of flow-induced vibrations of two cylinders in tandem arrangement with full wake interference. Phys. Fluids 32 (1), 015112.CrossRefGoogle Scholar
Ma, L., Lin, K., Fan, D., Wang, J. & Triantafyllou, M.S. 2022 Flexible cylinder flow-induced vibration. Phys. Fluids 34 (1), 011302.CrossRefGoogle Scholar
Novak, M. 1972 Galloping oscillations of prismatic structures. J. Engng Mech. ASCE 98 (1), 27–46.Google Scholar
Païdoussis, M.P., Price, S.J. & De Langre, E. 2010 Fluid–Structure Interactions: Cross-Flow-Induced Instabilities. Cambridge University Press.CrossRefGoogle Scholar
Papaioannou, G.V., Yue, D.K.P., Triantafyllou, M.S. & Karniadakis, G.E. 2008 On the effect of spacing on the vortex-induced vibrations of two tandem cylinders. J. Fluids Struct. 24 (6), 833–854.CrossRefGoogle Scholar
Prasanth, T.K. & Mittal, S. 2009 Flow-induced oscillation of two circular cylinders in tandem arrangement at low $Re$. J. Fluids Struct. 25 (6), 1029–1048.CrossRefGoogle Scholar
Price, S.J. & Païdoussis, M.P. 1984 An improved mathematical model for the stability of cylinder rows subject to cross-flow. J. Sound Vib. 97 (4), 615–640.CrossRefGoogle Scholar
Price, S.J., Païdoussis, M.P. & Al-Jabir, A.M. 1993 Current-induced fluidelastic instabilities of a multi-tube flexible riser: theoretical results and comparison with experiments. J. Offshore Mech. Arct. Eng. 115 (4), 206–212.CrossRefGoogle Scholar
Qin, B., Alam, M.M. & Zhou, Y. 2017 Two tandem cylinders of different diameters in cross-flow: flow-induced vibration. J. Fluid Mech. 829, 621–658.CrossRefGoogle Scholar
Qin, B., Alam, M.M. & Zhou, Y. 2019 Free vibrations of two tandem elastically mounted cylinders in crossflow. J. Fluid Mech. 861, 349–381.CrossRefGoogle Scholar
Ruscheweyh, H.P. 1983 Aeroelastic interference effects between slender structures. J. Wind Engng Ind. Aerodyn. 14 (1–3), 129–140.CrossRefGoogle Scholar
Sharma, G. & Bhardwaj, R. 2023 Flow-induced vibrations of elastically coupled tandem cylinders. J. Fluid Mech. 976, A22.CrossRefGoogle Scholar
Soares, B. & Srinil, N. 2021 Modelling of wake-induced vibrations of tandem cylinders with a nonlinear wake-deficit oscillator. J. Fluids Struct. 105, 103340.CrossRefGoogle Scholar
Sun, H., Li, H., Yang, N., Hou, G. & Bernitsas, M.M. 2023 Experimental and numerical study of the shielding effect of two tandem rough cylinders in flow-induce oscillation. Mar. Struct. 89, 103374.CrossRefGoogle Scholar
Wang, J., Fan, D. & Lin, K. 2020 A review on flow-induced vibration of offshore circular cylinders. J. Hydrodyn. 32 (3), 415–440.CrossRefGoogle Scholar
Wang, J., Zhang, Y., Hu, G. & Zhang, W. 2023 Wake-induced vibration and heat transfer characteristics of three tandem semi-circular cylinders. J. Fluids Struct. 123, 104004.CrossRefGoogle Scholar
Wang, L., Alam, M.M. & Zhou, Y. 2018 Two tandem cylinders of different diameters in cross-flow: effect of an upstream cylinder on wake dynamics. J. Fluid Mech. 836, 5–42.CrossRefGoogle Scholar
Wang, Z., Fan, D. & Triantafyllou, M.S. 2021 Illuminating the complex role of the added mass during vortex induced vibration. Phys. Fluids 33 (8), 085120.Google Scholar
Williamson, C.H.K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455.CrossRefGoogle Scholar
Xu, W., Ji, C., Sun, H., Ding, W. & Bernitsas, M.M. 2019 Flow-induced vibration of two elastically mounted tandem cylinders in cross-flow at subcritical Reynolds numbers. Ocean Engng 173, 375–387.CrossRefGoogle Scholar
Zdravkovich, M.M. 1977 Review of flow interference between two circular cylinders in various arrangements. J. Fluids Eng. 99 (4), 618–633.CrossRefGoogle Scholar
Zdravkovich, M.M. 1985 Flow induced oscillations of two interfering circular cylinders. J. Sound Vib. 101 (4), 511–521.CrossRefGoogle Scholar
Zhao, M. 2013 Flow induced vibration of two rigidly coupled circular cylinders in tandem and side-by-side arrangements at a low Reynolds number of 150. Phys. Fluids 25 (12), 123601.Google Scholar
Zhou, Y. & Alam, M.M. 2016 Wake of two interacting circular cylinders: a review. Intl J. Heat Fluid Flow 62, 510–537.CrossRefGoogle Scholar
Zhu, H., Zhao, Y., Qiu, T., Lin, W., Du, X. & Dong, H. 2023 Vortex-induced vibrations of two tandem rigidly coupled circular cylinders with streamwise, transverse, and rotational degrees of freedom. Phys. Fluids 35 (2), 023606.Google Scholar