Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-29T04:40:00.798Z Has data issue: false hasContentIssue false
  • English
  • Français

Macroscopic and kinetic modelling of rarefied polyatomic gases

Published online by Cambridge University Press:  11 October 2016

Behnam Rahimi  and
Henning Struchtrup
Behnam Rahimi*
Affiliation:
Department of Mechanical Engineering, University of Victoria, Victoria, British Columbia V8W 2Y2, Canada
Henning Struchtrup
Affiliation:
Department of Mechanical Engineering, University of Victoria, Victoria, British Columbia V8W 2Y2, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

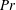A kinetic model and corresponding high-order macroscopic model for the accurate description of rarefied polyatomic gas flows are introduced. The different energy exchange processes are accounted for with a two term collision model. The proposed kinetic model, which is an extension of the S-model, predicts correct relaxation of higher moments and delivers the accurate Prandtl ($Pr$) number. Also, the model has a proven linear H-theorem. The order of magnitude method is applied to the primary moment equations to acquire the optimized moment definitions and the final scaled set of Grad’s 36 moment equations for polyatomic gases. At the first order, a modification of the Navier–Stokes–Fourier (NSF) equations is obtained. At third order of accuracy, a set of 19 regularized partial differential equations (R19) is obtained. Furthermore, the terms associated with the internal degrees of freedom yield various intermediate orders of accuracy, a total of 13 different orders. Thereafter, boundary conditions for the proposed macroscopic model are introduced. The unsteady heat conduction of a gas at rest is studied numerically and analytically as an example of a boundary value problem. The results for different gases are given and effects of Knudsen numbers, degrees of freedom, accommodation coefficients and temperature-dependent properties are investigated. For some cases, the higher-order effects are very dominant and the widely used first-order set of the NSF equations fails to accurately capture the gas behaviour and should be replaced by the proposed higher-order set of equations.

JFM classification

Mathematical Foundations: Mathematical Foundations Micro-/Nano-fluid dynamics: Micro-/Nano-fluid dynamics Rarefied Gas Flow: Rarefied Gas Flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 806 , 10 November 2016 , pp. 437 - 505
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andries, P., Tallec, P. L., Perlat, J.-P. & Perthame, B. 2000 The Gaussian-BGK model of Boltzmann equation with small Prandtl number. Eur. J. Mech. (B/Fluids) 19 (6), 813–830.Google Scholar
Arima, T., Taniguchi, S., Ruggeri, T. & Sugiyama, M. 2012 Extended thermodynamics of dense gases. Contin. Mech. Thermodyn. 24 (4–6), 271–292.Google Scholar
Boltzmann, L. 1872 Weitere studien über das wärmegleichgewicht unter gasmolekülen. Sitz.ber. Akad. Wiss. Wien 66 (2), 275–370.Google Scholar
Borgnakke, C. & Sonntag, R. E. 2009 Fundamentals of Thermodynamics. Wiley.Google Scholar
Bourgat, J.-F., Desvillettes, L., Le Tallec, P. & Perthame, B. 1994 Microreversible collisions for polyatomic gases and Boltzmann’s theorem. Eur. J. Mech. (B/Fluids) 13 (2), 237–254.Google Scholar
Brull, S. & Schneider, J. 2009 On the ellipsoidal statistical model for polyatomic gases. Contin. Mech. Thermodyn. 20 (8), 489–508.Google Scholar
Cai, Z. & Li, R. 2014 The NRxx method for polyatomic gases. J. Comput. Phys. 267, 63–91.Google Scholar
Chikhaoui, A., Dudon, J. P., Genieys, S., Kustova, E. V. & Nagnibeda, E. A. 2000 Multitemperature kinetic model for heat transfer in reacting gas mixture flows. Phys. Fluids 12 (1), 220–232.Google Scholar
Chikhaoui, A., Dudon, J. P., Kustova, E. V. & Nagnibeda, E. A. 1997 Transport properties in reacting mixture of polyatomic gases. Physica A 247 (1), 526–552.Google Scholar
Cramer, M. S. 2012 Numerical estimates for the bulk viscosity of ideal gases. Phys. Fluids 24 (6), 066102.Google Scholar
Gallis, M. A., Torczynski, J. R. & Rader, D. J. 2007 A computational investigation of noncontinuum gas-phase heat transfer between a heated microbeam and the adjacent ambient substrate. Sensors Actuators A 134 (1), 57–68.Google Scholar
Gallis, M. A. & Torczynski, J. R. 2011 Investigation of the ellipsoidal-statistical Bhatnagar–Gross–Krook kinetic model applied to gas-phase transport of heat and tangential momentum between parallel walls. Phys. Fluids 23 (3), 030601.Google Scholar
Grad, H. 1949 On the kinetic theory of rarefied gases. Commun. Pure Appl. Math. 2 (4), 331–407.Google Scholar
Grad, H. 1958 Principles of the kinetic theory of gases. In Thermodynamik der Gase/Thermodynamics of Gases, pp. 205–294. Springer.Google Scholar
Gad-el Hak, M. 2001 The MEMS Handbook. CRC Press.Google Scholar
Holway, L. H. 1966 New statistical models for kinetic theory: methods of construction. Phys. Fluids 9 (9), 1658–1673.Google Scholar
Karniadakis, G. E., Beskok, A. & Aluru, N. 2006 Microflows and Nanoflows: Fundamentals and Simulation, vol. 29. Springer.Google Scholar
Kremer, G. M. 2010 An Introduction to the Boltzmann Equation and Transport Processes in Gases. Springer.Google Scholar
Kustova, E. V. & Nagnibeda, E. A. 1996 Strong nonequilibrium effects on specific heats and thermal conductivity of diatomic gas. Chem. Phys. 208 (3), 313–329.Google Scholar
Kustova, E. V. & Nagnibeda, E. A. 1998 Transport properties of a reacting gas mixture with strong vibrational and chemical nonequilibrium. Chem. Phys. 233 (1), 57–75.Google Scholar
Kustova, E. V., Nagnibeda, E. A. & Chauvin, A. H. 1999 State-to-state nonequilibrium reaction rates. Chem. Phys. 248 (2), 221–232.Google Scholar
Marques, W. 1999 Light scattering from extended kinetic models: polyatomic ideal gases. Physica A 264 (1), 40–51.Google Scholar
Maxwell, J. C. 1879 On stresses in rarified gases arising from inequalities of temperature. Phil. Trans. R. Soc. Lond. 170, 231–256.Google Scholar
Müller, I. & Ruggeri, T. 2013 Rational Extended Thermodynamics, vol. 37. Springer.Google Scholar
Nagnibeda, E. & Kustova, E. 2009 Non-Equilibrium Reacting Gas Flows: Kinetic Theory of Transport and Relaxation Processes. Springer.CrossRefGoogle Scholar
Poling, B. E., Prausnitz, J. M., O’connell, J. P. & others 2001 The Properties of Gases and Liquids, vol. 5. McGraw-Hill.Google Scholar
Rahimi, B. & Niazmand, H. 2014 Effects of high order slip/jump, thermal creep and variable thermo-physical properties on natural convection in microchannels with constant wall heat fluxes. Heat Transfer Engng 35 (18), 1528–1538.Google Scholar
Rahimi, B. & Struchtrup, H. 2014a Capturing non-equilibrium phenomena in rarefied polyatomic gases: a high-order macroscopic model. Phys. Fluids 26 (5), 052001.Google Scholar
Rahimi, B. & Struchtrup, H. 2014b Kinetic model and moment method for polyatomic gases. AIP Conf. Proc. 1628 (1), 618–625.Google Scholar
Rahimi, B. & Struchtrup, H. 2014c Refined Navier–Stokes–Fourier equations for rarefied polyatomic gases. In ASME 2014 12th International Conference on Nanochannels, Microchannels, and Minichannels Collocated with the ASME 2014 4th Joint US-European Fluids Engineering Division Summer Meeting, pp. V001T01A001–V001T01A001. American Society of Mechanical Engineers.Google Scholar
Rana, A., Torrilhon, M. & Struchtrup, H. 2013 A robust numerical method for the r13 equations of rarefied gas dynamics: application to lid driven cavity. J. Comput. Phys. 236, 169–186.Google Scholar
Reif, F. 2009 Fundamentals of Statistical and Thermal Physics. Waveland.Google Scholar
Ruggeri, T. & Sugiyama, M. 2015 Rational Extended Thermodynamics beyond the Monatomic Gas. Springer.Google Scholar
Rykov, V. A. 1975 A model kinetic equation for a gas with rotational degrees of freedom. Fluid Dyn. 10 (6), 959–966.Google Scholar
Shakhov, E. M. 1968 Generalization of the Krook kinetic relaxation equation. Fluid Dyn. 3 (5), 95–96.Google Scholar
Sharipov, F. 2003 Application of the Cercignani–Lampis scattering kernel to calculations of rarefied gas flows. II. Slip and jump coefficients. Eur. J. Mech. (B/Fluids) 22 (2), 133–143.Google Scholar
Singh, N. & Agrawal, A. 2014 The Burnett equations in cylindrical coordinates and their solution for flow in a microtube. J. Fluid Mech. 751, 121–141.Google Scholar
Sone, Y. 2012 Kinetic Theory and Fluid Dynamics. Springer.Google Scholar
Struchtrup, H. 2004 Stable transport equations for rarefied gases at high orders in the Knudsen number. Phys. Fluids 16 (11), 3921–3934.Google Scholar
Struchtrup, Henning 2005a Derivation of 13 moment equations for rarefied gas flow to second order accuracy for arbitrary interaction potentials. Multiscale Model. Simul. 3 (1), 221–243.Google Scholar
Struchtrup, H. 2005b Macroscopic Transport Equations for Rarefied Gas Flows. Springer.Google Scholar
Struchtrup, H. 2012 Unique moment set from the order of magnitude method. Kinet. Relat. Models 5, 417–440.Google Scholar
Struchtrup, H. & Torrilhon, M. 2013 Regularized 13 moment equations for hard sphere molecules: linear bulk equations. Phys. Fluids 25 (5), 052001.Google Scholar
Tantos, C., Valougeorgis, D. & Frezzotti, A. 2015 Conductive heat transfer in rarefied polyatomic gases confined between parallel plates via various kinetic models and the {DSMC} method. Intl J. Heat Mass Transfer 88, 636–651.Google Scholar
Tantos, C., Valougeorgis, D., Pannuzzo, M., Frezzotti, A. & Morini, G. L. 2014 Conductive heat transfer in a rarefied polyatomic gas confined between coaxial cylinders. Intl J. Heat Mass Transfer 79, 378–389.Google Scholar
Torrilhon, M., Au, J. D. & Struchtrup, H. 2003 Explicit fluxes and productions for large systems of the moment method based on extended thermodynamics. Contin. Mech. Thermodyn. 15 (1), 97–111.Google Scholar
Torrilhon, M. & Struchtrup, H. 2008 Boundary conditions for regularized 13-moment-equations for micro-channel-flows. J. Comput. Phys. 227 (3), 1982–2011.Google Scholar
Truesdell, C. & Muncaster, R. G. 1980 Fundamentals of Maxwell’s Kinetic Theory of a Simple Monatomic Gas. Academic.Google Scholar
Wu, L., White, C., Scanlon, T. J., Reese, J. M. & Zhang, Y. 2015 A kinetic model of the Boltzmann equation for non-vibrating polyatomic gases. J. Fluid Mech. 763, 24–50.Google Scholar