Article contents
Mach-number scaling of individual azimuthal modes of subsonic co-flowing jets
Published online by Cambridge University Press: 14 March 2016
Abstract
The Mach-number scaling of the individual azimuthal modes of jet mixing noise was studied for jets in flight conditions, i.e. with co-flow. The data were obtained via a series of direct numerical simulations (DNS), performed of fully turbulent jets with a target Reynolds number, based on nozzle diameter, of 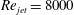 $Re_{jet}=8000$. The DNS included a pipe 25 diameters in length in order to ensure that the flow developed to a fully turbulent state before exiting into a laminar co-flow, and to account for all possible noise generation mechanisms. To allow for a detailed study of the jet mixing noise component of the combined pipe–jet configuration, acoustic liner boundary conditions on the inside of the pipe and a modification to the synthetic turbulent inlet boundary condition of the pipe were applied to minimize internal noise in the pipe. Despite these measures, the use of a phased-array source breakdown technique was essential in order to isolate the sources associated with jet noise mechanisms from additional noise sources that could be attributed to internal noise or unsteady flow past the nozzle lip, in particular for the axisymmetric mode. Decomposing the sound radiation from the pipe–jet configuration into its azimuthal Fourier modes, and accounting for the co-flow effects, it was found that at
$Re_{jet}=8000$. The DNS included a pipe 25 diameters in length in order to ensure that the flow developed to a fully turbulent state before exiting into a laminar co-flow, and to account for all possible noise generation mechanisms. To allow for a detailed study of the jet mixing noise component of the combined pipe–jet configuration, acoustic liner boundary conditions on the inside of the pipe and a modification to the synthetic turbulent inlet boundary condition of the pipe were applied to minimize internal noise in the pipe. Despite these measures, the use of a phased-array source breakdown technique was essential in order to isolate the sources associated with jet noise mechanisms from additional noise sources that could be attributed to internal noise or unsteady flow past the nozzle lip, in particular for the axisymmetric mode. Decomposing the sound radiation from the pipe–jet configuration into its azimuthal Fourier modes, and accounting for the co-flow effects, it was found that at 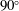 $90^{\circ }$ the individual azimuthal Fourier modes of far-field pressure for the jet mixing noise component exhibit the same
$90^{\circ }$ the individual azimuthal Fourier modes of far-field pressure for the jet mixing noise component exhibit the same 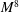 $M^{8}$ scaling with the centreline jet Mach number as that experimentally documented for the overall noise field. Applying the phased-array source breakdown code to the DNS data at smaller angles to the jet axis, an increase of the velocity exponent of the jet noise source was found, approaching 10 at
$M^{8}$ scaling with the centreline jet Mach number as that experimentally documented for the overall noise field. Applying the phased-array source breakdown code to the DNS data at smaller angles to the jet axis, an increase of the velocity exponent of the jet noise source was found, approaching 10 at 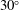 $30^{\circ }$. At this smaller angle the higher azimuthal modes again showed the same behaviour as the axisymmetric mode.
$30^{\circ }$. At this smaller angle the higher azimuthal modes again showed the same behaviour as the axisymmetric mode.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 12
- Cited by



