Hostname: page-component-f554764f5-68cz6 Total loading time: 0 Render date: 2025-04-20T06:50:48.142Z Has data issue: false hasContentIssue false
  • English
  • Français

Low-dimensional analysis and modelling of the flow over a forward-facing step

Published online by Cambridge University Press:  28 November 2024

B. Podvin Open the ORCID record for B. Podvin [Opens in a new window]  and
Y. Fraigneau
B. Podvin*
Affiliation:
EM2C, Centralesupélec, CNRS, Université Paris-Saclay, 91190 Gif/Yvette, France
Y. Fraigneau
Affiliation:
LISN, CNRS, Université Paris-Saclay, 91405 Orsay, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

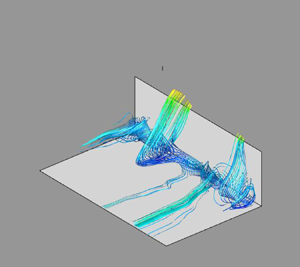
We consider the direct numerical simulation of the flow over a forward-facing step protruding in a turbulent boundary layer. Proper orthogonal decomposition (POD) is applied to the velocity field in different regions using Fourier modes in the spanwise direction. The upstream flow is characterized by a structure with a spanwise modulation of the order of the step height, the origin of which is consistent with a centrifugal instability. The structure is associated with ejections over the step of low-speed fluid from the upstream recirculation, and organized into streaks through the action of strong spanwise motions along the step face. The spanwise-averaged instantaneous momentum deficit created by the ejections is directly related to the maximal shear rate at the edge of the step, and is well correlated with the dynamics of the downstream recirculation. The most energetic patterns consist of three-dimensional motions with a large spanwise wavelength located in the shear layer developing at the edge of the step, as well as two-dimensional fluctuations downstream of the reattachment. A linear model based on the interaction of the mean flow with the dominant POD modes is able to recover the main frequencies of the fluctuations at these wavenumbers. Including the time variations of the ejections into the model yields temporal spectra that resemble qualitatively those computed from the simulation. The results suggest that the global dynamics of the flow are at least partly driven by linear mechanisms and depend on the characteristic structure identified in the upstream region close to the step.

JFM classification

Nonlinear Dynamical Systems: Low-dimensional models Boundary Layers: Boundary layer separation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1000 , 10 December 2024 , A69
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aubry, N., Holmes, P., Lumley, J.L. & Stone, E. 1988 The dynamics of coherent structures in the wall region of the wall boundary layer. J. Fluid Mech. 192, 115–173.CrossRefGoogle Scholar
Beam, R.M. & Warming, R.F. 1976 An implicit finite-difference algorithm for hyperbolic conservation-law form. J. Comput. Phys. 22, 87–110.CrossRefGoogle Scholar
Beaudoin, J.-F., Cadot, O., Aider, J.-L. & Wesfreid, J.E. 2004 Three-dimensional stationary flow over a backward-facing step. Eur. J. Mech. (B/Fluids) 23 (1), 147–155.CrossRefGoogle Scholar
Brès, G.A. & Colonius, T. 2008 Three-dimensional instabilities in compressible flow over open cavities. J. Fluid Mech. 599, 309–339.CrossRefGoogle Scholar
Buxton, O.R.H., de Kat, R. & Ganapathisubramani, B. 2013 The convection of large and intermediate scale fluctuations in a turbulent mixing layer. Phys. Fluids 25 (12), 125105.CrossRefGoogle Scholar
Camussi, R., Felli, M., Pereira, F., Aloisio, G. & Marco, A.D. 2008 Statistical properties of wall pressure fluctuations over a forward-facing step. Phys. Fluids 20 (7), 075113.CrossRefGoogle Scholar
Dagaut, J., Negretti, M.E., Balarac, G. & Brun, C. 2021 Linear to turbulent Görtler instability transition. Phys. Fluids 33 (1), 014102.CrossRefGoogle Scholar
Drazin, P.G. & Reid, W.H. 1982 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Erm, L.P. & Joubert, P.N. 1991 Low-Reynolds-number turbulent boundary layers. J. Fluid Mech. 230, 1–44.CrossRefGoogle Scholar
Fang, X. & Tachie, M.F. 2020 Spatio-temporal dynamics of flow separation induced by a forward-facing step submerged in a thick turbulent boundary layer. J. Fluid Mech. 892, A40.CrossRefGoogle Scholar
Fang, X., Tachie, M.F., Bergstrom, D.J., Yang, Z. & Wang, B.-C. 2021 Three-dimensional structural characteristics of flow separation induced by a forward-facing step in a turbulent channel flow. J. Fluid Mech. 919, A24.CrossRefGoogle Scholar
Farabee, T.M. & Casarella, M.J. 1986 Measurements of fluctuating wall pressure for separated/reattached boundary layer flows. ASME J. Vib. Acoust. Stress Reliab. 108 (108), 301–307.CrossRefGoogle Scholar
Faugaret, A., Duguet, Y., Fraigneau, Y. & Martin-Witkowski, L. 2022 A simple model for arbitrary pollution effects on rotating free-surface flows. J. Fluid Mech. 935, A2.CrossRefGoogle Scholar
Fraigneau, Y. 2024 SUNFLUIDH: a research software for the computational fluid dynamics. User's Guide (last release). Available at: https://sunfluidh.lisn.upsaclay.fr. LISN.Google Scholar
Goda, K. 1979 A multistep technique with implicit difference schemes for calculating two- or three-dimensional cavity flows. J. Comput. Phys. 30, 76–95.CrossRefGoogle Scholar
Graziani, A., Kerhervé, F., Martinuzzi, R.J. & Keirsbulck, L. 2018 Dynamics of the recirculating areas of a forward-facing step. Exp. Fluids 59, 154.CrossRefGoogle Scholar
Guermond, J.L., Minev, P.D. & Shen, J. 2006 An overview of projection methods for incompressible flows. Comput. Meth. Appl. Mech. Engng 195, 6011–6045.CrossRefGoogle Scholar
Hahn, C. 2008 Experimentelle Analyse und Reduktion aeroakustischer Schallquellen an einfachen Modellstrukturen. PhD thesis, Universitat Erlangen-Nurnberg.Google Scholar
Hammond, D.A. & Redekopp, L.G. 1998 Local and global instability properties of separation bubbles. Eur. J. Mech. (B/Fluids) 17 (2), 145–164.CrossRefGoogle Scholar
Harlow, F.H. & Welch, J.E. 1965 Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface. Phys. Fluids 8, 2182–2189.CrossRefGoogle Scholar
Hattori, H. & Nagano, Y. 2010 Investigation of turbulent boundary layer over forward-facing step via direct numerical simulation. Intl J. Heat Fluid Flow 31, 284–294.CrossRefGoogle Scholar
Ho, C.M. & Huerre, P. 1984 Perturbed free shear layers. Annu. Rev. Fluid Mech. 16, 365–422.CrossRefGoogle Scholar
Hoarau, C., Borée, J., Laumonier, J. & Gervais, Y. 2006 Analysis of the wall pressure trace downstream of a separated region using extended proper orthogonal decomposition. Phys. Fluids 18 (5), 055107.CrossRefGoogle Scholar
Holmes, P., Lumley, J.L. & Berkooz, G. 1996 Turbulence, Coherent Structures, Dynamical Systems and Symmetry. Cambridge University Press.CrossRefGoogle Scholar
Kiya, M. & Sasaki, K. 1983 Structure of a turbulent separation bubble. J. Fluid Mech. 137, 83–113.CrossRefGoogle Scholar
Kiya, M. & Sasaki, K. 1985 Structure of large-scale vortices and unsteady reverse flow in the reattaching zone of a turbulent separation bubble. J. Fluid Mech. 154, 463–491.CrossRefGoogle Scholar
Lanzerstorfer, D. & Kuhlmann, H.C. 2012 Three-dimensional instability of the flow over a forward facing step. J. Fluid Mech. 695, 390–404.CrossRefGoogle Scholar
Largeau, J.F. & Moriniere, V. 2007 Wall pressure fluctuations and topology in separated flows over a forward-facing step. Exp. Fluids 42 (1), 21–40.CrossRefGoogle Scholar
Larose, E., Kerhervé, F., Fraigneau, Y., Podvin, B., Morton, C. & Martinuzzi, R. 2024 Experimental and numerical investigation of oncoming flow conditions on the dynamics of flow over a forward-facing step. In Proceedings of the Thirteenth International Symposium on Turbulence and Shear Flow Phenomena (TSFP13), 25–28 June, Montréal, Canada.Google Scholar
Lumley, J.L. 1967 The structure of inhomogeneous turbulent flows. In Atmospheric Turbulence and Radio Wave Propagation (ed. A.M Iaglom & V.I Tatarski), pp. 221–227. Nauka.Google Scholar
Marino, L. & Luchini, P. 2009 Ajoint analysis of the flow over a forward-facing step. Theor. Comput. Fluid Dyn. 23, 37–54.CrossRefGoogle Scholar
Martinuzzi, R.J. & Tropea, C. 1993 The flow around surface-mounted, prismatic obstacles placed in a fully developed channel flow. Trans. ASME J. Fluids Engng 115, 85–92.CrossRefGoogle Scholar
McGuiness, M. 1978 Flow with a separation bubble-steady and unsteady aspects. PhD thesis, Cambridge University.Google Scholar
Moin, P. & Moser, R. 1989 Characteristic-eddy decomposition of turbulence in a channel. J. Fluid Mech. 200, 471–509.CrossRefGoogle Scholar
Moss, W.D. & Baker, S. 1980 Re-circulating flows associated with two-dimensional steps. Aeronaut. Q. 31 (3), 151–172.CrossRefGoogle Scholar
Noack, B., Papas, P. & Monkewitz, P. 2005 The need for a pressure-term representation in empirical Galerkin models of incompressible shear flows. J. Fluid Mech. 523, 339–365.CrossRefGoogle Scholar
Osth, J., Noack, B., Krajnoci, S., Borée, D. & Barros, J. 2014 On the need for a nonlinear subscale turbulence term in POD models as exemplified for a high-Reynolds-number flow over an Ahmed body. J. Fluid Mech. 474, 518–544.CrossRefGoogle Scholar
Pamies, M., Weiss, P.E., Garnier, E., Deck, S. & Sagaut, P. 2009 Generation of synthetic turbulent inflow data for large-eddy simulation of spatially evolving wall-bounded flows. Phys. Fluids 21, 045103.CrossRefGoogle Scholar
Peaceman, D.W. & Rachford, H.H. 1955 The numerical solution of parabolic and elliptic differential equations. Intl J. Ind. Maths 3, 28–41.Google Scholar
Pearson, D.S., Goulart, P.J. & Ganapathisubramani, B. 2013 Turbulent separation upstream of a forward facing step. J. Fluid Mech. 724, 284–304.CrossRefGoogle Scholar
Podvin, B., Pellerin, S., Fraigneau, Y., Bonnavion, G. & Cadot, O. 2021 Low-order modelling of the wake dynamics of an Ahmed body. J. Fluid Mech. 927, R6.CrossRefGoogle Scholar
Podvin, B. & Sergent, A. 2017 Precursor for wind reversal in a square Rayleigh–Bénard cell. Phys. Rev. E 05 (1), 013112.CrossRefGoogle Scholar
Saric, W.S. 1994 Görtler vortices. Annu. Rev. Fluid Mech. 26 (1), 379–409.CrossRefGoogle Scholar
Sherry, M., Jacono, D.L. & Sheridan, J. 2010 An experimental investigation of the recirculation zone formed downstream of a forward facing step. J. Wind Engng Ind. Aerodyn. 98, 888–894.CrossRefGoogle Scholar
Sipp, D. & Jacquin, L. 2000 A criterion of centrifugal instabilities in rotating systems. In Vortex Structure and Dynamics. Springer.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. Part I: coherent structures. Q. Appl. Maths 45 (3), 561–571.CrossRefGoogle Scholar
Spalart, P.R. 1988 Direct numerical simulation of a turbulent boundary layer up to $Re_{\theta }=1410$. J. Fluid Mech. 187, 61–98.CrossRefGoogle Scholar
Stuer, H. 1999 Investigation of separation over a forward-facing step. PhD thesis, ETH Zurich.Google Scholar
Stuer, H., Gyr, A. & Kinzelbach, W. 1999 Laminar separation on a forward facing step. Eur. J. Mech. (B/FLuids) 18 (4), 675–692.CrossRefGoogle Scholar
Tani, I. 1962 Production of longitudinal vortices in the boundary layer along a concave wall. J. Geophys. Res. 67, 3075–80.CrossRefGoogle Scholar
Tenaud, C., Podvin, B., Fraigneau, Y. & Daru, V. 2016 On wall pressure fluctuations and their coupling with vortex dynamics in a separated-reattached turbulent flow over a blunt flat plate. Intl J. Heat Fluid Flow 61, 730–748.CrossRefGoogle Scholar
Weiss, J., Mohammed-Taifour, A. & Schwaab, Q. 2015 Unsteady behavior of a pressure-induced turbulent separation bubble. AIAA J. 53 (9), 2634–2645.CrossRefGoogle Scholar
Wilhelm, D., Hartel, C. & Kleiser, L. 2003 Computational analysis of the two-dimensional–three-dimensional transition in forward facing step flow. J. Fluid Mech. 489, 1–27.CrossRefGoogle Scholar
Wills, J.A.B. 1964 On convection velocities in turbulent shear flows. J. Fluid Mech. 20 (3), 417–432.CrossRefGoogle Scholar