Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Khusnutdinova, Karima R.
and
Zhang, Xizheng
2016.
Nonlinear ring waves in a two-layer fluid.
Physica D: Nonlinear Phenomena,
Vol. 333,
Issue. ,
p.
208.
Khusnutdinova, K. R.
Stepanyants, Y. A.
and
Tranter, M. R.
2018.
Soliton solutions to the fifth-order Korteweg–de Vries equation and their applications to surface and internal water waves.
Physics of Fluids,
Vol. 30,
Issue. 2,
Ali, Mohammed
Alquran, Marwan
Jaradat, Imad
and
Baleanu, Dumitru
2019.
Stationary wave solutions for new developed two-waves’ fifth-order Korteweg–de Vries equation.
Advances in Difference Equations,
Vol. 2019,
Issue. 1,
Akselsen, Andreas H.
and
Ellingsen, Simen Å.
2019.
Weakly nonlinear transient waves on a shear current: ring waves and skewed Langmuir rolls.
Journal of Fluid Mechanics,
Vol. 863,
Issue. ,
p.
114.
Grimshaw, Roger
2019.
Initial conditions for the cylindrical Korteweg‐de Vries equation.
Studies in Applied Mathematics,
Vol. 143,
Issue. 2,
p.
176.
Smeltzer, Benjamin K.
Æsøy, Eirik
and
Ellingsen, Simen Å.
2019.
Observation of surface wave patterns modified by sub-surface shear currents.
Journal of Fluid Mechanics,
Vol. 873,
Issue. ,
p.
508.
Khusnutdinova, Karima
2020.
Long internal ring waves in a two-layer fluid with an upper-layer current.
Russian Journal of Earth Sciences,
Vol. 20,
Issue. 4,
p.
1.
la Forgia, Giovanni
Ottolenghi, Luisa
Adduce, Claudia
and
Falcini, Federico
2020.
Intrusions and solitons: Propagation and collision dynamics.
Physics of Fluids,
Vol. 32,
Issue. 7,
Bulatov, V. V.
and
Vladimirov, I. Yu.
2021.
Amplitude-phase Structure of Internal Gravity Waves Fields in Ocean with Shear Flows.
Izvestiya, Atmospheric and Oceanic Physics,
Vol. 57,
Issue. 6,
p.
680.
Hooper, Curtis
Khusnutdinova, Karima
and
Grimshaw, Roger
2021.
Wavefronts and modal structure of long surface and internal ring waves on a parallel shear current.
Journal of Fluid Mechanics,
Vol. 927,
Issue. ,
Wang, Aimin
Zong, Zhi
Zou, Li
Pei, Yuguo
and
Hu, Yingjie
2021.
Experimental observation of O-solitary waves in shallow water.
Physics of Fluids,
Vol. 33,
Issue. 12,
Hu, Wencheng
Ren, Jingli
and
Stepanyants, Yury
2023.
Solitary Waves and Their Interactions in the Cylindrical Korteweg–De Vries Equation.
Symmetry,
Vol. 15,
Issue. 2,
p.
413.
Tseluiko, D
Alharthi, N S
Barros, R
and
Khusnutdinova, K R
2023.
Internal ring waves in a three-layer fluid on a current with a constant vertical shear.
Nonlinearity,
Vol. 36,
Issue. 6,
p.
3431.
Hu, Wencheng
Zhang, Zhao
Guo, Qi
and
Stepanyants, Yury
2024.
Solitons and lumps in the cylindrical Kadomtsev–Petviashvili equation. I. Axisymmetric solitons and their stability.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 34,
Issue. 1,
Sidorovas, Nerijus
Tseluiko, Dmitri
Choi, Wooyoung
and
Khusnutdinova, Karima
2024.
Nonlinear concentric water waves of moderate amplitude.
Wave Motion,
Vol. 128,
Issue. ,
p.
103295.
Ostrovsky, L.
Pelinovsky, E.
Shrira, V.
and
Stepanyants, Y.
2024.
Localized wave structures: Solitons and beyond.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 34,
Issue. 6,
Kairzhan, Adilbek
Kennedy, Christopher
and
Sulem, Catherine
2024.
Interaction Between Long Internal Waves and Free Surface Waves in Deep Water.
Water Waves,
Vol. 6,
Issue. 3,
p.
477.
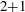 $2+1$-dimensional cylindrical Korteweg–de Vries-type equation for the amplitudes of the waves. The general theory is applied to the case of the waves in a two-layer fluid with a piecewise-constant current, with an emphasis on the effect of the shear flow on the geometry of the wavefronts. The distortion of the wavefronts is described by the singular solution (envelope of the general solution) of the nonlinear first-order differential equation, constituting generalisation of the dispersion relation in this curvilinear geometry. There exists a striking difference in the shapes of the wavefronts of surface and interfacial waves propagating over the same shear flow.
$2+1$-dimensional cylindrical Korteweg–de Vries-type equation for the amplitudes of the waves. The general theory is applied to the case of the waves in a two-layer fluid with a piecewise-constant current, with an emphasis on the effect of the shear flow on the geometry of the wavefronts. The distortion of the wavefronts is described by the singular solution (envelope of the general solution) of the nonlinear first-order differential equation, constituting generalisation of the dispersion relation in this curvilinear geometry. There exists a striking difference in the shapes of the wavefronts of surface and interfacial waves propagating over the same shear flow.


