Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-28T06:44:24.391Z Has data issue: false hasContentIssue false
  • English
  • Français

Logarithmic temperature profiles of turbulent Rayleigh–Bénard convection in the classical and ultimate state for a Prandtl number of 0.8

Published online by Cambridge University Press:  09 October 2014

Guenter Ahlers ,
Eberhard Bodenschatz  and
Xiaozhou He
Guenter Ahlers*
Affiliation:
Department of Physics, University of California, Santa Barbara, CA 93106, USA Max Planck Institute for Dynamics and Self-Organization (MPIDS), 37077 Göttingen, Germany
Eberhard Bodenschatz
Affiliation:
Max Planck Institute for Dynamics and Self-Organization (MPIDS), 37077 Göttingen, Germany Institute for Nonlinear Dynamics, University of Göttingen, 37077 Göttingen, Germany Laboratory of Atomic and Solid-State Physics, and Sibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, NY 14853, USA
Xiaozhou He
Affiliation:
Max Planck Institute for Dynamics and Self-Organization (MPIDS), 37077 Göttingen, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We report on experimental determinations of the temperature field in the interior (bulk) of turbulent Rayleigh–Bénard convection for a cylindrical sample with an aspect ratio (diameter 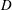$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}D$ over height 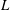$L$) equal to 0.50, in both the classical and the ultimate state. The measurements are for Rayleigh numbers 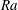$\mathit{Ra}$ from 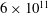$6\times 10^{11}$ to 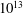$10^{13}$ in the classical and 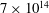$7\times 10^{14}$ to 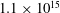$1.1\times 10^{15}$ (our maximum accessible 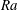$\mathit{Ra}$) in the ultimate state. The Prandtl number was close to 0.8. Although to lowest order the bulk is often assumed to be isothermal in the time average, we found a ‘logarithmic layer’ (as reported briefly by Ahlers et al., Phys. Rev. Lett., vol. 109, 2012, 114501) in which the reduced temperature 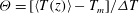$\varTheta = [\langle T(z) \rangle - T_m]/\Delta T$ (with 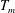$T_m$ the mean temperature, 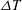$\Delta T$ the applied temperature difference and 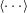$\langle {\cdots } \rangle $ a time average) varies as 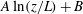$A \ln (z/L) + B$ or 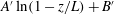$A^{\prime } \ln (1-z/L) + B^{\prime }$ with the distance $z$ from the bottom plate of the sample. In the classical state, the amplitudes 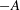$-A$ and 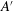$A^{\prime }$ are equal within our resolution, while in the ultimate state there is a small difference, with 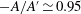$-A/A^{\prime } \simeq 0.95$. For the classical state, the width of the log layer is approximately 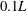$0.1L$, the same near the top and the bottom plate as expected for a system with reflection symmetry about its horizontal midplane. For the ultimate state, the log-layer width is larger, extending through most of the sample, and slightly asymmetric about the midplane. Both amplitudes 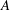$A$ and 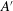$A^{\prime }$ vary with radial position $r$, and this variation can be described well by 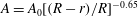$A = A_0 [(R - r)/R]^{-0.65}$, where 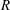$R$ is the radius of the sample. In the classical state, these results are in good agreement with direct numerical simulations (DNS) for 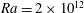$\mathit{Ra} = 2\times 10^{12}$; in the ultimate state there are as yet no DNS. The amplitudes $-A$ and 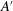$A^{\prime }$ varied as 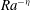${\mathit{Ra}}^{-\eta }$, with 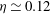$\eta \simeq 0.12$ in the classical and 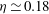$\eta \simeq 0.18$ in the ultimate state. A close analogy between the temperature field in the classical state and the ‘law of the wall’ for the time-averaged downstream velocity in shear flow is discussed. 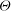A two-sublayer mean-field model of the temperature profile in the classical state was analysed and yielded a logarithmic $z$ dependence of $\varTheta $. The 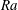$\mathit{Ra}$ dependence of the amplitude 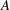$A$ given by the model corresponds to an exponent 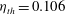$\eta _{th} = 0.106$, in good agreement with the experiment. In the ultimate state the experimental result 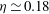$\eta \simeq 0.18$ differs from the prediction 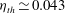$\eta _{th} \simeq 0.043$ by Grossmann & Lohse (Phys. Fluids, vol. 24, 2012, 125103).

JFM classification

Convection: Convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 758 , 10 November 2014 , pp. 436 - 467
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

The authors belong to the International Collaboration for Turbulence Research.

References

Ahlers, G. 2009 Turbulent convection. Physics 2, 74.CrossRefGoogle Scholar
Ahlers, G., Bodenschatz, E., Funfschilling, D., Grossmann, S., He, X., Lohse, D., Stevens, R. & Verzicco, R. 2012a Logarithmic temperature profiles in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 109, 114501.CrossRefGoogle ScholarPubMed
Ahlers, G., Brown, E., Fontenele Araujo, F., Funfschilling, D., Grossmann, S. & Lohse, D. 2006 Non-Oberbeck–Boussinesq effects in strongly turbulent Rayleigh–Bénard convection. J. Fluid Mech. 569, 409–445.CrossRefGoogle Scholar
Ahlers, G., Calzavarini, E., Fontenele Araujo, F., Funfschilling, D., Grossmann, S., Lohse, D. & Sugiyama, K. 2008 Non-Oberbeck–Boussinesq effects in turbulent thermal convection in ethane close to the critical point. Phys. Rev. E 77, 046302.CrossRefGoogle Scholar
Ahlers, G., Fontenele Araujo, F., Funfschilling, D., Grossmann, S. & Lohse, D. 2007 Non-Oberbeck–Boussinesq effects in gaseous Rayleigh–Bénard convection. Phys. Rev. Lett. 98, 054501.CrossRefGoogle ScholarPubMed
Ahlers, G., Funfschilling, D. & Bodenschatz, E. 2009a Transitions in heat transport by turbulent convection for $Pr = 0.8$ and $10^{11} \leq Ra \leq 10^{15}$ . New J. Phys. 11, 123001.Google Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009b Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–538.Google Scholar
Ahlers, G., He, X., Funfschilling, D. & Bodenschatz, E. 2012b Heat transport by turbulent Rayleigh–Bénard convection for $Pr \simeq 0.8$ and $3\times 10^{12} \lesssim Ra \lesssim 10^{15}$ : aspect ratio $\gamma = 0.50$ . New J. Phys. 14, 103012.Google Scholar
Bailon-Cuba, J., Emran, M. S. & Schumacher, J. 2010 Aspect ratio dependence of heat transfer and large-scale flow in turbulent convection. J. Fluid Mech. 655, 152–173.CrossRefGoogle Scholar
Boussinesq, J. 1903 Theorie Analytique de la Chaleur, vol. 2. Gauthier-Villars.Google Scholar
Brown, E. & Ahlers, G. 2007 Temperature gradients, and search for non-Boussinesq effects, in the interior of turbulent Rayleigh–Bénard convection. Europhys. Lett. 80, 14001.CrossRefGoogle Scholar
Chavanne, X., Chillà, F., Castaing, B., Hébral, B., Chabaud, B. & Chaussy, J. 1997 Observation of the ultimate regime in Rayleigh–Bénard convection. Phys. Rev. Lett. 79, 3648–3651.CrossRefGoogle Scholar
Chavanne, X., Chillà, F., Chabaud, B., Castaing, B. & Hébral, B. 2001 Turbulent Rayleigh–Bénard convection in gaseous and liquid He. Phys. Fluids 13, 1300–1320.CrossRefGoogle Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 58.CrossRefGoogle ScholarPubMed
Churchill, S. W. 2002 A reinterpretation of the turbulent Prandtl number. Ind. Engng Chem. Res. 41, 6393–6401.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying view. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl number. Phys. Rev. Lett. 86, 3316–3319.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2002 Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection. Phys. Rev. E 66, 016305.CrossRefGoogle ScholarPubMed
Grossmann, S. & Lohse, D. 2011 Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 23, 045108.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2012 Logarithmic temperature profiles in the ultimate regime of thermal convection. Phys. Fluids 24, 125103.CrossRefGoogle Scholar
He, X., Funfschilling, D., Bodenschatz, E. & Ahlers, G. 2012a Heat transport by turbulent Rayleigh–Bénard convection for $Pr\simeq 0.8$ and $4\times 10^{11} \lesssim {Ra} \lesssim 2\times 10^{14}$ : ultimate-state transition for aspect ratio $\gamma = 1.00$ . New J. Phys. 14, 063030.Google Scholar
He, X., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2012b Transition to the ultimate state of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108, 024502.CrossRefGoogle Scholar
He, X., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2013 Comment on ‘Effect of boundary layers asymmetry on heat transfer efficiency in turbulent Rayleigh–Bénard convection at very high Rayleigh numbers’ by Urban et al. Phys. Rev. Lett. 110, 199401.CrossRefGoogle Scholar
He, X., van Gils, D., Bodenschatz, E. & Ahlers, G. 2014 Logarithmic spatial variations and universal $f^{-1}$ power spectra of temperature fluctuations in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 112, 174501.Google ScholarPubMed
Hogg, J. & Ahlers, G. 2013 Reynolds-number measurements for low-Prandtl-number turbulent convection of large aspect-ratio samples. J. Fluid Mech. 725, 664–680.CrossRefGoogle Scholar
Jischa, M. & Rieke, H. B. 1979 About the prediction of turbulent Prandtl and Schmidt numbers from modeled transport equations. Intl J. Heat Mass Transfer 22, 1547–1555.CrossRefGoogle Scholar
Kadanoff, L. P. 2001 Turbulent heat flow: structures and scaling. Phys. Today 54 (8), 34–39.CrossRefGoogle Scholar
Kader, B. A. 1981 Temperature and concentration profiles in fully turbulent boundary layers. Intl J. Heat Mass Transfer 24, 1541–1544.CrossRefGoogle Scholar
Kader, B. A. & Yaglom, A. M. 1972 Heat and mass transfer laws for fully turbulent wall flows. Intl J. Heat Mass Transfer 15, 2329–2351.CrossRefGoogle Scholar
von Kármán, T. 1930 Mechanische ähnlichkeit und Turbulenz. Nachr. Ges. Wiss. Göttingen, Math.-Phys. Kl. 58–76, 322–336.Google Scholar
Kraichnan, R. H. 1962 Turbulent thermal convection at arbritrary Prandtl number. Phys. Fluids 5, 1374–1389.CrossRefGoogle Scholar
Landau, L. D. & Lifshitz, E. M. 1963 Fluid Mechanics (3rd impression). Pergamon Press.Google Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.CrossRefGoogle Scholar
Lui, S. L. & Xia, K.-Q. 1998 Spatial structure of the thermal boundary layer in turbulent convection. Phys. Rev. E 57, 5494–5503.CrossRefGoogle Scholar
Malkus, M. V. R. 1954 The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. A 225, 196–212.Google Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010 Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22, 065103.CrossRefGoogle Scholar
Niemela, J. J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. 2000 Turbulent convection at very high Rayleigh numbers. Nature 404, 837–840.CrossRefGoogle ScholarPubMed
Oberbeck, A. 1879 Über die Wärmeleitung der Flüssigkeiten bei Berücksichtigung der Strömungen infolge von Temperaturdifferenzen. Ann. Phys. Chem. 7, 271–292.CrossRefGoogle Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.CrossRefGoogle Scholar
Perry, A. E., Henbest, S. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.CrossRefGoogle Scholar
van der Poel, E. P., Mónico, R. O., Grossmann, S. & Lohse, D. 2013 Logarithmic mean temperature profiles in Rayleigh–Bénard convection simulations. In Proceedings of the 14th European Turbulence Conference, Lyon, France.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Prandtl, L. 1925 Bericht über Untersuchungen zur ausgebildeten Turbulenz. Z. Angew. Math. Mech. 5, 136–139.CrossRefGoogle Scholar
Prandtl, L. 1932 Zur turbulenten Strömung in Rohren und längs Platten. Ergeb. Aerodyn. Versuch. Göttingen IV, 18.Google Scholar
Priestley, C. H. B. 1954 Convection from a large horizontal surface. Aust. J. Phys. 7, 176–201.CrossRefGoogle Scholar
Priestley, C. H. B. 1959 Turbulent Transfer in the Lower Atmosphere. University of Chicago Press.Google Scholar
du Puits, R., Resagk, C. & Thess, A. 2009 Structure of viscous boundary layers in turbulent Rayleigh–Bénard convection. Phys. Rev. E 80, 036318.CrossRefGoogle ScholarPubMed
Qiu, X. L. & Tong, P. 2001 Large scale velocity structures in turbulent thermal convection. Phys. Rev. E 64, 036304.CrossRefGoogle ScholarPubMed
Reichardt, H. 1951 Die grundlagen des turbulent Warmeuberganges. Arch. Gesamte Warmetechnik 2, 129–142.Google Scholar
Roche, P.-E., Gauthier, F., Kaiser, R. & Salort, J. 2010 On the triggering of the ultimate regime of convection. New J. Phys. 12, 085014.CrossRefGoogle Scholar
Rosenberg, B. J., Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Turbulence spectra in smooth- and rough-wall pipe flow at extreme Reynolds numbers. J. Fluid Mech. 731, 46–63.CrossRefGoogle Scholar
She, Z.-S., Chen, X., Chen, J., Zou, H.-Y., Bao, Y. & Hussain, F.2014 Prediction of temperature distribution in turbulent Rayleigh–Bénard convection. arXiv:1401.2138v1.Google Scholar
Shishkina, O., Stevens, R., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12, 075022.CrossRefGoogle Scholar
Shishkina, O. & Thess, A. 2009 Mean temperature profiles in turbulent Rayleigh–Bénard convection of water. J. Fluid Mech. 633, 449–460.CrossRefGoogle Scholar
Shishkina, O., Wagner, S. & Horn, S. 2014 Influence of the angle between the wind and the isothermal surfaces on the boundary layer structures in turbulent thermal convection. Phys. Rev. E 89, 033014.CrossRefGoogle ScholarPubMed
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.CrossRefGoogle Scholar
Spiegel, E. A. 1971 Convection in stars. Annu. Rev. Astron. Astrophys. 9, 323–352.CrossRefGoogle Scholar
Stevens, R. J. A. M., Lohse, D. & Verzicco, R. 2011 Prandtl and Rayleigh number dependence of heat transport in high Rayleigh number thermal convection. J. Fluid Mech. 688, 31–43.CrossRefGoogle Scholar
Stevens, R. J. A. M., van der Poel, E. P., Grossmann, S. & Lohse, D. 2013 The unifying theory of scaling in thermal convection: the updated prefactors. J. Fluid Mech. 730, 295–308.CrossRefGoogle Scholar
Stevens, R. J. A. M., Zhou, Q., Grossmann, S., Verzicco, R., Xia, K.-Q. & Lohse, D. 2012 Thermal boundary layer profiles in turbulent Rayleigh–Bénard convection in a cylindrical sample. Phys. Rev. E 85, 027301.CrossRefGoogle Scholar
Tilgner, A., Belmonte, A. & Libchaber, A. 1993 Temperature and velocity profiles of turbulence convection in water. Phys. Rev. E 47, R2253–R2256.CrossRefGoogle ScholarPubMed
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Urban, P., Hanzelka, P., Kralik, T., Musilova, V., Srnka, A. & Skrbek, L. 2012 Effect of boundary layers asymmetry on heat transfer efficiency in turbulent Rayleigh–Bénard convection at very high Rayleigh numbers. Phys. Rev. Lett. 109, 154301.Google ScholarPubMed
Wei, P. & Ahlers, G. 2014 Logarithmic temperature profiles in the bulk of turbulent Rayleigh–Bénard convection for a Prandtl number of 12.3. J. Fluid Mech. doi:10.1017/jfm.2014.560.CrossRefGoogle Scholar
Wei, T. & Wilmarth, W. 1989 Reynolds-number effects on the structure of turbulent flows. J. Fluid Mech. 204, 57–95.CrossRefGoogle Scholar
Wu, X. Z.1991 Along a road to developed turbulence: free thermal convection in low temperature He gas. PhD thesis, University of Chicago, IL. [The data of Wu were re-evaluated on the basis of new fluid properties by Niemela et al. (2001, private communication)].Google Scholar
Wu, X. Z. & Libchaber, A. 1991 Non-Boussinesq effects in free thermal convection. Phys. Rev. A 43, 2833–2839.CrossRefGoogle ScholarPubMed
Yaglom, A. M. 1979 Similarity laws for constant-pressure and pressure-gradient turbulent wall flows. Annu. Rev. Fluid Mech. 11, 505–540.CrossRefGoogle Scholar
Yu, B., Ozoe, H. & Churchill, S. W. 2001 The characteristics of fully developed turbulent convection in a round tube. Chem. Engng Sci. 56, 1781–1800.CrossRefGoogle Scholar
Zhang, J., Childress, S. & Libchaber, A. 1997 Non-Boussinesq effect: thermal convection with broken symmetry. Phys. Fluids 9, 1034–1042.CrossRefGoogle Scholar
Zhou, Q., Sugiyama, K., Stevens, R., Grossmann, S., Lohse, D. & Xia, K.-Q. 2010 Prandtl–Blasius temperature and velocity boundary-layer profiles in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 664, 297–312.CrossRefGoogle Scholar
Zhou, Q. & Xia, K.-Q. 2010 Measured instantaneous viscous boundary layer in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 104, 104301.CrossRefGoogle ScholarPubMed
Zhou, Q. & Xia, K.-Q. 2013 Thermal boundary layer structure in turbulent Rayleigh–Bénard convection in a rectangular cell. J. Fluid Mech. 721, 199–224.CrossRefGoogle Scholar