Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T13:55:37.689Z Has data issue: false hasContentIssue false
  • English
  • Français

Lock-in regions of laminar flows over a streamwise oscillating circular cylinder

Published online by Cambridge University Press:  06 November 2018

Ki-Ha Kim  and
Jung-Il Choi Open the ORCID record for Jung-Il Choi [Opens in a new window]
Ki-Ha Kim
Affiliation:
Department of Computational Science and Engineering, Yonsei University, Seoul 03722, Republic of Korea
Jung-Il Choi*
Affiliation:
Department of Computational Science and Engineering, Yonsei University, Seoul 03722, Republic of Korea
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

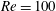In this paper, flow over a streamwise oscillating circular cylinder is numerically simulated to examine the effects of the driving amplitude and frequency on the distribution of the lock-in regions in laminar flows. At $Re=100$, lock-in is categorized according to the spectral features of the lift coefficient as two different lock-in phenomena: harmonic and subharmonic lock-in. These lock-in phenomena are represented as maps on the driving amplitude–frequency plane, which have subharmonic lock-in regions and two harmonic lock-in regions. The frequency range of the subharmonic region is shifted to lower frequencies with increasing amplitude, and the lower boundary of this subharmonic region is successfully predicted. A symmetric harmonic region with a symmetric vortex pattern is observed in a certain velocity range for a moving cylinder. Aerodynamic features induced by different flow patterns in each region are presented on the driving amplitude–frequency plane. The lock-in region and aerodynamic features at 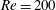$Re=200$ and 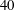$40$ are compared with the results for 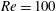$Re=100$. A subharmonic region and two harmonic regions are observed at 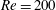$Re=200$, and these show the same features as for 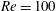$Re=100$ at a low driving amplitude. Lock-in at 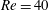$Re=40$ also shows one subharmonic region and two harmonic regions. However, compared with the 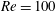$Re=100$ case, the symmetric harmonic lock-in is dominant. The features of aerodynamic force at 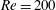$Re=200$ and 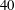$40$ are represented on a force map, which shows similar characteristics in corresponding regions for the 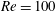$Re=100$ case.

JFM classification

Vortex Flows: Vortex shedding Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 858 , 10 January 2019 , pp. 315 - 351
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Al-Mdallal, Q. M.2004 Analysis and computation of the cross-flow past an oscillating cylinder with two degrees of freedom. PhD thesis, Memorial University of Newfoundland.Google Scholar
Al-Mdallal, Q. M., Lawrence, K. P. & Kocabiyik, S. 2007 Forced streamwise oscillations of a circular cylinder: locked-on modes and resulting fluid forces. J. Fluids Struct. 23 (5), 681–701.Google Scholar
Anagnostopoulos, P. 2000 Numerical study of the flow past a cylinder excited transversely to the incident stream. Part 1: lock-in zone, hydrodynamic forces and wake geometry. J. Fluids Struct. 14 (6), 819–851.Google Scholar
Barbi, C., Favier, D. P., Maresca, C. A. & Telionis, D. P. 1986 Vortex shedding and lock-on of a circular cylinder in oscillatory flow. J. Fluid Mech. 170, 527–544.Google Scholar
Bearman, P. W. 2011 Circular cylinder wakes and vortex-induced vibrations. J. Fluids Struct. 27 (5), 648–658.Google Scholar
Bishop, R. E. D. & Hassan, A. Y. 1964 The lift and drag forces on a circular cylinder in a flowing fluid. Proc. R. Soc. Lond. A 277 (1368), 32–50.Google Scholar
Blackburn, H. M & Henderson, R. D 1999 A study of two-dimensional flow past an oscillating cylinder. J. Fluid Mech. 385, 255–286.Google Scholar
Braza, M., Chassaing, P. H. H. M. & Minh, H. H. 1986 Numerical study and physical analysis of the pressure and velocity fields in the near wake of a circular cylinder. J. Fluid Mech. 165, 79–130.Google Scholar
Cetiner, O. & Rockwell, D. 2001 Streamwise oscillations of a cylinder in a steady current. Part 1. Locked-on states of vortex formation and loading. J. Fluid Mech. 427, 1–28.Google Scholar
Dahl, J. M., Hover, F. S., Triantafyllou, M. S. & Oakley, O. H. 2010 Dual resonance in vortex-induced vibrations at subcritical and supercritical Reynolds numbers. J. Fluid Mech. 643, 395–424.Google Scholar
Dütsch, H., Durst, F., Becker, S. & Lienhart, H. 1998 Low-Reynolds-number flow around an oscillating circular cylinder at low Keulegan–Carpenter numbers. J. Fluid Mech. 360, 249–271.Google Scholar
Feng, L. H. & Wang, J. J. 2010 Circular cylinder vortex-synchronization control with a synthetic jet positioned at the rear stagnation point. J. Fluid Mech. 662, 232–259.Google Scholar
Fey, U., König, M. & Eckelmann, H. 1998 A new Strouhal–Reynolds-number relationship for the circular cylinder in the range 47 < Re < 2 × 105 . Phys. Fluids 10 (7), 1547–1549.Google Scholar
Fornberg, B. 1980 A numerical study of steady viscous flow past a circular cylinder. J. Fluid Mech. 98 (04), 819–855.Google Scholar
Griffin, O. M. & Ramberg, S. E. 1976 Vortex shedding from a cylinder vibrating in line with an incident uniform flow. J. Fluid Mech. 75 (02), 257–271.Google Scholar
Hall, M. S. & Griffin, O. M. 1993 Vortex shedding and lock-on in a perturbed flow. Trans. ASME J. Fluids Engng 115, 283–283.Google Scholar
Kaiktsis, L., Triantafyllou, G. S. & Özbas, M. 2007 Excitation, inertia, and drag forces on a cylinder vibrating transversely to a steady flow. J. Fluids Struct. 23 (1), 1–21.Google Scholar
Karanth, D., Rankin, G. W. & Sridhar, K. 1995 Computational study of flow past a cylinder with combined in-line and transverse oscillation. Comput. Mech. 16 (1), 1–10.Google Scholar
Kim, K., Baek, S. J. & Sung, H. J. 2002 An implicit velocity decoupling procedure for the incompressible Navier–Stokes equations. Intl J. Numer. Meth. Fluids 38 (2), 125–138.Google Scholar
Kim, W., Yoo, J. Y. & Sung, J. 2006 Dynamics of vortex lock-on in a perturbed cylinder wake. Phys. Fluids 18 (7), 074103.Google Scholar
Konstantinidis, E. & Balabani, S. 2007a Symmetric vortex shedding in the near wake of a circular cylinder due to streamwise perturbations. J. Fluids Struct. 23 (7), 1047–1063.Google Scholar
Konstantinidis, E. & Balabani, S. 2007b Symmetric vortex shedding in the near wake of a circular cylinder due to streamwise perturbations. J. Fluids Struct. 23 (7), 1047–1063.Google Scholar
Konstantinidis, E., Balabani, S. & Yianneskis, M. 2003 The effect of flow perturbations on the near wake characteristics of a circular cylinder. J. Fluids Struct. 18 (3), 367–386.Google Scholar
Konstantinidis, E., Balabani, S. & Yianneskis, M. 2005 The timing of vortex shedding in a cylinder wake imposed by periodic inflow perturbations. J. Fluid Mech. 543, 45–55.Google Scholar
Konstantinidis, E., Balabani, S. & Yianneskis, M. 2007 Bimodal vortex shedding in a perturbed cylinder wake. Phys. Fluids 19 (1), 011701.Google Scholar
Konstantinidis, E. & Bouris, D. 2016 Vortex synchronization in the cylinder wake due to harmonic and non-harmonic perturbations. J. Fluid Mech. 804, 248–277.Google Scholar
Koopmann, G. H. 1967 The vortex wakes of vibrating cylinders at low Reynolds numbers. J. Fluid Mech. 28 (03), 501–512.Google Scholar
Leontini, J. S., Jacono, D. L. & Thompson, M. C. 2011 A numerical study of an inline oscillating cylinder in a free stream. J. Fluid Mech. 688, 551–568.Google Scholar
Leontini, J. S., Jacono, D. L. & Thompson, M. C. 2013 Wake states and frequency selection of a streamwise oscillating cylinder. J. Fluid Mech. 730, 162–192.Google Scholar
Liu, C., Zheng, X. & Sung, C. H. 1998 Preconditioned multigrid methods for unsteady incompressible flows. J. Comput. Phys. 139 (1), 35–57.Google Scholar
Marzouk, O. A. & Nayfeh, A. H. 2009 Reduction of the loads on a cylinder undergoing harmonic in-line motion. Phys. Fluids 21 (8), 083103.Google Scholar
Morse, T. L. & Williamson, C. H. K. 2009 Prediction of vortex-induced vibration response by employing controlled motion. J. Fluid Mech. 634, 5–39.Google Scholar
Nishihara, T., Kaneko, S. & Watanabe, T. 2005 Characteristics of fluid dynamic forces acting on a circular cylinder oscillated in the streamwise direction and its wake patterns. J. Fluids Struct. 20 (4), 505–518.Google Scholar
Ongoren, A. & Rockwell, D. 1988 Flow structure from an oscillating cylinder. Part 1. Mechanisms of phase shift and recovery in the near wake. J. Fluid Mech. 191, 197–223.Google Scholar
Pan, X., Lee, C., Kim, K. & Choi, J.-I. 2016 Analysis of velocity-components decoupled projection method for the incompressible Navier–Stokes equations. Comput. Maths Appl. 71 (8), 1722–1743.Google Scholar
Park, J., Kwon, K. & Choi, H. 1998 Numerical solutions of flow past a circular cylinder at Reynolds numbers up to 160. J. Mech. Sci. Technol. 12 (6), 1200–1205.Google Scholar
Perdikaris, P. G., Kaiktsis, L. & Triantafyllou, G. S. 2009 Chaos in a cylinder wake due to forcing at the Strouhal frequency. Phys. Fluids 21 (10), 101705.Google Scholar
Qu, L., Norberg, C., Davidson, L., Peng, S.-H. & Wang, F. 2013 Quantitative numerical analysis of flow past a circular cylinder at Reynolds number between 50 and 200. J. Fluids Struct. 39, 347–370.Google Scholar
Tanida, Y., Okajima, A. & Watanabe, Y. 1973 Stability of a circular cylinder oscillating in uniform flow or in a wake. J. Fluid Mech. 61 (04), 769–784.Google Scholar
Wu, M.-H., Wen, C.-Y., Yen, R.-H., Weng, M.-C. & Wang, A.-B. 2004 Experimental and numerical study of the separation angle for flow around a circular cylinder at low Reynolds number. J. Fluid Mech. 515, 233–260.Google Scholar
Xu, S. J., Zhou, Y. u. & Wang, M. H. 2006 A symmetric binary-vortex street behind a longitudinally oscillating cylinder. J. Fluid Mech. 556, 27–43.Google Scholar
Yokoi, Y. & Kamemoto, K. 1994 Vortex shedding from an oscillating circular cylinder in a uniform flow. Exp. Therm. Fluid Sci. 8 (2), 121–127.Google Scholar