Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-12-01T11:38:39.710Z Has data issue: false hasContentIssue false
  • English
  • Français

Lock-exchange release density currents over three-dimensional regular roughness elements

Published online by Cambridge University Press:  30 October 2017

Kiran Bhaganagar Open the ORCID record for Kiran Bhaganagar [Opens in a new window]  and
Narasimha Rao Pillalamarri
Kiran Bhaganagar*
Affiliation:
Laboratory of Turbulence, Sensing and Intelligence Systems, Department of Mechanical Engineering, University of Texas at San Antonio, San Antonio, TX 78249, USA
Narasimha Rao Pillalamarri
Affiliation:
Laboratory of Turbulence, Sensing and Intelligence Systems, Department of Mechanical Engineering, University of Texas at San Antonio, San Antonio, TX 78249, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A fundamental study has been conducted to understand the front characteristics and the mixing in the flow of density currents over rough surfaces. A large-eddy simulation (LES) has been performed for lock-exchange release density currents over rough walls to shed light on the unsteady mixing processes. A volume-penalization method, which is a special case of the immersed-boundary method, has been implemented to realize the bottom-mounted rough topology. In this study, the LES has been conducted in a channel with a lower wall covered with three-dimensional cube- and pyramid-shaped roughness elements, such that all cases have the same base area, but differences in the roughness solidity and volume fraction of roughness. Both cases of identical roughness elements and those with randomness in height have been considered. The maximum roughness height for all cases is kept at a constant fraction (10 %) of the total channel height. The study focuses on the instantaneous mixing processes in lock-exchange release currents over rough surfaces. An important contribution of the work is that qualitative and quantitative analysis has been conducted to demonstrate additional mixing mechanisms due to the presence of surface roughness that enhances dilution of the current. 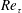Enhanced mixing due to roughness is related to the strength of the shear layer resulting from the roughness, and hence depends on friction Reynolds number ($Re_{\unicode[STIX]{x1D70F}}$). The combined role of current characteristics and 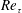$Re_{\unicode[STIX]{x1D70F}}$ together dictate the mixing processes and extent of dilution in density currents over surface roughness.

JFM classification

Geophysical and Geological Flows: Gravity currents Geophysical and Geological Flows: Topographic effects Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 832 , 10 December 2017 , pp. 793 - 824
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adduce, C., Lombardi, V., Sciortino, G. & Morganti, M. 2009 Roughness effects on gravity currents dynamics. In Proceedings of the 33rd IAHR Congress, Canada. International Association for Hydro-Environment Engineering and Research.Google Scholar
Angot, P., Bruneau, C.-H. & Fabrie, P. 1999 A penalization method to take into account obstacles in incompressible viscous flows. Numer. Math. 81 (4), 497–520.CrossRefGoogle Scholar
Anjum, H. J., McElwaine, J. N. & Caulfield, C.-C. P. 2013 The instantaneous Froude number and depth of unsteady gravity currents. J. Hydraul. Res. 51 (4), 432–445.CrossRefGoogle Scholar
Barr, D. I. H. 1963 Densimetric exchange flow in rectangular channels. I. Definitions, review and relevance to model design. La Houille Blanche 1 (7), 739–756.CrossRefGoogle Scholar
Benjamin, T. B. 1968 Gravity currents and related phenomena. J. Fluid Mech. 31 (02), 209–248.Google Scholar
Bhaganagar, K. 2014 Direct numerical simulation of lock-exchange density currents rough wall in slumping regime. J. Hydraul. Res. 52 (3), 386–393.Google Scholar
Bhaganagar, K. 2017 Role of head of turbulent 3-D density currents in mixing during slumping regime. Phys. Fluids 29 (2), 020703.CrossRefGoogle Scholar
Bhaganagar, K. & Chau, L. 2015 Characterizing turbulent flow over 3-D idealized and irregular rough surfaces at low Reynolds number. Appl. Math. Model. 39 (22), 6751–6766.CrossRefGoogle Scholar
Bhaganagar, K., Kim, J. & Coleman, G. 2004 Effect of roughness on wall-bounded turbulence. Flow Turbul. Combust. 72 (2), 463–492.CrossRefGoogle Scholar
Borden, Z. & Meiburg, E. 2013 Circulation based models for Boussinesq gravity currents. Phys. Fluids 25 (10), 101301.Google Scholar
Brinkman, H. C. 1949 On the permeability of media consisting of closely packed porous particles. Flow Turbul. Combust. 1 (1), 81.CrossRefGoogle Scholar
Britter, R. E. & Simpson, J. E. 1978 Experiments on the dynamics of a gravity current head. J. Fluid Mech. 88 (02), 223–240.CrossRefGoogle Scholar
Cantero, M. I., Balachandar, S., García, M. H. & Ferry, J. P. 2006 Direct numerical simulations of planar and cylindrical density currents. Trans. ASME J. Appl. Mech. 73 (6), 923–930.Google Scholar
Cenedese, C., Nokes, R. & Hyatt, J. 2017 Lock-exchange gravity currents over rough bottoms. Environ. Fluid Mech., doi:10.1007/s10652-016-9501-0.Google Scholar
Chau, L. & Bhaganagar, K. 2012 Understanding turbulent flow over ripple-shaped random roughness in a channel. Phys. Fluids 24 (11), 115102.CrossRefGoogle Scholar
Counehan, J. 1971 Wind tunnel determination of the roughness length as a function of the fetch and the roughness density of three-dimensional roughness elements. Atmos. Environ. 5 (8), 637–642.CrossRefGoogle Scholar
De Marchis, M. & Napoli, E. 2012 Effects of irregular two-dimensional and three-dimensional surface roughness in turbulent channel flows. Intl J. Heat Fluid Flow 36, 7–17.Google Scholar
Ergun, S. 1952 Fluid flow through packed columns. Chem. Engng Prog. 48, 89–94.Google Scholar
Fannelop, T. K. & Waldman, G. D. 1971 The dynamics of oil slicks – or ‘creeping crude’. In AIAA 9th Aerospace Sciences Meeting.Google Scholar
Fay, J. A. 1969 The spread of oil slicks on a calm sea. In Oil on the Sea, pp. 53–63. Springer.Google Scholar
Fernandez, R. L. & Imberger, J. 2006 Bed roughness induced entrainment in a high Richardson number underflow. J. Hydraul. Res. 44 (6), 725–738.CrossRefGoogle Scholar
Flack, K. A. & Schultz, M. P. 2014 Roughness effects on wall-bounded turbulent flows. Phys. Fluids 26 (10), 101305.Google Scholar
Forchheimer, P. 1901 Wasserbewegung durch boden. Z. Verein. Deutsch. Ing. 45 (1782), 1788.Google Scholar
Fragoso, A. T., Patterson, M. D. & Wettlaufer, J. S. 2013 Mixing in gravity currents. J. Fluid Mech. 734, R2.Google Scholar
Germano, M., Piomelli, U., Moin, P. & Cabot, W. H. 1991 A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A 3 (7), 1760–1765.Google Scholar
Goldstein, D., Handler, R. & Sirovich, L. 1993 Modeling a no-slip flow boundary with an external force field. J. Comput. Phys. 105 (2), 354–366.Google Scholar
Gonzalez-Juez, E., Meiburg, E. & Constantinescu, G. 2009 Gravity currents impinging on bottom-mounted square cylinders: flow fields and associated forces. J. Fluid Mech. 631, 65–102.Google Scholar
Gonzalez-Juez, E., Meiburg, E., Tokyay, T. & Constantinescu, G. 2010 Gravity current flow past a circular cylinder: forces, wall shear stresses and implications for scour. J. Fluid Mech. 649, 69–102.CrossRefGoogle Scholar
Hacker, J., Linden, P. F. & Dalziel, S. B. 1996 Mixing in lock-release gravity currents. Dyn. Atmos. Oceans 24 (1–4), 183–195.Google Scholar
Härtel, C., Meiburg, E. & Necker, F. 2000 Analysis and direct numerical simulation of the flow at a gravity-current head. Part 1. Flow topology and front speed for slip and no-slip boundaries. J. Fluid Mech. 418, 189–212.CrossRefGoogle Scholar
Hoult, D. P. 1972 Oil spreading on the sea. Annu. Rev. Fluid Mech. 4 (1), 341–368.Google Scholar
Hughes, G. O. & Linden, P. F. 2016 Mixing efficiency in run-down gravity currents. J. Fluid Mech. 809, 691–704.Google Scholar
Huppert, H. E. & Simpson, J. E. 1980 The slumping of gravity currents. J. Fluid Mech. 99 (04), 785–799.Google Scholar
Jimenez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.CrossRefGoogle Scholar
Keulegan, G. 1958 The motion of saline fronts in still water. Nat. Bur. Stand. Rep. 5813.Google Scholar
Kneller, B. C., Bennett, S. J. & McCaffrey, W. D. 1999 Velocity structure, turbulence and fluid stresses in experimental gravity currents. J. Geophys. Res. 104 (C3), 5381–5391.CrossRefGoogle Scholar
La Rocca, M., Adduce, C., Sciortino, G. & Pinzon, A. B. 2008 Experimental and numerical simulation of three-dimensional gravity currents on smooth and rough bottom. Phys. Fluids 20 (10), 106603.Google Scholar
Lettau, H. 1969 Note on aerodynamic roughness-parameter estimation on the basis of roughness-element description. J. Appl. Meteorol. 8 (5), 828–832.Google Scholar
Macdonald, R. W., Griffiths, R. F. & Hall, D. J. 1998 An improved method for the estimation of surface roughness of obstacle arrays. Atmos. Environ. 32 (11), 1857–1864.Google Scholar
McElwaine, J. N. 2005 Rotational flow in gravity current heads. Phil. Trans. R. Soc. Lond. A 363 (1832), 1603–1623.Google Scholar
Micard, D., Dossmann, Y., Gostiaux, L. & Venaille, A. 2016 Mixing efficiency in a lock exchange experiment. In VIIIth International Symposium on Stratified Flows, vol. 1. University of California.Google Scholar
Negretti, M. E., Zhu, D. Z. & Jirka, G. H. 2008 The effect of bottom roughness in two-layer flows down a slope. Dyn. Atmos. Oceans 45 (1), 46–68.Google Scholar
Nikuradse, J. 1933 Laws of Flow in Rough Pipes. VDI Forschungsheft.Google Scholar
Nogueira, H. I. S., Adduce, C., Alves, E. & Franca, M. J. 2014 Dynamics of the head of gravity currents. Environ. Fluid Mech. 14 (2), 519–540.Google Scholar
Orlandi, P. & Leonardi, S. 2004 Passive scalar in a turbulent channel flow with wall velocity disturbances. Flow Turbul. Combust. 72 (2), 181–197.CrossRefGoogle Scholar
Orlandi, P. & Leonardi, S. 2006 DNS of turbulent channel flows with two- and three-dimensional roughness. J. Turbul. 7, N73.Google Scholar
Ottolenghi, L., Adduce, C., Inghilesi, R., Armenio, V. & Roman, F. 2016 Entrainment and mixing in unsteady gravity currents. J. Hydraul. Res. 54 (5), 541–557.Google Scholar
Özgökmen, T. M. & Fischer, P. F. 2008 On the role of bottom roughness in overflows. Ocean Model. 20 (4), 336–361.CrossRefGoogle Scholar
Özgökmen, T. M., Iliescu, T. & Fischer, P. F. 2009 Large eddy simulation of stratified mixing in a three-dimensional lock-exchange system. Ocean Model. 26 (3), 134–155.CrossRefGoogle Scholar
Peters, W. D. & Venart, J. E. S. 2000 Visualization of rough-surface gravity current flows using laser-induced fluorescence. In 9th (Millennium) International Symposium on Flow Visualization.Google Scholar
Prastowo, T., Griffiths, R. W., Hughes, G. O. & Hogg, A. M. 2009 Effects of topography on the cumulative mixing efficiency in exchange flows. J. Geophys. Res. 114 (C8), C08008.Google Scholar
Rottman, J. W. & Simpson, J. E. 1983 Gravity currents produced by instantaneous releases of a heavy fluid in a rectangular channel. J. Fluid Mech. 135, 95–110.CrossRefGoogle Scholar
Samasiri, P. & Woods, A. W. 2015 Mixing in axisymmetric gravity currents. J. Fluid Mech. 782, R1.Google Scholar
Schlichting, H. 1936 Experimental investigation of the problem of surface roughness. Ingenieur-Archiv 7 (1), 1–34.Google Scholar
Schultz, M. P. & Flack, K. A. 2009 Turbulent boundary layers on a systematically varied rough wall. Phys. Fluids 21 (1), 015104.CrossRefGoogle Scholar
Shin, J. O., Dalziel, S. B. & Linden, P. F. 2004 Gravity currents produced by lock exchange. J. Fluid Mech. 521, 1–34.Google Scholar
Simpson, J. E. 1972 Effects of the lower boundary on the head of a gravity current. J. Fluid Mech. 53 (04), 759–768.Google Scholar
Simpson, J. E. 1982 Gravity currents in the laboratory, atmosphere, and ocean. Annu. Rev. Fluid Mech. 14 (1), 213–234.CrossRefGoogle Scholar
Simpson, J. E. & Britter, R. E. 1979 The dynamics of the head of a gravity current advancing over a horizontal surface. J. Fluid Mech. 94 (03), 477–495.Google Scholar
Tanino, Y. & Nepf, H. M. 2008 Laboratory investigation of mean drag in a random array of rigid, emergent cylinders. J. Hydraul. Engng 134 (1), 34–41.CrossRefGoogle Scholar
Tanino, Y., Nepf, H. M. & Kulis, P. S. 2005 Gravity currents in aquatic canopies. Water Resour. Res. 41 (12), W12402.Google Scholar
Thomas, L. P., Dalziel, S. B. & Marino, B. M. 2003 The structure of the head of an inertial gravity current determined by particle-tracking velocimetry. Exp. Fluids 34 (6), 708–716.Google Scholar
Tokyay, T. & Constantinescu, G. 2015 The effects of a submerged non-erodible triangular obstacle on bottom propagating gravity currents. Phys. Fluids 27 (5), 056601.Google Scholar
Tokyay, T., Constantinescu, G. & Meiburg, E. 2011 Lock-exchange gravity currents with a high volume of release propagating over a periodic array of obstacles. J. Fluid Mech. 672, 570–605.Google Scholar
Tokyay, T., Constantinescu, G. & Meiburg, E. 2012 Tail structure and bed friction velocity distribution of gravity currents propagating over an array of obstacles. J. Fluid Mech. 694, 252–291.Google Scholar
Wilson, R. I., Friedrich, H. & Stevens, C. 2017 Turbulent entrainment in sediment-laden flows interacting with an obstacle. Phys. Fluids 29 (3), 036603.Google Scholar
Winters, K. B., Lombard, P. N., Riley, J. J. & D’Asaro, E. A. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 289, 115–128.Google Scholar
Wu, Y. & Christensen, K. T. 2010 Spatial structure of a turbulent boundary layer with irregular surface roughness. J. Fluid Mech. 655, 380–418.Google Scholar
Yuksel Ozan, A., Constantinescu, G. & Hogg, A. J. 2015 Full-depth lock exchange gravity currents with a high volume of release propagating through arrays of cylinders. J. Fluid Mech. 675, 544–575.Google Scholar
Zgheib, N., Bonometti, T. & Balachandar, S. 2015 Propagation and deposition of non-circular finite release particle-laden currents. Phys. Fluids 27 (8), 086604.Google Scholar