Article contents
Localization of flow structures using 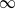 $\infty $-norm optimization
$\infty $-norm optimization
Published online by Cambridge University Press: 24 July 2013
Abstract
Stability theory based on a variational principle and finite-time direct-adjoint optimization commonly relies on the kinetic perturbation energy density 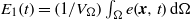 ${E}_{1} (t)= (1/ {V}_{\Omega } )\int \nolimits _{\Omega } e(\boldsymbol{x}, t)\hspace{0.167em} \mathrm{d} \Omega $ (where
${E}_{1} (t)= (1/ {V}_{\Omega } )\int \nolimits _{\Omega } e(\boldsymbol{x}, t)\hspace{0.167em} \mathrm{d} \Omega $ (where 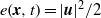 $e(\boldsymbol{x}, t)= \vert \boldsymbol{u}{\vert }^{2} / 2$) as a measure of disturbance size. This type of optimization typically yields optimal perturbations that are global in the fluid domain
$e(\boldsymbol{x}, t)= \vert \boldsymbol{u}{\vert }^{2} / 2$) as a measure of disturbance size. This type of optimization typically yields optimal perturbations that are global in the fluid domain 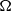 $\Omega $ of volume
$\Omega $ of volume 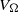 ${V}_{\Omega } $. This paper explores the use of
${V}_{\Omega } $. This paper explores the use of 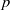 $p$-norms in determining optimal perturbations for ‘energy’ growth over prescribed time intervals of length
$p$-norms in determining optimal perturbations for ‘energy’ growth over prescribed time intervals of length 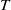 $T$. For
$T$. For 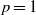 $p= 1$ the traditional energy-based stability analysis is recovered, while for large
$p= 1$ the traditional energy-based stability analysis is recovered, while for large  $p\gg 1$, localization of the optimal perturbations is observed which identifies confined regions, or ‘hotspots’, in the domain where significant energy growth can be expected. In addition, the
$p\gg 1$, localization of the optimal perturbations is observed which identifies confined regions, or ‘hotspots’, in the domain where significant energy growth can be expected. In addition, the 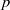 $p$-norm optimization yields insight into the role and significance of various regions of the flow regarding the overall energy dynamics. As a canonical example, we choose to solve the
$p$-norm optimization yields insight into the role and significance of various regions of the flow regarding the overall energy dynamics. As a canonical example, we choose to solve the 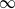 $\infty $-norm optimal perturbation problem for the simple case of two-dimensional channel flow. For such a configuration, several solutions branches emerge, each of them identifying a different energy production zone in the flow: either the centre or the walls of the domain. We study several scenarios (involving centre or wall perturbations) leading to localized energy production for different optimization time intervals. Our investigation reveals that even for this simple two-dimensional channel flow, the mechanism for the production of a highly energetic and localized perturbation is not unique in time. We show that wall perturbations are optimal (with respect to the
$\infty $-norm optimal perturbation problem for the simple case of two-dimensional channel flow. For such a configuration, several solutions branches emerge, each of them identifying a different energy production zone in the flow: either the centre or the walls of the domain. We study several scenarios (involving centre or wall perturbations) leading to localized energy production for different optimization time intervals. Our investigation reveals that even for this simple two-dimensional channel flow, the mechanism for the production of a highly energetic and localized perturbation is not unique in time. We show that wall perturbations are optimal (with respect to the 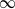 $\infty $-norm) for relatively short and long times, while the centre perturbations are preferred for very short and intermediate times. The developed
$\infty $-norm) for relatively short and long times, while the centre perturbations are preferred for very short and intermediate times. The developed 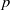 $p$-norm framework is intended to facilitate worst-case analysis of shear flows and to identify localized regions supporting dominant energy growth.
$p$-norm framework is intended to facilitate worst-case analysis of shear flows and to identify localized regions supporting dominant energy growth.
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 34
- Cited by


