Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T14:29:52.164Z Has data issue: false hasContentIssue false
  • English
  • Français

A local scattering theory for the effects of isolated roughness on boundary-layer instability and transition: transmission coefficient as an eigenvalue

Published online by Cambridge University Press:  30 March 2016

Xuesong Wu  and
Ming Dong
Xuesong Wu*
Affiliation:
Department of Mathematics, Imperial College London, 180 Queen’s Gate, London SW7 2AZ, UK
Ming Dong
Affiliation:
Department of Mechanics, Tianjin University, Tianjin 300072, PR China Tianjin Key Laboratory of Modern Engineering Mechanics, Tianjin 300072, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is concerned with the rather broad issue of the impact of abrupt changes (such as isolated roughness, gaps and local suctions) on boundary-layer transition. To fix the idea, we consider the influence of a two-dimensional localized hump (or indentation) on an oncoming Tollmien–Schlichting (T–S) wave. We show that when the length scale of the former is comparable with the characteristic wavelength of the latter, the key physical mechanism to affect transition is through scattering of T–S waves by the roughness-induced mean-flow distortion. An appropriate mathematical theory, consisting of the boundary-value problem governing the local scattering, is formulated based on triple deck formalism. The transmission coefficient, defined as the ratio of the amplitude of the T–S wave downstream of the roughness to that upstream, serves to characterize the impact on transition. The transmission coefficient appears as the eigenvalue of the discretized boundary-value problem. The latter is solved numerically, and the dependence of the eigenvalue on the height and width of the roughness and the frequency of the T–S wave is investigated. For a roughness element without causing separation, the transmission coefficient is found to be approximately 1.5 for typical frequencies, indicating a moderate but appreciable destabilizing effect. For a roughness causing incipient separation, the transmission coefficient can be as large as 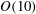$O(10)$, suggesting that immediate transition may take place at the roughness site. A roughness element with a fixed height produces the strongest impact when its width is comparable with the T–S wavelength, in which case the traditional linear stability theory is invalid. The latter however holds approximately when the roughness width is sufficiently large. By studying the two hump case, a criterion when two roughness elements can be regarded as being isolated is suggested. The transmission coefficient can be converted to an equivalent 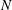$N$-factor increment, by making use of which the 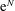$\text{e}^{N}$-method can be extended to predict transition in the presence of multiple roughness elements.

JFM classification

Boundary Layers: Boundary layer stability Instability: Transition to turbulence Waves/Free-surface Flows: Wave scattering
Type
Papers
Information
Journal of Fluid Mechanics , Volume 794 , 10 May 2016 , pp. 68 - 108
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asai, M., Minagawa, M. & Nishioka, M. 2002 The instability and breakdown of a near-wall low-speed streak. J. Fluid Mech. 455, 289–314.Google Scholar
Bodonyi, R. J. & Duck, P. W. 1988 A numerical method for treating strongly interactive three-dimensional viscous-inviscid flows. Comput. Fluids 16, 279–290.CrossRefGoogle Scholar
Bodonyi, R. J., Welch, W. J. C., Duck, P. W. & Tadjfar, M. 1989 A numerical study of the interaction between unsteady free-stream disturbances and localized variations in surface geometry. J. Fluid Mech. 209, 285–308.Google Scholar
Carmichael, B. H.1959 Surface waviness criteria for swept and unswept laminar suction wings. Northrop Corp. Report No. NOR-59-438 (BLC-123).Google Scholar
Cebeci, T. & Egan, D. A. 1989 Prediction of transition due to isolated roughness. AIAA J. 27, 870–875.Google Scholar
Choudhari, M., Li, F. & Edwards, J.2009 Stability analysis of roughness array wake in a high speed boundary layer. AIAA Paper 2009-0170.Google Scholar
Choudhari, M., Norris, A., Li, F., Chang, C. L. & Edwards, J.2013 Wake instabilities behind discrete roughness elements in high-speed boundary layers. AIAA Paper 2013-0081.Google Scholar
Corke, T. C., Barsever, A. & Morkovin, M. V. 1986 Experiments on transition enhancement by distributed roughness. Phys. Fluids 29, 3199–3213.CrossRefGoogle Scholar
Crouch, J. D., Kosorygin, V. S. & Ng, L. L. 2006 Modelling the effecs of steps on boundary-layer transition. In Sixth IUTAM Symposium on Laminar–Turbulent Transition (ed. Govindarajan, R.), Springer.Google Scholar
De Tullio, N., Paredes, P., Sandham, N. D. & Theofilis, V. 2013 Laminar–turbulent transition induced by a discrete roughness element in a supersonic boundary layer. J. Fluid Mech. 735, 613–646.Google Scholar
Duck, P. W., Ruban, A. I. & Zhikharev, C. N. 1996 The generation of Tollmien–Schlichting waves by free-stream turbulence. J. Fluid Mech. 312, 341–371.Google Scholar
Edelmann, C. A. & Rist, U.2013 Impact of forward-facing steps on laminar–turbulent transition in transonic flows without pressure gradient. AIAA Paper 2013-0080.Google Scholar
El-Mistikawy, T. 1994 Efficient solution of Keller’s box equations for direct and inverse boundary layer equations. AIAA J. 32, 1538–1541.Google Scholar
El-Mistikawy, T. 2010 Subsonic triple deck flow past a flat plate with an elastic stretch. Appl. Math. Model. 34, 1238–1246.CrossRefGoogle Scholar
Fage, A.1943 The smallest size of spanwise surface corrugation which affects boundary layer transtion on an airfoil. British Aeronautical Research Council Report No. 2120.Google Scholar
Fedorov, A. V. 2011 Transition and stability of high-speed boundary layers. Annu. Rev. Fluid Mech. 43, 79–95.Google Scholar
Fong, K. D., Wang, X. & Zhong, X.2013 Stabilization of hypersonic boundary layer by 2-D surface roughness. AIAA Paper 2013-2985.Google Scholar
Fransson, J. H. M., Brandt, L., Talamelli, A. & Cossu, C. 2005 Experimental study of the stabilization of Tollmien–Schlichting waves by finite amplitude streaks. Phys. Fluids 17, 054110-1.Google Scholar
Fujii, K. 2006 Experiment of the two-dimensional roughness effect on hypersonic boundary-layer transition. J. Spacecr. Rockets 43, 731–738.CrossRefGoogle Scholar
Goldstein, M. E. 1985 Scattering of acoustic waves into Tollmien–Schlichting waves by small streamwise variations in surface geometry. J. Fluid Mech. 154, 509–530.Google Scholar
Goldstein, M. E. & Hultgren, L. S. 1989 Boundary-layer receptivity to long-wave free-stream disturbances. Annu. Rev. Fluid Mech. 21, 137–166.Google Scholar
Iyer, P. S., Muppidi, S. & Mahesh, K.2011 Roughness-induced transition in high-speed flows. AIAA Paper 2004-0589.Google Scholar
Kachanov, Y. S. 1994 Physical mechanisms of laminar-boundary-layer transition. Annu. Rev. Fluid Mech. 26, 411–482.Google Scholar
Kegerise, M. A., Owen, L. R. & Rudolf, A. K.2010 High-speed boundary-layer transition induced by an isolated roughness element. AIAA Paper 2010-4999.Google Scholar
Klebanoff, P. S. & Tidstrom, K. D. 1972 Mechanism by which a two-dimensional roughness element induces boundary-layer transition. Phys. Fluids 15, 1172–1188.Google Scholar
Mack, L. M.1984 Boundary layer linear stability theory. AGARD Rep., pp. 3-1–3-81.Google Scholar
Malik, M.1990 Finite difference solution of the compressible stability eigenvalue problem. NASA Tech. Rep. 16572.Google Scholar
Ma’mun, M. D., Asai, M. & Inasawa, A. 2014 Effects of surface corrugation on the stability of a zero-pressure-gradient boundary layer. J. Fluid Mech. 741, 228–251.Google Scholar
Marxen, O., Iaccarino, G. & Shaqfeh, E. S. G. 2010 Disturbance evolution in a Mach 4.8 boundary layer with two-dimensional roughness-induced separation and shock. J. Fluid Mech. 648, 435–469.CrossRefGoogle Scholar
Masad, J. A. 1995 Transition in flow over heat transfer strips. Phys. Fluids 7, 2163–2174.Google Scholar
Masad, J. A. & Iyer, V. 1994 Transition prediction and control in subsonc flow over a hump. Phys. Fluids 6, 313–327.Google Scholar
Masad, J. A. & Nayfeh, A. H. 1992 Laminar flow control of subsonic boundary layers by suction and heat transfer strips. Phys. Fluids 4, 1259–1272.Google Scholar
Nayfeh, A. H. & Abu-Khajeel, H. T. 1996 Effect of a hump on the stability of subsonic boundary layers over an airfoil. Intl J. Engng Sci. 34, 599–628.CrossRefGoogle Scholar
Nayfeh, A. H., Ragab, S. A. & Almaaitah, A. A. 1988 Effect of bulges on the stability of boundary layers. Phys. Fluids 31, 796–806.CrossRefGoogle Scholar
Nayfeh, A. H. & Reed, H. L. 1985 Stability of flow over axisymmetric bodies with porous suction strips. Phys. Fluids 28, 2990–2998.Google Scholar
Nayfeh, A. H., Reed, H. L. & Ragab, S. A. 1986 Flow over bodies with suction through porous strips. Phys. Fluids 29, 2042–2053.Google Scholar
Park, D. & Park, S. O. 2013 Linear and non-linear stability analysis of incompressible boundary layer over a two-dimensional hump. Comput. Fluids 73, 80–96.Google Scholar
Perraud, J., Arnal, D. & Kuehn, W. 2014 Laminar–turbulent transition prediction in the presence of surface imperfections. Intl J. Engng Syst. Model. Simul. 6, 162–170.Google Scholar
Perraud, J., Arnal, D., Seraudie, A. & Tran, D.2004 Laminar–turbulent transition on aerodynamic surfaces with imperfections. RTO-AVT-111 Symp., Prague.Google Scholar
Reed, H. L. & Nayfeh, A. H. 1986 Numerical-perturbation technique for stability of flat-plate boundary layers with suction. AIAA J. 24, 208–214.Google Scholar
Reed, H. L, Saric, W. S. & Arnal, D. 1996 Linear stability theory applied to boundary layers. Annu. Rev. Fluid Mech. 28, 389–428.Google Scholar
Reynolds, G. A. & Saric, W. S. 1986 Experiments on the stability of the flat-plate boundary layer with suction. AIAA J. 24, 202–207.Google Scholar
Ruban, A. I.1984 On Tollimien–Schlichting wave generation by sound (in Russian). Izv. Akad. Nauk SSSR Mekh. Zhidk. Gaza, No. 5, 44–52 (translation in Fluid Dyn. 19, 709–716).Google Scholar
Saric, W. S., Reed, H. L. & Kerschen, E. J. 2002 Boundary-layer receptivity to freestream disturbances. Annu. Rev. Fluid Mech. 34, 291–319.Google Scholar
Saric, W. S., Reed, H. L. & White, E. B. 2003 Stability and transition of three-dimensional boundary layers. Annu. Rev. Fluid Mech. 35, 413–440.CrossRefGoogle Scholar
Shahinfar, S. S. S., Sattarzadeh, S. S. & Fransson, J. H. M. 2014 Passive boundary layer control of oblique disturbances by finite-amplitude streaks. J. Fluid Mech. 749, 1–36.Google Scholar
Smith, F. T. 1973 Laminar flow over a small hump on flat plate. J. Fluid Mech. 57, 803–824.CrossRefGoogle Scholar
Smith, F. T. 1979 On the non-parallel flow stability of the Blasius boundary layer. Proc. R. Soc. Lond. A 366, 91–109.Google Scholar
Smith, F. T. 1989 On the first-mode instability in subsonic, supersonic or hypersonic boundary layers. J. Fluid Mech. 198, 127–153.Google Scholar
Stewartson, K. 1974 Multistructured boundary layers on flat plates and related bodies. Adv. Appl. Mech. 14, 145–239.Google Scholar
Theofilis, V. 2003 Advances in global linear instability analysis of non-parallel and three-dimensional flows. Prog. Aerosp. Sci. 39, 249–315.Google Scholar
Wang, Y. X. & Gaster, M. 2005 Effect of surface steps on boundary layer transition. Exp. Fluids 39, 679–686.Google Scholar
Wheaton, B. M. & Schneider, S. P. 2012 Roughness-induced instability in a hypersonic laminar boundary layer. AIAA J. 5 (6), 1245–1256.CrossRefGoogle Scholar
Wheaton, B. M. & Schneider, S. P.2013 Instability and transition due to near-critical roughness in a hypersonic laminar boundary layer. AIAA Paper 2013-0084.Google Scholar
Wie, Y. & Malik, M. R. 1998 Effect of surface waviness on boundary-layer transition in two-dimensional flow. Comput. Fluids 27, 157–181.Google Scholar
Wörner, A., Rist, U. & Wagner, S. 2003 Humps/steps influence on stability characteristics of two-dimensional laminar boundary layer. AIAA J. 41, 192–197.Google Scholar
Wu, X. 2001a On local boundary-layer receptivity to vortical disturbances in the free stream. J. Fluid Mech. 449, 373–393.Google Scholar
Wu, X. 2001b Receptivity of boundary layers with distributed roughness to vortical and acoustic disturbances: a second-order asymptotic theory and comparison with experiments. J. Fluid Mech. 431, 91–133.Google Scholar
Wu, X. & Hogg, L. 2006 Acoustic radiation of Tollmien–Schlichting waves as they undergo rapid distortion. J. Fluid Mech. 550, 307–347.Google Scholar
Wu, X. & Luo, J. 2003 Linear and nonlinear instabilities of a Blasius boundary layer perturbed by streamwise vortices. Part 1. Steady streaks. J. Fluid Mech. 483, 225–248.Google Scholar