Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T07:06:25.019Z Has data issue: false hasContentIssue false
  • English
  • Français

Local dissipation scales and energy dissipation-rate moments in channel flow

Published online by Cambridge University Press:  10 May 2012

P. E. Hamlington ,
D. Krasnov ,
T. Boeck  and
J. Schumacher
P. E. Hamlington
Affiliation:
Department of Aerospace Engineering Sciences, University of Colorado, Boulder, CO 80309-0429, USA
D. Krasnov
Affiliation:
Institut für Thermo- und Fluiddynamik, Technische Universität Ilmenau, Postfach 100565, D-98684 Ilmenau, Germany
T. Boeck
Affiliation:
Institut für Thermo- und Fluiddynamik, Technische Universität Ilmenau, Postfach 100565, D-98684 Ilmenau, Germany
J. Schumacher*
Affiliation:
Institut für Thermo- und Fluiddynamik, Technische Universität Ilmenau, Postfach 100565, D-98684 Ilmenau, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

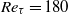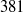Local dissipation-scale distributions and high-order statistics of the energy dissipation rate are examined in turbulent channel flow using very high-resolution direct numerical simulations at Reynolds numbers , and 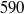. For sufficiently large 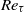, the dissipation-scale distributions and energy dissipation moments in the channel bulk flow agree with those in homogeneous isotropic turbulence, including only a weak Reynolds-number dependence of both the finest and largest scales. Systematic, but 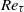-independent, variations in the distributions and moments arise as the wall is approached for 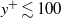. In the range 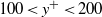, there are substantial differences in the moments between the lowest and the two larger values of 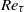. This is most likely caused by coherent vortices from the near-wall region, which fill the whole channel for low .

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulence theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 701 , 25 June 2012 , pp. 419 - 429
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Abe, H. & Antonia, R. A. 2011 Scaling of normalized mean energy and scalar dissipation rates in a turbulent channel flow. Phys. Fluids 23, 055104.CrossRefGoogle Scholar
2. Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.CrossRefGoogle Scholar
3. Bailey, S. C. C., Hultmark, M., Schumacher, J., Yakhot, V. & Smits, A. J. 2009 Measurement of dissipation scales in turbulent pipe flow. Phys. Rev. Lett. 103, 014502.CrossRefGoogle ScholarPubMed
4. Biferale, L. 2008 A note on the fluctuation of dissipative scale in turbulence. Phys. Fluids 20, 031703.CrossRefGoogle Scholar
5. Boeck, T., Krasnov, D. & Schumacher, J. 2010 Statistics of velocity gradients in wall-bounded shear flow turbulence. Physica D 239, 1258–1263.CrossRefGoogle Scholar
6. Donzis, D. A., Yeung, P. K. & Sreenivasan, K. R. 2008 Dissipation and enstrophy in isotropic turbulence: resolution effects and scaling in direct numerical simulations. Phys. Fluids 20, 045108.CrossRefGoogle Scholar
7. Garcia, C. M., Jackson, P. R. & Garcia, M. H. 2005 Confidence intervals in the determination of turbulence parameters. Exp. Fluids 40, 514–522.CrossRefGoogle Scholar
8. Hamlington, P. E., Krasnov, D., Boeck, T. & Schumacher, J. 2012 Statistics of energy dissipation rate and local enstrophy in turbulent channel flow. Physica D 241, 169–177.CrossRefGoogle Scholar
9. Hoyas, S. & Jimenez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to . Phys. Fluids 18, 011702.CrossRefGoogle Scholar
10. Ishihara, T., Gotoh, T. & Kaneda, Y. 2009 Study of high-Reynolds number isotropic turbulence by direct numerical simulation. Annu. Rev. Fluid Mech. 41, 165–180.CrossRefGoogle Scholar
11. Kim, J., Moin, P. & Moser, R. D. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
12. Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible fluid for very large Reynolds number. Dokl. Akad. Nauk SSSR 30, 299–303.Google Scholar
13. Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to . Phys. Fluids 11, 943–945.CrossRefGoogle Scholar
14. Nelkin, M. 1990 Multifractal scaling of velocity derivatives in turbulence. Phys. Rev. A 42, 7226–7229.CrossRefGoogle ScholarPubMed
15. Paladin, G. & Vulpiani, A. 1987 Degrees of freedom of turbulence. Phys. Rev. A 35, 1971–1973.CrossRefGoogle ScholarPubMed
16. Schumacher, J. 2007 Sub-Kolmogorov scale fluctuations in fluid turbulence. Europhys. Lett. 80, 54001.CrossRefGoogle Scholar
17. Schumacher, J., Sreenivasan, K. R. & Yakhot, V. 2007 Asymptotic exponents from low-Reynolds number flows. New J. Phys. 9, 89.CrossRefGoogle Scholar
18. Schumacher, J., Sreenivasan, K. R. & Yeung, P. K. 2005 Very fine structures in scalar mixing. J. Fluid Mech. 531, 113–122.CrossRefGoogle Scholar
19. She, Z. S. & Lévêque, E. 1994 Universal scaling laws in fully developed turbulence. Phys. Rev. Lett. 72, 336–339.CrossRefGoogle ScholarPubMed
20. Sreenivasan, K. R. 2004 Possible effects of small-scale intermittency in turbulent reacting flows. Flow Turbul. Combust. 72, 115–131.CrossRefGoogle Scholar
21. Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.CrossRefGoogle Scholar
22. Wallace, J. M. & Vukoslavcević, P. V. 2010 Measurement of the velocity gradient tensor in turbulent flows. Annu. Rev. Fluid Mech. 42, 157–181.CrossRefGoogle Scholar
23. Yakhot, V. 2006 Probability densities in strong turbulence. Physica D 215, 166–174.CrossRefGoogle Scholar
24. Yakhot, V. & Sreenivasan, K. R. 2005 Anomalous scaling of structure functions and dynamic constraints on turbulence simulations. J. Stat. Phys. 121 (5), 823–841.CrossRefGoogle Scholar
25. Zhou, Q. & Xia, K.-Q. 2010 Universality of local dissipation scales in buoyancy-driven turbulence. Phys. Rev. Lett. 104, 124301.CrossRefGoogle ScholarPubMed