Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Tammisola, Outi
Lundell, Fredrik
and
Söderberg, L. Daniel
2012.
Surface tension-induced global instability of planar jets and wakes.
Journal of Fluid Mechanics,
Vol. 713,
Issue. ,
p.
632.
Tammisola, Outi
2012.
Oscillatory sensitivity patterns for global modes in wakes.
Journal of Fluid Mechanics,
Vol. 701,
Issue. ,
p.
251.
Emerson, Benjamin
O’Connor, Jacqueline
Juniper, Matthew
and
Lieuwen, Tim
2012.
Density ratio effects on reacting bluff-body flow field characteristics.
Journal of Fluid Mechanics,
Vol. 706,
Issue. ,
p.
219.
Camarri, Simone
Fallenius, Bengt E. G.
and
Fransson, Jens H. M.
2013.
Stability analysis of experimental flow fields behind a porous cylinder for the investigation of the large-scale wake vortices.
Journal of Fluid Mechanics,
Vol. 715,
Issue. ,
p.
499.
Iungo, G. V.
Viola, F.
Camarri, S.
Porté-Agel, F.
and
Gallaire, F.
2013.
Linear stability analysis of wind turbine wakes performed on wind tunnel measurements.
Journal of Fluid Mechanics,
Vol. 737,
Issue. ,
p.
499.
Fuster, D.
Matas, J.-P.
Marty, S.
Popinet, S.
Hoepffner, J.
Cartellier, A.
and
Zaleski, S.
2013.
Instability regimes in the primary breakup region of planar coflowing sheets.
Journal of Fluid Mechanics,
Vol. 736,
Issue. ,
p.
150.
Emerson, Benjamin
Mondragon, Ulises
Acharya, Vishal
Shin, Dong-Hyuk
Brown, Christopher
McDonell, Vincent
and
Lieuwen, Timothy
2013.
Velocity and Flame Wrinkling Characteristics of a Transversely Forced, Bluff-Body Stabilized Flame, Part I: Experiments and Data Analysis.
Combustion Science and Technology,
Vol. 185,
Issue. 7,
p.
1056.
Qadri, Ubaid Ali
Mistry, Dhiren
and
Juniper, Matthew P.
2013.
Structural sensitivity of spiral vortex breakdown.
Journal of Fluid Mechanics,
Vol. 720,
Issue. ,
p.
558.
Rodríguez, Daniel
Gennaro, Elmer M.
and
Juniper, Matthew P.
2013.
The two classes of primary modal instability in laminar separation bubbles.
Journal of Fluid Mechanics,
Vol. 734,
Issue. ,
Rodriguez, Daniel
Gennaro, Elmer M.
and
Juniper, Matthew P.
2013.
On the two classes of global primary modal instability in laminar separation bubbles.
Oberleithner, Kilian
Terhaar, Steffen
Rukes, Lothar
and
Oliver Paschereit, Christian
2013.
Why Nonuniform Density Suppresses the Precessing Vortex Core.
Journal of Engineering for Gas Turbines and Power,
Vol. 135,
Issue. 12,
Oberleithner, K.
Paschereit, C. O.
and
Wygnanski, I.
2014.
On the impact of swirl on the growth of coherent structures.
Journal of Fluid Mechanics,
Vol. 741,
Issue. ,
p.
156.
Ray, Prasun K.
and
Zaki, Tamer A.
2014.
Absolute instability in viscoelastic mixing layers.
Physics of Fluids,
Vol. 26,
Issue. 1,
PASCHEREIT, Christian Oliver
TERHAAR, Steffen
ĆOSIĆ, Bernhard
and
OBERLEITHNER, Kilian
2014.
Application of linear hydrodynamic stability analysis to reacting swirling combustor flows.
Journal of Fluid Science and Technology,
Vol. 9,
Issue. 3,
p.
JFST0024.
Oberleithner, Kilian
Rukes, Lothar
and
Soria, Julio
2014.
Mean flow stability analysis of oscillating jet experiments.
Journal of Fluid Mechanics,
Vol. 757,
Issue. ,
p.
1.
Tammisola, O.
Giannetti, F.
Citro, V.
and
Juniper, M. P.
2014.
Second-order perturbation of global modes and implications for spanwise wavy actuation.
Journal of Fluid Mechanics,
Vol. 755,
Issue. ,
p.
314.
Ray, Prasun K.
and
Zaki, Tamer A.
2015.
Absolute/convective instability of planar viscoelastic jets.
Physics of Fluids,
Vol. 27,
Issue. 1,
Qadri, Ubaid Ali
Chandler, Gary J.
and
Juniper, Matthew P.
2015.
Self-sustained hydrodynamic oscillations in lifted jet diffusion flames: origin and control.
Journal of Fluid Mechanics,
Vol. 775,
Issue. ,
p.
201.
Camarri, Simone
2015.
Flow control design inspired by linear stability analysis.
Acta Mechanica,
Vol. 226,
Issue. 4,
p.
979.
Emerson, Benjamin L.
Jagtap, Swapnil
and
Lieuwen, Tim C.
2015.
Stability Analysis of Reacting Wakes: Flow and Density Asymmetry Effects.
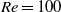 to determine the effect of confinement. We find that confinement acts in three ways: it modifies the length of the recirculation zone if one exists, it brings the boundary layers closer to the shear layers, and it can make the flow more locally absolutely unstable. Depending on the flow parameters, these effects work with or against each other to destabilize or stabilize the flow. In wake flows at
to determine the effect of confinement. We find that confinement acts in three ways: it modifies the length of the recirculation zone if one exists, it brings the boundary layers closer to the shear layers, and it can make the flow more locally absolutely unstable. Depending on the flow parameters, these effects work with or against each other to destabilize or stabilize the flow. In wake flows at 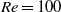 with free-slip boundaries, flows are most globally unstable when the outer flows are 50 % wider than the half-width of the inner flow because the first and third effects work together. In wake flows at
with free-slip boundaries, flows are most globally unstable when the outer flows are 50 % wider than the half-width of the inner flow because the first and third effects work together. In wake flows at 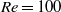 with no-slip boundaries, confinement has little overall effect when the flows are weakly confined because the first two effects work against the third. Confinement has a strong stabilizing effect, however, when the flows are strongly confined because all three effects work together. By combining local and global analyses, we have been able to isolate these three effects and resolve the apparent contradictions in previous work.
with no-slip boundaries, confinement has little overall effect when the flows are weakly confined because the first two effects work against the third. Confinement has a strong stabilizing effect, however, when the flows are strongly confined because all three effects work together. By combining local and global analyses, we have been able to isolate these three effects and resolve the apparent contradictions in previous work.

